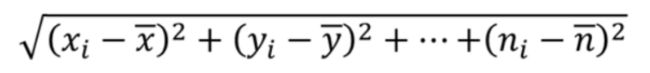【多目标跟踪与计数】（二）SORT原理与实战

前言

SORT论文地址：http://arxiv.org/pdf/1602.00763.pdf

本次项目源码地址：https://github.com/mikel-brostrom/Yolov5_DeepSort_Pytorch/tree/master/deep_sort_pytorch/deep_sort/sort

在介绍DeepSORT之前，需要引入SORT算法，其主要作用是第一次将CNN检测功能引入跟踪任务中，与以往的传统跟踪算法相比，追踪器的跟踪频率能够达到260Hz，比当时最新的追踪器快20倍；

DeepSORT算法本质上是对SORT的优化和拓展，从本次项目架构中可以看出，在deep_sort目录下，包含有sort和deep两个文件夹，而sort文件夹内部就是引用SORT算法进行如距离度量、卡尔曼滤波和最优分配等任务的实现；本篇将结合项目中的源码以及一些算法定义对SORT进行讲解；

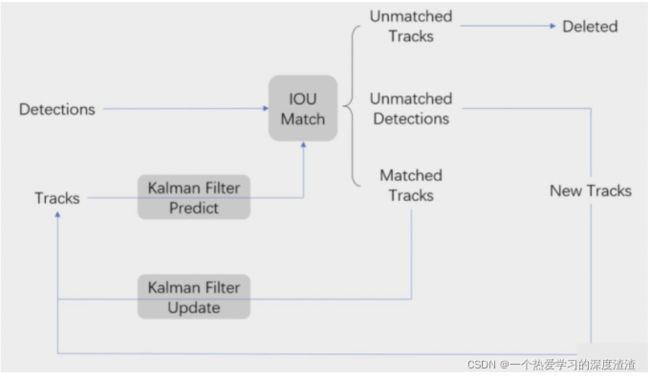
SORT的实现流程图：

数据关联流程讲解

多目标跟踪的实现方式一般为Tracking By Detecting，主要有以下两个步骤：

① 使用目标检测算法对每一帧中感兴趣的目标检测出来，得到相应的（检测框、分类、置信度），假设检测到的数量为M；

② 通过一定方式将步骤一检测的结果与上一帧检测的结果关联起来，假设上一帧检测的目标数量为N，那就是在M*N个匹配对中找出最匹配的组合；

检测算法：YOLOV5（上一篇文章讲解）

数据关联方法：常用的方法有两种，一是计算前后帧帧中两个目标的平面距离，二是计算前后帧的IOU占比，证明两帧检测的是同一目标即可关联起来；

如果单单用IOU做关联，可能存在以下问题：

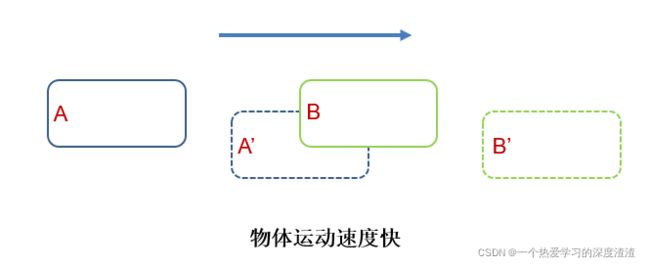
如上图所示，当物体运动过快时，两帧的运动轨迹不能够关联起来，此时用IOU的话会发生关联错误；

所以引入了一个概念，基于轨迹预测的跟踪方式：在目标检测后加入卡尔曼滤波预测下一帧的轨迹状态，如下图所示；

此时关联的就是卡尔曼滤波器预测后的结果与当前帧检测结果，不会出现速度过快匹配失败的问题；

距离度量

1、欧式距离

在介绍马氏距离之前，引入一种距离的度量方式：

上述公式相信大家都有接触过，通常计算两点的距离就是用该公式，计算的距离也称欧式距离；

缺点：并不考虑数据的分布情况，在一定情况下这种计算方式并不可靠；

代码实现在nn_matching.py中：

# 计算两个矩阵的欧式距离
def _pdist(a, b):
    # 用于计算成对的平方距离
    # a NxM 代表N个对象，每个对象有M个数值作为embedding进行比较
    # b LxM 代表L个对象，每个对象有M个数值作为embedding进行比较
    # 返回的是NxL的矩阵，比如dist[i][j]代表a[i]和b[j]之间的平方和距离
    a, b = np.asarray(a), np.asarray(b)
    if len(a) == 0 or len(b) == 0:
        return np.zeros((len(a), len(b)))
    a2, b2 = np.square(a).sum(axis=1), np.square(b).sum(axis=1)		# 求每个embedding的平方和
    r2 = -2. * np.dot(a, b.T) + a2[:, None] + b2[None, :]
    r2 = np.clip(r2, 0., float(np.inf))
    return r2

# 对欧式距离求最近邻距离
def _nn_euclidean_distance(x, y):
    distances = _pdist(x, y)
    return np.maximum(0.0, distances.min(axis=0))

对于计算公式的理解，可以参考文章：https://blog.csdn.net/frankzd/article/details/80251042

2、余弦距离

定义：余弦距离是通过余弦相似度得到的，对于两个向量的余弦相似度也就是夹角的cos值是很容易得到的，通过1-余弦值得到得结果为余弦距离；因为余弦相似度的取值范围为[-1，1]，那么余弦距离的取值范围为[0，2]；

对于两个向量（x1，y1）和（x2，y2）的余弦值计算公式如下：

余弦相似度的计算为：1 - cosθ即可得到；

代码实现在nn_matching.py中：

# 余弦距离的计算
def _cosine_distance(a, b, data_is_normalized=False):
    if not data_is_normalized:
        a = np.asarray(a) / np.linalg.norm(a, axis=1, keepdims=True)
        b = np.asarray(b) / np.linalg.norm(b, axis=1, keepdims=True)
    return 1. - np.dot(a, b.T)

# 对余弦距离求最近邻距离
def _nn_cosine_distance(x, y):
    distances = _cosine_distance(x, y)
    return distances.min(axis=0)

参考文章：https://blog.csdn.net/u013749540/article/details/51813922

3、马氏距离

定义：度量学习中一种常用的距离指标，与欧式距离不同的点在于，考虑到各种特性之间的联系（例如一条身高的信息会带来一条关于体重的信息，因为二者有关联），并且是尺度无关的(scale-invariant)，即独立于测量尺度。

公式如下图：

主要是引入了协方差矩阵，使得特征之间关联起来，对一些单位大小比匹配的特征应该用马氏距离进行计算；

在linear_assignment.py中作为阈值应用，代码如下：

# kf为卡尔曼滤波
gating_distance = kf.gating_distance(
            track.mean, track.covariance, measurements, only_position)	

4、计算代价矩阵

作用：比较feature和targets之间的距离，返回一个代价矩阵；

代码实现在nn_matching.py中：

 def distance(self, features, targets):
     cost_matrix = np.zeros((len(targets), len(features)))
     for i, target in enumerate(targets):
     cost_matrix[i, :] = self._metric(self.samples[target], features)
     return cost_matrix

最终得到的目标对应embedding后特征的代价矩阵，记录当前帧下每个id对应特征；

IOU

上图表示IOU的计算方法，也就是交集比上并集；

首先需要说明numpy.c_的用法，可以合并两个矩阵，代码如下：

>>> np.c_[np.array([1,2,3]), np.array([4,5,6])]
array([[1, 4], 
       [2, 5],
       [3, 6]])

计算两个bounding box的IOU，代码在iou_matching.py中：

def iou(bbox, candidates):
    bbox_tl, bbox_br = bbox[:2], bbox[:2] + bbox[2:]
    candidates_tl = candidates[:, :2]
    candidates_br = candidates[:, :2] + candidates[:, 2:]

    tl = np.c_[np.maximum(bbox_tl[0], candidates_tl[:, 0])[:, np.newaxis],
               np.maximum(bbox_tl[1], candidates_tl[:, 1])[:, np.newaxis]]
    br = np.c_[np.minimum(bbox_br[0], candidates_br[:, 0])[:, np.newaxis],
               np.minimum(bbox_br[1], candidates_br[:, 1])[:, np.newaxis]]
    wh = np.maximum(0., br - tl)

    area_intersection = wh.prod(axis=1)
    area_bbox = bbox[2:].prod()
    area_candidates = candidates[:, 2:].prod(axis=1)
    return area_intersection / (area_bbox + area_candidates - area_intersection)

计算track和detection的成本矩阵，代码在iou_matching.py中：

def iou_cost(tracks, detections, track_indices=None,
             detection_indices=None):
    if track_indices is None:
        track_indices = np.arange(len(tracks))
    if detection_indices is None:
        detection_indices = np.arange(len(detections))

    cost_matrix = np.zeros((len(track_indices), len(detection_indices)))
    for row, track_idx in enumerate(track_indices):
        if tracks[track_idx].time_since_update > 1:
            cost_matrix[row, :] = linear_assignment.INFTY_COST
            continue

        bbox = tracks[track_idx].to_tlwh()
        candidates = np.asarray(
            [detections[i].tlwh for i in detection_indices])
        cost_matrix[row, :] = 1. - iou(bbox, candidates)
    return cost_matrix

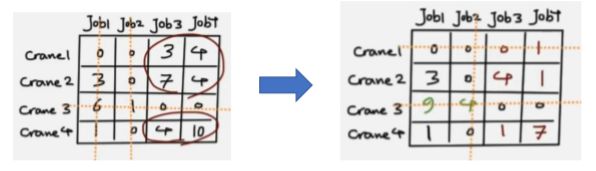
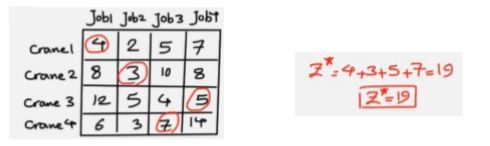
匈牙利算法

定义：是一种在多项式时间内求解任务分配问题的组合优化算法；

作用：可以理解成有N个工人和任务，权重为每个工人对应任务的成本，使得总成本最低；在目标跟踪中用于当前时刻的检测框于上一时刻的检测框得到的跟踪框进行匹配；实质是一个分配指派问题；

实现步骤：

①找到每一行最小值并减去该值；

②找到每一列最小值并减去该值；

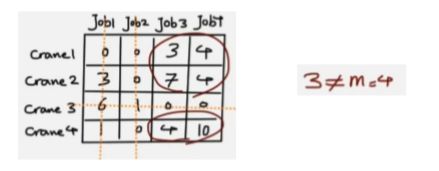
③通过划线将所有0覆盖，覆盖的行列数m是否大于3（大于三则跳出步骤，否则执行④）

④对未覆盖部分取最小值，并且未覆盖的数减去这个值，划线交界处加上这个值，再做一次第三步判断；

⑤在执行一次第四步操作，再执行第三步判断；

最终得到最佳匹配的结果，取每一个工人对应的每一个任务，需要保证四个取值都为0；

最终对应到原始矩阵图中可得到最优的组合；

上述匈牙利算法在跟踪任务中用于计算代价矩阵的最低成本组合；

在linear_assignment.py中对余弦成本矩阵和IOU成本矩阵使用匈牙利算法，代码如下：

from scipy.optimize import linear_sum_assignment

# 传入成本矩阵，得到指派成功的索引对
row_indices, col_indices = linear_sum_assignment(cost_matrix)

卡尔曼滤波

定义：利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计；

实现步骤：

① 初始化参数矩阵

② 测量数据

③ 修正结果

④ 更新参数

由于涉及多个公式及一些数学定义，在此就不作过多的理论讲解，详细可参考以下文章：

博客文章：https://blog.csdn.net/hjxu2016/article/details/114102906

代码中卡尔曼滤波分为两个阶段：

（1）预测track在下一时刻的位置；

（2）基于detection来更新预测的位置；

在kalman_filter.py中实现卡尔曼滤波，代码如下：

# 第一阶段：预测
def predict(self, mean, covariance):
    #卡尔曼滤波器由目标上一时刻的均值和协方差进行预测。
    std_pos = [
        self._std_weight_position * mean[3],
        self._std_weight_position * mean[3],
        1e-2,
        self._std_weight_position * mean[3]]
    std_vel = [
        self._std_weight_velocity * mean[3],
        self._std_weight_velocity * mean[3],
        1e-5,
        self._std_weight_velocity * mean[3]]
       
	# 初始化噪声矩阵Q；np.r_ 按列连接两个矩阵
	# motion_cov是过程噪声 W_k的 协方差矩阵Qk 
	motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))

    # Update time state x' = Fx (1)
    # x为track在t-1时刻的均值，F称为状态转移矩阵，该公式预测t时刻的x'
    # self._motion_mat为F_k是作用在 x_{k-1}上的状态变换模型
    mean = np.dot(self._motion_mat, mean)
    # Calculate error covariance P' = FPF^T+Q (2)
    # P为track在t-1时刻的协方差，Q为系统的噪声矩阵，代表整个系统的可靠程度，一般初始化为很小的值，
    # 该公式预测t时刻的P'
    # covariance为P_{k|k} ，后验估计误差协方差矩阵，度量估计值的精确程度
    covariance = np.linalg.multi_dot((
    self._motion_mat, covariance, self._motion_mat.T)) + motion_cov

	return mean, covariance

# 投影状态分布到测量空间
def project(self, mean, covariance):
	std = [
        self._std_weight_position * mean[3],
        self._std_weight_position * mean[3],
        1e-1,
        self._std_weight_position * mean[3]]
            
	# R为测量过程中噪声的协方差；初始化噪声矩阵R
	innovation_cov = np.diag(np.square(std))

    # 将均值向量映射到检测空间，即 Hx'
    mean = np.dot(self._update_mat, mean)
    # 将协方差矩阵映射到检测空间，即 HP'H^T
    covariance = np.linalg.multi_dot((
    	self._update_mat, covariance, self._update_mat.T))
    return mean, covariance + innovation_cov # 根据公式

# 第二阶段：校正
def update(self, mean, covariance, measurement):
	# 将均值和协方差映射到检测空间，得到 Hx'和S
	projected_mean, projected_cov = self.project(mean, covariance)
	chol_factor, lower = scipy.linalg.cho_factor(
            projected_cov, lower=True, check_finite=False)
    kalman_gain = scipy.linalg.cho_solve(
            (chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
            check_finite=False).T
            
    # H称为测量矩阵，它将track的均值向量x'映射到检测空间，该公式计算detection和track的均值误差
	innovation = measurement - projected_mean
	
	# 更新后的均值向量 x = x' + Ky (6)
	new_mean = mean + np.dot(innovation, kalman_gain.T)
	# 更新后的协方差矩阵 P = (I - KH)P' (7)
	new_covariance = covariance - np.linalg.multi_dot((
            kalman_gain, projected_cov, kalman_gain.T))
	return new_mean, new_covariance

总结

SORT是目标跟踪的关键性算法，为之后的DeepSORT奠定了很好的基础，也是目前主流的目标跟踪算法；本文从如何关联检测网络输出的数据开始讲起，介绍了距离度量、IOU匹配、匈牙利算法和卡尔曼滤波这四种关键方法，这也是SORT的核心部分；关于距离度量以及匈牙利算法比较容易理解，并且代码实现上也并不复杂，而卡尔曼滤波实现相对比较复杂，本文没有过多的介绍，详情可参考我推荐的文章来理解公式并推理；

下一篇将讲解对SORT的拓展，并实现行人和车辆的简单跟踪和计数，对于检测目标而言，无非是检测网络输出的目标不同，跟踪部分的实现基本是不变的；并且SORT有个较大的缺点是容易造成ID Switch，特别是在遮挡的情况下，在之后的DeepSORT中会使用ReID来解决这个问题，减少45%的ID Switch，请持续关注！