详解哈夫曼树和哈夫曼编码

---

哈夫曼树

定义：带权路径长度最短的树

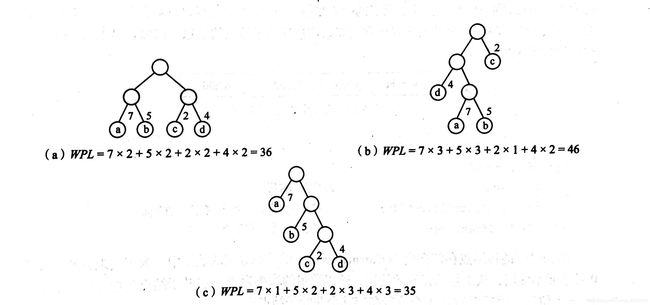
如上图三棵二叉树，都包含4个叶子结点a、b、c、d，分别带权7、5、2、4，它们的带权路径长度分别为36(a),46(b),35c。
显然，c树带权路径长度最小，经验证c树即为哈夫曼树。

哈夫曼树的结构：

typedef struct
{
	int weight;
	int parent,lchird,rchild;
}HTNode,*HuffmanTree;

---

初始化哈夫曼树

说明：初始化带有n个叶子结点的哈夫曼树。

void InitHuffmanTree(HuffmanTree &H,int n)
{
	if(n<=1) return ;
	int m=2*n-1;
	H=new HTNode[m+1];
	for (int i = 1; i <= m; i++)
	{
		H[i].parent=0;
		H[i].lchird=0;
		H[i].rchild=0;
	}
	for (int i = 1; i <= n; i++)
	{
		cin>>H[i].weight;
	}
}

实现：①二叉树的结点数m=2*n-1，n为二叉树的叶子结点数。
②为了实现方便，从数组下标为1的位置开始使用，所以分配m+1个空间。
③将叶子结点存储在前面1~n个位置，后面n-1个位置存储构造后的其他节点。

---

构造哈夫曼树

void CreateHuffmanTree(HuffmanTree &H,int n)
{
	int m=2*n-1;
	int s1,s2;
	for (int i = n+1; i <= m; i++)
	{
		Select(H,i-1,s1,s2);
		H[s1].parent=i; H[s2].parent=i;
		H[i].lchird=s1; H[i].rchild=s2;
		H[i].weight=H[s1].weight+H[s2].weight;
	}
}

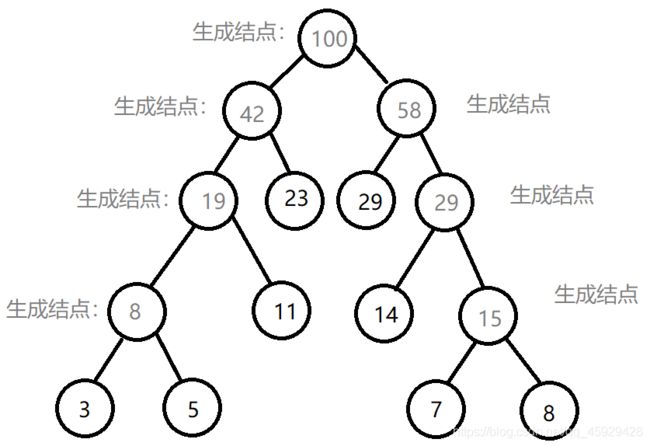
实现：Select()函数的作用为每次选择前1到i-1个结点，挑选两个双亲域为0且权值最小的节点，利用s1和s2返回两个结点的下标。
接着将两个节点的双亲域赋值为当前节点的下标i，将当前节点的孩子域分别置为s1和s2.
最后将两个节点权值相加，和储存在当前“生成”结点的weight。

此哈夫曼树带权路径长度为：23x2+29x2+11x3+14x3+3x4+5x4+7x4+8x4=271

---

Select()

bool cmp(HTNode a,HTNode b)
{
	return a.weight<b.weight;
}
void Select(HuffmanTree H,int l,int &s1,int &s2)
{
	HuffmanTree M;
	M=new HTNode[l+1];
	for (int i = 1; i <= l; i++)
	{
		M[i].weight=H[i].weight;
		M[i].parent=H[i].parent;
		M[i].lchird=H[i].lchird;
		M[i].rchild=H[i].rchild;
	}
	sort(M+1,M+l+1,cmp);
	int a[2]={0};
	int num=0;
	for (int i = 1; i <= l; i++)
	{
		if(M[i].parent==0) 
		{
			for (int j = 1; j <= l; j++)
			{
				if(M[i].weight==H[j].weight&&H[j].parent==0&&j!=a[0])
				{
					a[num++]=j;
					break;
				}
			}
		}
		if(num==2) break;
	}
	s1=a[0];
	s2=a[1];
	delete M;
}

实现：创建一个副本M，每次将待查找的前1-l个单元复制给M，接着对M按照权值由低到高排序。
接着匹配原树和副本，查找权值最小且双亲域为0的两个结点，存储这两个结点本身（在原树中）的下标。
j!=a[0]避免了权值相等时重复添加同一结点的情况。

创建副本的操作目的是不改变原树中结点的位置。
即1-n仍然是叶子结点，n+1~m为创建的节点。

---

哈夫曼编码

哈夫曼编码：对一棵具有n个叶子的哈夫曼树，若对树中的每个左分支赋0，右分支赋1，则从根到每个叶子的路径上，各分支的赋值分别构成一个二进制串，该二进制串就称为哈夫曼编码。
哈夫曼编码的基本思想是：为出现次数较多的字符编以较短的编码，在压缩原理中有重要作用。

如图，各叶子对应哈夫曼编码。
哈夫曼编码表的存储表示：

typedef char** HuffmanCode;

利用二级指针存储每个叶子的哈夫曼编码。

---

根据哈夫曼树求哈夫曼编码

void CreateHuffmanCode(HuffmanTree H,HuffmanCode &HC,int n)
{
	HC=new char*[n+1];
	char* cd=new char[n];
	cd[n-1]='\0';
	for (int i = 1; i <= n; i++)
	{
		int start=n-1;
		int c=i;
		int f=H[i].parent;
		while (f!=0)
		{
			--start;
			if (H[f].lchird==c)
			{
				cd[start]='0';
			}
			else cd[start]='1';
			c=f;
			f=H[f].parent;
		}
		HC[i]=new char[n-start];
		strcpy(HC[i],&cd[start]);
	}
	delete cd; 
}

利用cd存储每个字符的哈夫曼编码，start指向最后一个位置，f指向当前节点的双亲节点，c储存当前节点的下标。
不断向上遍历，若当前节点是双亲的左儿子就赋值0，右儿子就赋值1。
继续更新f和c向上遍历，直到走到树根，f==0（树根双亲域为0）。
接着申请[n-start]空间的内存，将求得的编码从临时空间cd复制到HC的当前行中。

哈夫曼树可以不是唯一的，只要满足和带权路径长度最小值相等的树都是哈夫曼树。显然，哈夫曼编码也不唯一。

---

测试代码

int main()
{
	HuffmanTree H;
	HuffmanCode HC;
	int n;
	cin>>n;
	InitHuffmanTree(H,n);
	CreateHuffmanTree(H,n);
	CreateHuffmanCode(H,HC,n);
	for (int i = 1; i <= n; i++)
	{
		cout<<HC[i]<<endl;
	}
	return 0;
}

运行实例