【LeetCode】set集合+哈希表+快慢指针

LC热评 这就是我的真实想法（呜呜呜
一大清早，两眼睁开，三读题目，四处优化 ，掉了五六七根头发 ，八点开始提交，九遍不过 ，十分伤心 。
十读评论，九看题解，bug不断七窍生烟 ，想了六五四种方法， 三省而后复制，双击鼠标 ，一等舒服。

set集合本身的值是不重复的 ，无序的

349. 两个数组的交集

set的使用

输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的， 同时可以不考虑输出结果的顺序所以可以使用set集合

1.创建set集合存储一个数组的值
2.如果set的值在另一个数组里存在，那就将该值存储在另一个set集合中
3.将set转化为数组即可

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        if(nums1 ==null || nums2 == null || nums2.length == 0 || nums1.length == 0)
        return new int[0];
         Set<Integer>  set1 = new HashSet<>();
         Set<Integer>  set2 = new HashSet<>();
          for( int i : nums1){
              set1.add(i);
          }
          for(int i :nums2){
              if(set1.contains(i)){
                  set2.add(i);
              }
          }
          int[] sum = new int[set2.size()];
          int index= 0;
          for(int i : set2){
              sum[index++] = i;
          }
            return sum;
    }
}

---

350. 两个数组的交集 II

方法一：哈希表

首先遍历第一个数组，并在哈希表中记录第一个数组中的每个数字以及对应出现的次数，然后遍历第二个数组，对于第二个数组中的每个数字，如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。

为了降低空间复杂度，首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数，然后遍历较长的数组得到交集。

map 的key 为nums2的数字，value为nums2数字出现的次数

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        if(nums1.length > nums2.length){
            return intersect(nums2,nums1);
        }
        Map<Integer,Integer> map  = new HashMap<Integer,Integer>();
        for( int i :nums2){
            int  num =map.getOrDefault(i,0);
            map.put(i,num+1); 
        }
        int[] sum = new int[nums1.length];
        int index  =0 ;
        for(int i : nums1){
            int count = map.getOrDefault(i,0);
            if(count > 0){
                count--;
                sum[index++] = i;
                if(count >0){
                    map.put(i,count);
                }else{
                    map.remove(i);
                }

            }
        }
        return Arrays.copyOfRange(sum,0,index);

    }
}

第二种方法：排序 + 双指针

如果果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。

初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        int [] sum = new int[Math.min(nums1.length,nums2.length)];
        int index1 = 0,index2 = 0, index = 0;
        while(index1 <nums1.length && index2 <nums2.length){
            if(nums1[index1] < nums2[index2]){
                index1++;
            }else if(nums1[index1] > nums2[index2]){
                index2++;
            }else{
                index2++;
                sum[index++] = nums1[index1++];    
            }
        }
        return Arrays.copyOfRange(sum,0,index);
    }
}

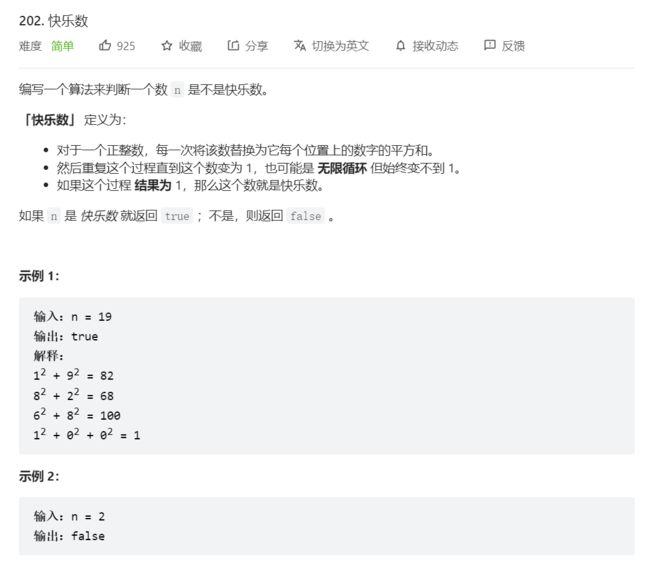
202. 快乐数

哈希表做法

首先判断循环:

1.如果他是快乐数，那他就不会进入循环。

2.当他不是快乐数时，他最终还是会进入循环。

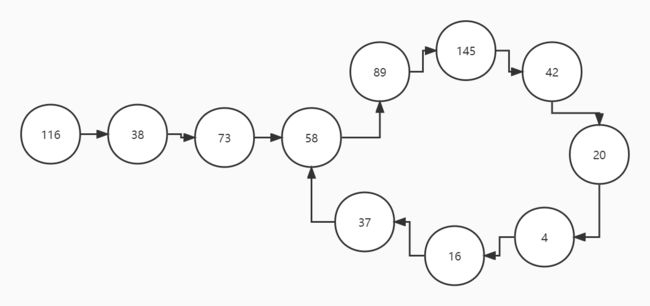
这时，我们还有一个疑问，那本来这个数很大，在循环过程中，他越来越大，最后接近无穷大么？

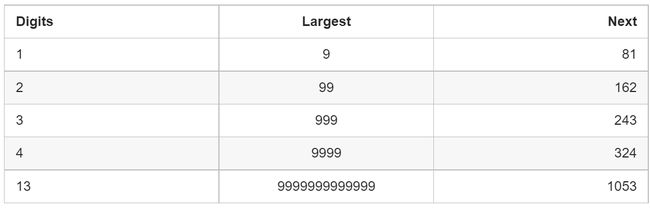
对于 33 位数的数字，它不可能大于 243243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。

意思是说：数在循环过程中会越来越小，会在一个很小的范围内不断循环，不会越来越大，因为每一位的数字的平方就限制了他的大小范围。

算法为：
1.给一个数字 nn，它的下一个数字是什么？
2.按照一系列的数字来判断我们是否进入了一个循环。

第 1 部分我们按照题目的要求做数位分离，求平方和。

第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。

1.如果它不在哈希集合中，我们应该添加它。
2.如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false

class Solution {
    public boolean isHappy(int n) {
        Set<Integer> set = new HashSet<>();
        while(n != 1 && !set.contains(n)){
            set.add(n);
            n = getNextNumber(n);
        }
        return n == 1;
    }

    private int getNextNumber( int n ){
        int res = 0;
        while(n > 0){
            int i = n % 10;
            res += i*i;
            n = n /10;
        }
        return res;
    }
}

方法二：快慢指针

使用 “快慢指针” 思想，找出循环：“快指针” 每次走两步，“慢指针” 每次走一步，当二者相等时，即为一个循环周期。此时，判断是不是因为 1 引起的循环，是的话就是快乐数，否则不是快乐数。

class Solution {
    public boolean isHappy(int n) {
       int fast = n , slow =n;
       do{
           slow = getNextNumber(slow);
           fast = getNextNumber(fast);
           fast = getNextNumber(fast);
       }while(fast != slow);
       return fast ==1;
    }

    private int getNextNumber( int n ){
        int res = 0;
        while(n > 0){
            int i = n % 10;
            res += i*i;
            n = n /10;
        }
        return res;
    }
}