数据结构—栈的应用举例【算术表达式求值转换、后缀表达式求值计算】
- 个人网站: 路遥叶子
- 版权: 本文由【路遥叶子】原创、在CSDN首发、需要转载请联系博主
- 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦
- 想寻找共同成长的小伙伴，请点击【Java全栈开发社区】
目录
栈的应用
带你走进Java后缀表达式的世界！
表达式求值问题：编程实现算术表达式求值。
一、什么是算术表达式？表达式又分为那3种表示形式？
二、请举例说明一下表达式的三种形式？
三、计算表达式的值采用哪种表达形式好呢？
四、求算术表达式值的步骤分那几步？
第一步：将原算术表达式转换成后缀表达式：
五、运算符栈
六、实现转换的基本思路和规则！
七、计算后缀表达式值的算法的基本思路！
第二步：计算后缀表达式的值。
八、程序代码实现后缀表达式计算其值！
1. 链栈类【LinkStack】
2. 后缀表达式，计算值类 【Example3】
3. 测试类【Example3_Text】
4. 测试结果
章节仅是博主阅读书籍的总结和理解，若有不对或欠妥的地方，还请各位大佬批评指正！！！
如果觉得文章对您有帮助，就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来，让我们一起加油学习。博主会不断推出更多优质文章哟
栈的应用
带你走进Java后缀表达式的世界！
表达式求值问题：编程实现算术表达式求值。
一、什么是算术表达式？表达式又分为那3种表示形式？
是由操作数、算术运算符和分隔符所组成的式子。
表达式一般有中缀表达式，后缀表达式和前缀表达式共3种表示形式。
中缀表达式：是将运算符放在两个操作数的中间。日常生活中编写的加减乘除都是中序表达式。
后缀表达式：也称逆波兰表达式，是将运算符放在两个操作数之后。
前缀表达式：是将运算符放在两个操作数之前。
------------------------------------------------------------------------
二、请举例说明一下表达式的三种形式？
例：
中缀表达式：A+(B-C/D) * E
后缀表达式：ABCD/-E*+
前缀表达式：+A *- B/CDE
三、计算表达式的值采用哪种表达形式好呢？
由于运算符又优先级，所以中缀表达式在描述时，对计算非常不方便，特别是待括号的更麻烦。
而后缀表达式中既无运算符的优先级又无括号的约束问题。在后缀表达式中运算符出现的顺序正是计算的顺序。故而使用后缀表达式更好计数。
------------------------------------------------------------------------
四、求算术表达式值的步骤分那几步？
求算术表达式的值可分为两步来进行：
第一步：将原算术表达式换成后缀表达式。
第二步：再对后缀表达式进行求值。
第一步：将原算术表达式转换成后缀表达式：
后缀表达式中的操作数和原算术表达式的先后次序一样，只是运算符的次序不一样；则只需将转换的重点放在运算符的处理上即可。
运算符的优先级表：
注：优先级别从高到低依次用0~3的数字来表示，数字越大，表示其运算符的优先级越高。
------------------------------------------------------------------------
五、运算符栈
使用一个栈来记录保留还未送往后缀表达式的运算符，称为运算符栈。
入栈：新入栈的运算符比栈里的运算符优先级要高。如果是‘（’进行入栈操作。
出栈：新入栈的运算符没有栈里的运算符优先级高，栈里的运算符需要出栈。如果是‘）’出栈直到‘（’
例：已知中序表达式为 8-（3+2*6）/ 5 + 2 ^ 2 ； 求后缀表达式？
解析：
------------------------------------------------------------------------
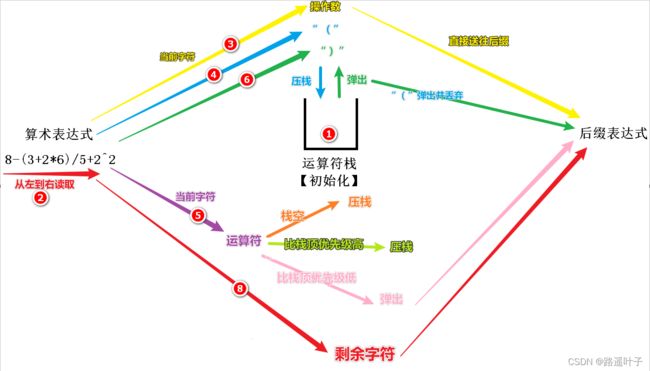
六、实现转换的基本思路和规则！
(1) 初始化一个运算符栈
(2) 从算术表达式输入的字符串，从左到右读取一个字符。
(3) 若当前字符是操作数，则直接送往后缀表达式。
(4) 若当前字符是左括号“ （ ” 时，将其进行压栈到运算符栈
(5) 若当前字符为运算符时,则：
1.当运算符栈空时，进行压栈。
2.当此运算符的优先级高于栈顶运算符时，进行压栈。反之，弹出栈顶运算符送往后缀式，并将当前运算符压栈，重复步骤（5）
(6) 若当前字符为右括号“ ）”时，反复将栈顶符号弹出，并送往后缀表达式，直到栈顶符为左括号“（ ” 为止，在将左括号出栈并丢弃。
(7) 若还未读取完毕，则跳转到(2)
(8) 读取完毕，将栈这剩余的所有运算符弹出并送往后缀表达式。
------------------------------------------------------------------------
七、计算后缀表达式值的算法的基本思路！
第二步：计算后缀表达式的值。
步骤：先找到运算符——》在找前面最后出现的两个操作数——》构成一个最小算术表达式——》 一个栈来保留后缀表达式中还未参与运算的操作数【操作数栈】
基本思路：
(1) 初始化一个操作数栈
(2) 从左到右依次读入后缀表达式中的字符。
1. 若当前字符是操作数，则压栈。
2. 若当前字符是运算符，则从栈顶弹出两个操作数并分别作为第2个操作数和第1个操作数参与运算，在将运算结果进行压栈操作。
(3) 重复步骤(2) 直到读入的后缀表达式结束为止。即操作数栈中的栈顶元素为表达式的计算结果。
------------------------------------------------------------------------
八、程序代码实现后缀表达式计算其值！
1. 链栈类【LinkStack】
package data.linear_table.stack_queue;
import data.linear_table.node.Node;
//链栈类
public class LinkStack implements IStack {
private Node top ; //栈顶元素的引用
//将栈置空
@Override
public void clear() {
top = null ;
}
//判断链栈是否为空
@Override
public boolean isEmpty() {
return top == null ;
}
//求链栈的长度
@Override
public int length() {
Node p = top ; //初始化,p指向栈顶元素
int length = 0 ; //length为计数器
//从栈顶元素开始向后查找，直到p为空
while (p != null ) {
p = p.next ; //p指向后继结点
length++ ; //长度增加1
}
return length ;
}
//取栈顶元素并返回其值
@Override
public Object peek() {
//栈如果不为空
if (!isEmpty()) {
//返回栈顶元素
return top.data ;
}else {
return null ;
}
}
//入栈
@Override
public void push(Object x) throws Exception {
//构造一个新结点
Node p = new Node(x) ;
p.next = top ; //p的指针域指向栈顶元素
top = p ; //新结点成为当前的栈顶元素
}
//出栈
@Override
public Object pop() {
if (isEmpty()) {
return null ;
}else {
Node p = top ; //p指向被删除的结点（栈顶元素）。 用于记录被删除的结点，以便返回删除的值
top = top.next ; //修改链指针，使栈顶结点从链栈中移去
return p.data ; //返回栈顶结点的数据域值
}
}
//输出栈中所有数据元素（从栈顶元素到栈底元素）
public void display() {
Node p = top ; //初始化，p指向栈顶元素
while (p != null ) { //输出所有非空结点的数据元素值
System.out.print(p.data.toString()+" ");
p = p.next ; //p指针向后移
}
}
}
2. 后缀表达式，计算值类 【Example3】
类中方法如下：
1、 将算术表达式转换为后缀表达式的函数，结果以字符串的形式进行返回
package data.linear_table.test;
import data.linear_table.stack_queue.LinkStack;
//将算术表达式转换为后缀表达式的函数，结果以字符串的形式进行返回
//expression 参数为要转换的算术表达式
public String convertToPostFix(String expression) throws Exception {
LinkStack st = new LinkStack(); //初始化一个运算符栈
String postfix = new String(); //用于存放输出的后缀表达式
for (int i = 0; expression != null && i < expression.length(); i++) {
char c = expression.charAt(i); //从算术表达式中读取一个字符
if (c != ' ') { //判断c不为空格
if (isOpenParenthesis(c)) {
//为开括号 '（ ',压栈
st.push(c);
} else if (isCloseParenthesis(c)) {
//为闭括号 ' ) ' ,弹出
char ac = (Character) st.pop(); //强制类型转换，弹出栈顶元素；
while (!isOpenParenthesis(ac)) { //循环一直到ac为开括号 （ 为止
postfix = postfix.concat(String.valueOf(ac)); //串联到后缀表达式的结尾
ac = (Character) st.pop(); //继续弹出元素
}
} else if (isOperator(c)) {
//为运算符时
if (!st.isEmpty()) { //判断栈非空时，取出栈顶优先级高的运算符送往后缀表达式
Character ac = (Character) st.pop();
while (ac!=null && priority(ac.charValue()) >= priority(c)) {
postfix = postfix.concat(String.valueOf(ac)); //串联到后缀表达式的结尾
ac = (Character) st.pop(); //继续弹出
}
if (ac != null) { //若最后一次取出的优先级低的操作符，重新压栈
st.push(ac);
}
}
st.push(c); //压栈
}else {
//为操作数
postfix = postfix.concat(String.valueOf(c)); //串联到后缀表达式的结尾
}
}
}
while (! st.isEmpty()) { //栈中剩余所有的操作符，串联到后缀表达式结尾
postfix = postfix.concat(String.valueOf(st.pop())) ;
}
return postfix ;
}2、判断字符串是否为运算符
//判断字符串是否为运算符
public boolean isOperator(char c) {
//判断c是否等于 +-*/^ %
if ('+' == c || '-' == c || '*' == c || '/' == c || '^' == c || '%' == c) {
return true ;
}else {
return false ;
}
}3、判断字符串是否为开括号 ’ （ ‘
//判断字符串是否为开括号
public boolean isOpenParenthesis (char c) {
return '(' == c ;
}4、判断字符串是否为闭括号’ ）‘
//判断字符串是否为闭括号
public boolean isCloseParenthesis(char c) {
return ')' == c ;
}5、判断运算法的优先级
//判断运算法的优先级
public int priority(char c) {
if (c == '^') { //为幂运算
return 3 ;
}
if (c == '*' || c == '/' || c == '%' ) { //为乘除，取模运算
return 2 ;
}else if (c == '+' || c == '-') { //为加减运算
return 1 ;
}else { //其他运算
return 0 ;
}
}
}
6、对后缀表达式进行求值计算
//对后缀表达式进行求值计算
public double numberCalculate(String postfix) throws Exception {
LinkStack st = new LinkStack(); //初始化一个操作数栈
for (int i = 0 ; postfix != null && i < postfix.length(); i++ ) {
char c = postfix.charAt(i); //从后缀表达式中读取第一个字符
//当c为操作符时
if (isOperator(c)) {
//取出两个操作数
//st.pop出栈，将前面的两个元素取出
double d2 = Double.valueOf(st.pop().toString());
double d1 = Double.valueOf(st.pop().toString());
double d3 = 0 ;
if ('+' == c) { //加法运算
d3 = d1 + d2 ;
}else if ('-' == c) { //减法运算
d3 = d1 -d2 ;
}else if ('*' == c ) { //乘法运算
d3 = d1 * d2 ;
}else if ('/' == c ) { //除法运算
d3 = d1 / d2 ;
}else if ('^' == c ) { //幂运算
d3 = Math.pow(d1,d2);
}else if ('%' == c ) { //取模
d3 = d1 % d2 ;
}
//将处理结果，压栈到操作数栈
st.push(d3);
}else {
//为操作数时，直接压栈
st.push(c);
}
}
//返回运算结果，栈顶出栈
return (Double) st.pop();
} 3. 测试类【Example3_Text】
package data.linear_table.test;
public class Example3_Text {
public static void main(String[] args) throws Exception {
//创建后缀表达式，计算值类
Example3 p = new Example3();
//调用方法转换为后缀表达式
String postfix = p.convertToPostFix("(1+2)*(5-2)/2^2+5%3");
System.out.println("转换的后缀表达式为："+postfix);
//对后缀表达式求值，并输出
System.out.println("计算后缀表达式的结果为：" + p.numberCalculate(postfix));
}
}
4. 测试结果
----------------------------------------------------------------------------
章节仅是博主阅读书籍的总结和理解，若有不对或欠妥的地方，还请各位大佬批评指正！！！
如果觉得文章对您有帮助，就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来，让我们一起加油学习。博主会不断推出更多优质文章哟
想要了解更多吗？没时间解释了，快来点一点！
《数据结构-Java语言描述》打卡第一天
https://blog.csdn.net/zsy3757486/article/details/123735691?spm=1001.2014.3001.5501 《数据结构-Java语言描述》打卡第二天https://blog.csdn.net/zsy3757486/article/details/123786120?spm=1001.2014.3001.5501《数据结构-Java语言描述》打卡第三天https://blog.csdn.net/zsy3757486/article/details/123810848?spm=1001.2014.3001.5501 《数据结构-Java语言描述》打卡第四天https://blog.csdn.net/zsy3757486/article/details/123846758?spm=1001.2014.3001.5501《数据结构-Java语言描述》打卡第五天https://blog.csdn.net/zsy3757486/article/details/123862163?spm=1001.2014.3001.5501《数据结构-Java语言描述》打卡第六天https://blog.csdn.net/zsy3757486/article/details/123894111?spm=1001.2014.3001.5501