动态规划算法思想和应用

一. 动态规划算法

1. 动态规划算法思想

算法的基本思想与分治算法类似，也是将待求问题划分为若干个子问题，按划分的顺序求解子阶段问题，前一个子问题的解，为后一个子问题的求解提供了有用的信息（最优子结构）。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其它局部解。依次解决各个子问题，最后求出原问题的最优解。

与分治算法最大的区别：适合于用动态规划算法求解的问题，经分解后得到的子问题往往不是相互独立的。

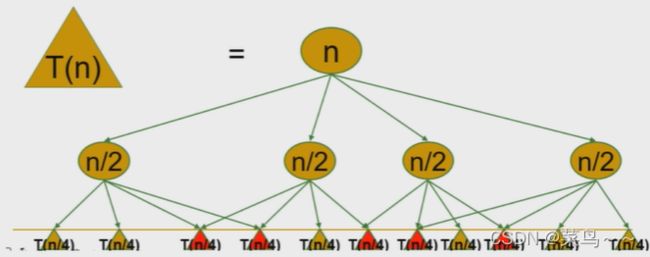
什么问题能用动态规划解决？用动态规划解决需要考虑哪些东西？

2. 动态规划求解问题的基本步骤

动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过中间阶段决策的选择，达到结束状态。动态规划算法的代码设计都有一定的模式，一般经过以下几个步骤：

初始状态->决策1->决策2->…->决策n->结束状态

1. 找出最优解的性质，并刻画其结构特征（找问题状态）
2. 递归地定义最优值（找状态转移方程）
3. 自底向上的方式计算最优值
4. 根据计算最优值时得到的信息，构造最优解

二. 动态规划算法问题案例

1. 硬币选择问题

有1，3，5分面额的硬币，给定一个面值11，问组成的给定面值所需要的最少的硬币数量是多少？

#include
#include
using namespace std;

const int n = 11;

int func1(int n)
{
	if (n == 1 || n == 3 || n == 5)
	{
		return 1;
	}
	if (n == 2 || n == 4)
	{
		return 2;
	}
	else
	{
		int n1 = func1(n - 1) + 1;//选择了1分硬币
		int n2 = func1(n - 3) + 1;//选择了3分硬币
		int n3 = func1(n - 5) + 1;//选择了5分硬币
		return std::min((std::min(n1,n2)),n3);
	}
}
int main()
{
	cout << "最少的硬币数量是：" << func1(n) << endl;
}

用分治法的话，子问题会被重复求解，下面用动态规划解决

递归方法：

#include
#include
using namespace std;

const int n = 100;
int dp[n + 1] = { 0 };//组成价值n需要的硬币最小数量
int cnt = 0;//代码测试

int func1(int n)
{
	if (dp[n] > 0)//dp[n]这个子问题已经被求解过了
	{
		cnt++;
		return dp[n];
	}
	if (n == 1 || n == 3 || n == 5)
	{
		dp[n] = 1;//代表了一个子问题最优解的性质（状态）
		return 1;
	}
	if (n == 2 || n == 4)
	{
		dp[n] = 2;
		return 2;
	}
	else
	{
		int n1 = func1(n - 1) + 1;//选择了1分硬币
		int n2 = func1(n - 3) + 1;//选择了3分硬币
		int n3 = func1(n - 5) + 1;//选择了5分硬币
		dp[n] = std::min((std::min(n1,n2)),n3);
		return dp[n];
	}
}
int main()
{
	cout << "最少的硬币数量是：" << func1(n) << endl;
	cout << cnt << endl;
}

利用状态转移方程

#include
using namespace std;

const int c = 100;
void main()
{
	int v[] = { 1,3,5 };
	int length = sizeof(v) / sizeof(v[0]);
	int* dp = new int[c + 1]();
	for (int i = 1; i <= c; i++)
	{
		dp[i] = i;//表示初始全部由一分硬币组成
		for (int j = 0; j < length; j++)
		{
			if (i >= v[j] && dp[i] > (1 + dp[i - v[j]]))
			{
				dp[i] = 1 + dp[i - v[j]];
			}
		}
	}
	cout << dp[c] << endl;
}

2. 斐波那契数列

常规递归解法：

#include
using namespace std;

int fabnacci(int n)
{
	if (n == 1 || n == 2)
	{
		return 1;
	}
	else
	{
		return fabnacci(n - 1) + fabnacci(n - 2);
	}
}
int main()
{
	int n = 5;
	cout << fabnacci(n) << endl;
	return 0;
}

递归用动态规划实现

#include
using namespace std;

int fabnacci(int n,int dp[])
{
	if (dp[n] > 0)
	{
		return dp[n];
	}
	if (n == 1 || n == 2)
	{
		dp[n] = 1;
		return 1;
	}
	else
	{
		dp[n] = fabnacci(n - 1, dp) + fabnacci(n - 2, dp);
		return dp[n];
	}
}
int main()
{
	int n = 5;
	int* dp = new int[n + 1]();
	cout << fabnacci(n,dp) << endl;
	return 0;
}

转移方程实现

#include
using namespace std;

int main()
{
	const int n = 10;
	int dp[n + 1] = { 0 };
	dp[1] = dp[2] = 1;
	for (int i = 3; i <= n; i++)
	{
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	cout << dp[n] << endl;
	return 0;
}

3. 最大子段和问题

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的字段和的最大值。当所给的整数均为负数时定义字段和为0，如果序列中全部是负数则最大字段和为0，依此定义，所求的最优值为Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。

#include
using namespace std;

int main()
{
	int arr[] = { -2,11,-4,13,-5,-2 };
	const int n = sizeof(arr) / sizeof(arr[0]);
	int dp[n] = { 0 };//状态
	dp[0] = arr[0] < 0 ? 0 : arr[0];
	int maxval = dp[0];
	for (int i = 1; i < n; i++)
	{
		dp[i] = arr[i] + dp[i - 1];//状态转移方程
		if (dp[i] < 0)
		{
			dp[i] = 0;
		}
		if (dp[i] > maxval)
		{
			maxval = dp[i];
		}
	}
	cout << maxval << endl;
}

4. 最长非降子序列LIS问题

求序列的最长非降子序列长度
分析：

代码实现

#include
using namespace std;

int main()
{
	int arr[] = { 5,3,4,1,8,7,9 };
	const int length = sizeof(arr) / sizeof(arr[0]);
	int dp[length] = { 0 };
	int maxlength = 0;
	for (int i = 0; i < length; i++)
	{
		dp[i] = 1;
		for (int j = 0; j < i; j++)
		{
			if (dp[j] + 1 > dp[i] && arr[j] < arr[i])
			{
				dp[i] = dp[j] + 1;
			}
		}
		if (maxlength < dp[i])
		{
			maxlength = dp[i];
		}
	}
	cout << maxlength << endl;
	return 0;
}

5. LCS最长公共子序列

求两个序列的最长公共子序列的长度

分析：用分治算法

代码实现

#include
#include
#include
using namespace std;

string s1 = "helloworld";
string s2 = "hlweord";
int n = s1.length();
int m = s2.length();
int cnt = 0;

int LCS(string s1, int n, string s2, int m)
{
	if (n < 0 || m < 0)
	{
		return 0;
	}
	cnt++;
	if (s1[n] == s2[m])
	{
		return LCS(s1, n - 1, s2, m - 1) + 1;
	}
	else
	{
		int l1 = LCS(s1, n - 1, s2, m);
		int l2 = LCS(s1, n, s2, m - 1);
		return max(l1, l2);
	}
}

int main()
{
	cout << "最长子序列长度为：" << LCS(s1, n - 1, s2, m - 1) << endl;
	cout << "cnt:" << cnt << endl;
}

分析分治法：

子问题的划分产生重叠，所以可以用动态规划算法来求解

代码实现

#include
#include
#include
using namespace std;

string s1 = "helloworld";
string s2 = "hlweord";
int n = s1.length();
int m = s2.length();
int cnt = 0;
vector<vector<int>> dp(n, vector<int>(m, -1));

int LCS(string s1, int n, string s2, int m)
{
	if (n < 0 || m < 0)
	{
		return 0;
	}
	if (dp[n][m] >= 0)
	{
		return dp[n][m];
	}
	cnt++;
	if (s1[n] == s2[m])
	{
		dp[n][m] = LCS(s1, n - 1, s2, m - 1) + 1;
	}
	else
	{
		int l1 = LCS(s1, n - 1, s2, m);
		int l2 = LCS(s1, n, s2, m - 1);
		dp[n][m] = max(l1, l2);
	}
	return dp[n][m];
}

int main()
{
	cout << "最长子序列长度为：" << LCS(s1, n - 1, s2, m - 1) << endl;
	cout << "cnt:" << cnt << endl;
}

输出最长公共子序列包括的所有字符
分析：

#include
#include
#include
using namespace std;

string s1 = "helloworld";
string s2 = "hlweord";
int n = s1.length();
int m = s2.length();
int cnt = 0;//代码测试
vector<vector<int>> dp(n, vector<int>(m, -1));
vector<vector<int>> path(n, vector<int>(m, 0));//记录最长子序列

int LCS(string s1, int n, string s2, int m)
{
	if (n < 0 || m < 0)
	{
		return 0;
	}
	if (dp[n][m] >= 0)
	{
		return dp[n][m];
	}
	cnt++;
	if (s1[n] == s2[m])
	{
		dp[n][m] = LCS(s1, n - 1, s2, m - 1) + 1;
		path[n][m] = 1;//向左上方递归
	}
	else
	{
		int l1 = LCS(s1, n - 1, s2, m);
		int l2 = LCS(s1, n, s2, m - 1);
		if (l1 > l2)
		{
			dp[n][m] = l1;
			path[n][m] = 3;//向上方递归
		}
		else
		{
			dp[n][m] = l2;
			path[n][m] = 2;//向左边递归
		}
	}
	return dp[n][m];
}
void backStrace(string s1, int n, int m)
{
	if (n < 0 || m < 0)
	{
		return;
	}
	if (path[n][m] == 1)
	{
		backStrace(s1, n - 1, m - 1);//对角线递归
		cout << s1[n];
	}
	else if (path[n][m] == 2)
	{
		backStrace(s1, n, m - 1);//左递归
	}
	else
	{
		backStrace(s1, n - 1, m);//上递归
	}
}
int main()
{
	cout << "最长子序列长度为：" << LCS(s1, n - 1, s2, m - 1) << endl;
	cout << "cnt:" << cnt << endl;
	backStrace(s1, n - 1, m - 1);
}

LCS非递归实现

#include
#include
#include
using namespace std;

string s1 = "helloworld";
string s2 = "hlweord";
int n = s1.length();
int m = s2.length();

vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
vector<vector<int>> path(n+1, vector<int>(m+1, 0));//记录最长子序列

int LCS(string s1, int i, string s2, int j)
{
	for (int n = 1; n <= i; n++)
	{
		for (int m = 1; m <= j; m++)
		{
			if (s1[n-1] == s2[m-1])
			{
				dp[n][m] = 1 + dp[n - 1][m - 1];
				path[n][m] = 1;
			}
			else
			{
				int l1 = dp[n - 1][m];
				int l2 = dp[n][m - 1];
				if (l1 > l2)
				{
					dp[n][m] = dp[n - 1][m];
					path[n][m] = 3;
				}
				else
				{
					dp[n][m] = dp[n][m - 1];
					path[n][m] = 2;
				}
			}
		}
	}
	return dp[i][j];
}
void backStrace(string s1, int n, int m)
{
	if (n <= 0 || m <= 0)
	{
		return;
	}
	if (path[n][m] == 1)
	{
		backStrace(s1, n - 1, m - 1);//对角线递归
		cout << s1[n-1];
	}
	else if (path[n][m] == 2)
	{
		backStrace(s1, n, m - 1);//左递归
	}
	else
	{
		backStrace(s1, n - 1, m);//上递归
	}
}
int main()
{
	cout << "最长子序列长度为：" << LCS(s1, n , s2, m) << endl;
	cout << "cnt:" << cnt << endl;
	backStrace(s1, n , m);
}

6. 0-1背包问题

分析：

#include
#include
using namespace std;

int main()
{
	int w[] = { 8,6,4,2,5 };
	int v[] = { 6,4,7,8,6 };
	int c = 12;
	int n = sizeof(w) / sizeof(w[0]) - 1;
	vector<vector<int>> dp(n + 1, vector<int>(c + 1, 0));
	//填写初始状态的值
	for (int j = 1; j <= c; j++)
	{
		if (w[n] > j)//第n个物品的重量>背包剩余容量
		{
			dp[n][j] = 0;
		}
		else
		{
			dp[n][j] = v[n];//第n个物品的重量<=背包剩余容量
		}
	}
	//从n-1到0开始表示所选的物品是i,i+1...n
	for (int i = n - 1; i >= 0; i--)
	{
		for (int j = 1; j <= c; j++)
		{
			if (w[i] > j)
			{
				dp[i][j] = dp[i + 1][j];
			}
			else
			{
				dp[i][j] = max(dp[i + 1][j], v[i] + dp[i + 1][j - w[i]]);
			}
		}
	}
	//便于理解问题，打印dp数组
	for (int i = 0; i <= n; i++)
	{
		for (int j = 1; j <= c; j++)
		{
			cout << dp[i][j] << " ";
		}
		cout << endl;
	}
	int bestv = 0;
	cout << "选择的物品价值是：";
	for (int i = 0; i < n; i++)
	{
		if (dp[i][c] != dp[i + 1][c])
		{
			cout << w[i] << " ";
			bestv += v[i];
			c -= w[i];
		}
	}
	if (dp[n][c] > 0)
	{
		cout << w[n] << endl;
	}
	return 0;
}

7. 三角数组求和

给定一个三角形，找出自顶向下的最小路径和，每一步只能移动到下一行中相邻的节点上。

#include
#include
using namespace std;

int main()
{
	vector<int> v1 = { 2 };
	vector<int> v2 = { 3,4 };
	vector<int> v3 = { 6,5,7 };
	vector<int> v4 = { 4,1,8,3 };
	vector<vector<int>> v = { v1,v2,v3,v4 };
	//状态dp[i][j]:第i行第j列开始选择数字的和的最小值
	vector<vector<int>> dp(v.size(), vector<int>(v4.size(),0));

	int n = v.size() - 1;
	for (int i = 0; i < v4.size(); i++)
	{
		dp[n][i] = v[n][i];
	}
	for (int i = n - 1; i >= 0; i--)
	{
		for (int j = 0; j < v[i].size(); j++)
		{
			dp[i][j] = v[i][j] + min(dp[i + 1][j], dp[i + 1][j + 1]);
		}
	}
	cout << dp[0][0] << endl;
}