二叉树练习题分享
**
二叉树是常见的数据结构,本期分享二叉树的升级版算法。难懂的地方本人已经做出注释以及相应的图示分析帮助大家理解。**
文章目录
- 1. 将二叉树的节点转换成括号表达式
-
- (1)做法一:
- (2)做法二:减少拷贝次数,string 的构造次数。
- 2.“新”层序遍历,实现一次出多个,返回一个二维数组。
- 3.二叉树两个节点的最近公共祖先
- 4.二叉树转换为双向链表
- 5.前中序实现二叉树重建
- 6.非递归实现前中后序遍历
-
- 1.非递归实现前序遍历
- 2.非递归实现中序遍历
- 3.非递归实现后序遍历
- 7. 每日分享!
1. 将二叉树的节点转换成括号表达式
(1)做法一:
思路:
- 在字符串中添加字符之前,先加上一个(,递归得到左孩子节点的值的字符后,在加上一个).同理右子树。
- 添加字符时,如果是空节点就直接返回,这时字符串添加的就是空字符,但是注意空字符左右都包含着()。
- 如何去掉这些空括号?
当左子树为空,并且右子树也为空时就不需要添加括号了,因为也没有值让你括。
如果右子树不为空,但是左子树为空,就需要在前面加上一个左子树的空括号,表示。
当左子树不为空,右子树为空时,就不需要添加右子树的空()了。 - 注意||的处理方式,如果左边条件满足了,就不在判断右边的情况了。
代码以及注释理解如下:
string tree2str(TreeNode* root)
{
string str;
if(root==nullptr)
return str;
str += to_string(root->val);
if(root->left || root->right)
//如果左不为空或者左为空右不为空,都需要有()在中间
{
str+='(';
str+= tree2str(root->left);
str+=')';
}
//能下来就说明可能是是左不为空,然后来判断右子树是不是空。
//如果不是空,就正常添加。
//如果是空,就不需要进行处理了。
if(root->right)
{
str+='(';
str+=tree2str(root->right);
str+=')';
}
return str;
}
(2)做法二:减少拷贝次数,string 的构造次数。
用子函数,然后字符串后缀添加时用字符串的引用就可以减少拷贝次数。
string _tree2str(TreeNode* root,string & str)
{
if(root==nullptr)
return str;
str+=to_string(root->val);
if(root->left||root->right)
{
str+='(';
_tree2str(root->left,str);
str+=')';
}
if(root->right)
{
str+='(';
_tree2str(root->right,str);
srt+=')';
}
return str;
}
string tree2str(TreeNode* root)
{
string str;
_tree2str(root,str);
return str;
}
2.“新”层序遍历,实现一次出多个,返回一个二维数组。
每一层一次性放到一个数组当中。
vector<vector<int>> levelorder(TreeNode* root)
{
queue<TreeNode*>q;
int levelsize=0;
if(root)
{
q.push(root);
levelsize=1;
}
vector<vector<int>>vv;
while(!q.empty())
{
//通过levelsize控制一层一层出
vector<int >v;
while(levelsize--)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
//一层出完了,更新到下一层的数据。因为此时队列中都是下一层的数据
levelsize = q.size();
vv.push_back(v);
}
return vv;
}
3.二叉树两个节点的最近公共祖先
注:(自己可以认为是自己的祖先)
- 沿着自己到根节点的路径,两条路径的交点就是最近的祖先
- 如果是搜索树,
a. 一个在我的左树,一个在我的右树,那么我就是公共祖先。
b. 如果都比我小就去左树递归查找; - 普通树
不会用大小去判断是在左右,而是去进行查找Find()函数
如果其中一个就是根节点,就不用找了。
bool Find(TreeNode* root,TreeNode* x)
{
if(root == nullptr)
return false;
if(root == x)
return true;
return Find(root->left , x)||Find(root->right , x);
}
TreeNode* lowestCommonAncestor(TreeNode* root,TreeNode*p,TreeNode* q)
{
if(root==nullptr)
return nullptr;
if(root==p||root==q)//如果自己就是根节点直接返回
return root;
bool pInleft,pInright,qInleft,qInright;//为了确认在左子树还是右子树
pInleft=Find(root->left,p);
pInright=!pInleft;
qInleft=Find(root->left,q);
qInright=!qInleft;
if((pInleft && qInright)||(pInright && qInleft))
return root;
else if(pInleft && qInleft)
return lowestCommonAncestor(root->left,p,q);
else if(pInright && qInright)
return lowestCommonAncestor(root->right,p,q);
else
return nullptr;
}
上述这种算法就是查了太多遍。还有就是很多单边子树,极端为O(N*N)。所以升级算法在下:
bool Findpath(TreeNode* root,TreeNode* x,stack<TreeNode*>&path)
{
if(root==nullptr)
return false;
path.push(root);//先入栈避免节点丢失,先进来再判断
if(root == x)
return true;
//分别去左右子树查找
if(Findpath(root->left,x,path))
return true;
if(Findpath(root->right,x,path))
return true;
//如果这个节点左右都不在,就说明该节点不是路径上的一点,就需要出栈。
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root,TreeNode*p,TreeNode* q)
{
stack<TreeNode*>pPath,qPath;
Findpath(root,p,pPath);
Findpath(root,q,qPath);
//让长的路径先走差距步
while(pPath.size()!=qPath.size())
{
if(pPath.size()>qPath.size())
pPath.pop();
else
qPath.pop();
}
//路径栈顶元素如果相等此时就是最近的共同祖先
while(pPath.top()!= qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
4.二叉树转换为双向链表
二叉搜索树转化为排序的双向链表(二叉树的线索化)和中序遍历有关系
要求不创建任何新的节点,只能调整树中节点指针的指向,左指针充当前驱
右指针当成next。

思路演示:

void InOrder(TreeNode* cur,TreeNode* &prev)
{
if(cur==NUll)
return ;
InOrder(root->left,prev);
cur->left=prev;
if(prev)
prev->right=cur;
prev=cur;
InOrder(root->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
if(pRootOfTree==nullptr)
return nullptr;
TreeNode* prev=nullptr;
InOrder(pRootOfTree,prev);
//找到最左节点进行返回
TreeNode* head=pRootOfTree;
while(head->left)
{
head=head->left;
}
return head;
}
5.前中序实现二叉树重建
通过前序和中序重建二叉树(没有重复数据的前提下)
通过前序确定根的位置,在中序区间,分割左右子树。
注:如果是后序和中序就需要调整一下顺序,posti–,先构建右子树,再构建左子树。
TreeNode* _buildTree(vector<int>& preorder,vector<int>&inorder,int &prei,int inbegin,int inend)
{
if(inbegin>inend)
return nullptr;
TreeNode* root=new TreeNode(preorder[prei]);//实现重构节点
//将中序区分出来
int rooti=inbegin;
while(rooti<=inend)//找到根节点在中序的位置实现分割
{
if(inorder[rooti]==preorder[prei])
break;
else
++rooti;
}
++prei;
//中序被分为[ibegin,rooti-1]rooti[rooti+1,inend]
//重建左子树和右子树
root->left=_buildTree(preorder,inorder,prei,inbegin,inorder.size()-1);
root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
}
TreeNode* buildTree(vector<int>& preorder,vector<int>& inorder)
{
int prei=0;
return _buildTree(preorder,inorder,prei,0,inorder.size()-1);
}
6.非递归实现前中后序遍历
1.非递归实现前序遍历
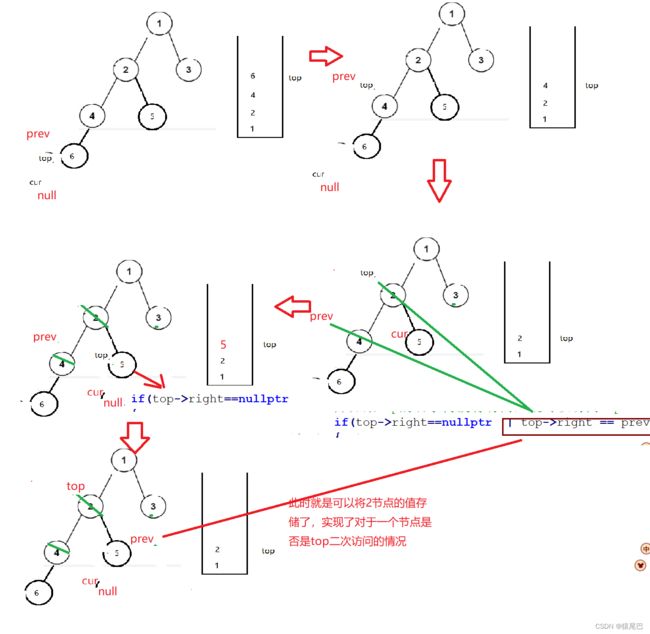
最左侧节点入栈,然后以图示方式访问右子树并将右子树节点值存储。
vector<int>preorderTraveler(TreeNode* root)
{
vector<int>v;
stack<TreeNode*>st;
TreeNode* cur=root;
while(cur||!st.empty())//还没到最左节点||栈中的左节点还没有遍历完
{
//1.访问左路节点,左路节点入栈
while(cur)
{
st.push(cur);
v.push_back(cur->val);
cur=cur->left;
}
//2. 栈里面的左路节点中的左子树没有访问
TreeNode* top=st.top();
st.pop();
//子问题的形式访问右子树
cur=top->right;
}
return v;
}
2.非递归实现中序遍历
中序遍历的思想和前序遍历类似,只是节点的弹出顺序数据存储顺序发生变化,先找到最左节点然后数据存储,不敢先弹出。可结合图示进行理解。
vector<int>inorderTraveler(TreeNode* root)
{
vector<int>v;
stack<TreeNode*>st;
TreeNode* cur=root;
while(cur||!st.empty())
{
//1. 将左子树节点全部入栈
while(cur)
{
st.push(cur);
cur=cur->left;
}
TreeNode* top=st.top();
st.pop();
v.push_back(top->val);
//再去用子问题访问他的右子树
cur=top->right;
}
return v;
}
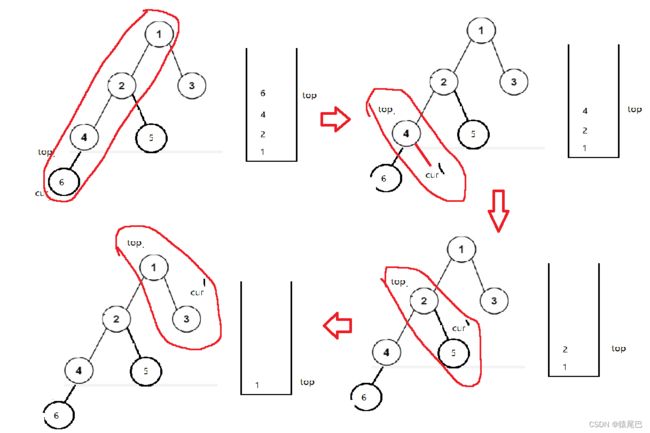
3.非递归实现后序遍历
后序遍历:
由于不能先将节点的值进行访问,当遍历完右子树再访问根节点的值
进行push时就会可能产生是否已经被push的疑问。
那么我们就用一个prev。
如果a右子树节点被访问了,它的前面一定是他的右子树节点。
如果a的前面不是右子树节点,说明他的右子树节点还没有被访问,就需要先访问他的右子树节点。
vector<int>postorderTraveler(TreeNode* root)
{
vector<int>v;
TreeNode*prev=nullptr;
stack<TreeNode*>st;
TreeNode* cur=root;
while(cur||!st.empty())
{
//1. 将左子树节点全部入栈
while(cur)
{
st.push(cur);
cur=cur->left;
}
TreeNode*top=st.top();
//如果右子树已经访问过了,就可以直接访问top
//右子树为空或者上一个访问节点是top右孩子节点,那么表示右子树访问过了,就可以访问top了
//如果top的右子树没有访问,就可以访问top->right
if(top->right==nullptr || top->right == prev)
{
v.push_back(top->val);
prev=top;
st.pop();
}
else
cur=top->right;
}
return v;
}
7. 每日分享!
有的时候,我们会感到无所事事,用很多看似无聊的方式,抱着好奇的想法去尝试一些自认为可以愉悦自己来打发时间的方式,去给自己腾出时间等待学习状态的回暖。这种思想和行为不仅不会有所帮助,很可能会将我们的状态拖得越来越差。可能一两局游戏过后,精神状态会变得更差,这时希望我们能停下来闭上眼睛休息一下,这种方式会起到最好的效果。
希望大家不忘心中理想,继续坚持走下去!!
Carry on!