超参数优化之贝叶斯优化(Bayesian Optimization)
文章目录
-
- Ⅰ.Grid Search/Random Search
- Ⅱ.Bayesian Optimization
Ⅰ.Grid Search/Random Search
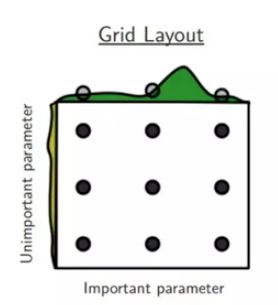
Grid Search:神经网络训练由许多超参数决定,例如网络深度、学习率、卷积核大小等等。为了找到一个最好的超参数组合,最直观的想法就是Grid Search, 其实也就是穷举搜索。
Random Search:为了提高搜索效率,提出随机搜索。虽然随机搜索得到的结果互相之间差异较大,但是实验证明随机搜索的确比网格搜索效果要好
Ⅱ.Bayesian Optimization
贝叶斯优化的大体思路:
假设一组超参数组合是 X = x 1 , x 2 , . . . , x n X = x_1,x_2, ...,x_n X=x1,x2,...,xn, 贝叶斯优化假设超参数与需要优化的损失函数存在一个函数关系。
假设函数 f : x → R , 我 们 需 要 在 x ⊂ X 内 找 到 \ f :x → R, 我们需要在 x \subset X内找到 f:x→R,我们需要在x⊂X内找到
x ∗ = a r g m i n x ∈ X f ( x ) ( 1 ) x^* =\mathop{argmin}\limits_{x \in X}f(x) \qquad (1) x∗=x∈Xargminf(x)(1)
详细算法:
Sequential model-based optimization(SMBO)
I n p u t : f , X , S , M \ {Input: f, X, S, M} Input:f,X,S,M
D ← I n i t S a m p l e s ( f , X ) D \leftarrow InitSamples(f, X) D←InitSamples(f,X)
f o r i ← ∣ D ∣ t o T d o : for \quad i \leftarrow |D| \quad to\quad T \quad do : fori←∣D∣toTdo:
p ( y ∣ x , D ) ← F i t M o d e l ( M , D ) \qquad p(y|x, D) \leftarrow FitModel(M,D) p(y∣x,D)←FitModel(M,D)
x i ← a r g m a x x ∈ X S ( x , p ( y ∣ x , D ) ) \qquad x_i \leftarrow \mathop{argmax}\limits_{x \in X}S(x, p(y|x, D)) xi←x∈XargmaxS(x,p(y∣x,D))
y i ← f ( x i ) ▹ E x p e n s i v e s t e p \qquad y_i \leftarrow f(x_i) \quad \triangleright Expensive \ step yi←f(xi)▹Expensive step
D ← D ∪ ( x i , y i ) \qquad D \leftarrow D\cup (x_i,y_i) D←D∪(xi,yi)
e n d f o r end \ for end for
<1>.Input:
f f f: 就是所谓的黑盒子,即输入一组超参数;得到一个输出值。
X X X: 超参数搜索空间。
D D D: 表示一个由若干对数据组成的数据集,每一对数组表示为 ( x , y ) , x (x,y),x (x,y),x是一组超参数, y y y表示该组超参数对应的结果。
S S S:是Acquisition Function(采集函数) ,这个函数的作用是用来选择 x x x
M M M: 是对数据集D进行拟合得到的模型,可以用来假设的模型有很多种,例如随机森林,Tree Parzen Estimators, 高斯模型。
<2>. D ← I n i t S a m p l e s ( f , X ) D \leftarrow InitSamples(f,X) D←InitSamples(f,X)
这一步骤就是初始化获取数据集 D = ( x 1 , y 1 ) , . . . , ( x n , y n ) , D = (x_1, y_1), ..., (x_n, y_n), D=(x1,y1),...,(xn,yn),其中 y i = f ( x i ) y_i = f(x_i) yi=f(xi)。
<3>.循环选参数T次
因为每次选出参数 x x x后都需要计算 f ( x ) f(x) f(x), 消耗大量资源,所以一般需要固定选参次数(或者是函数评估次数)。
p ( y ∣ x , D ) ← F i t M o d e l ( M , D ) p(y|x,D) \leftarrow FitModel(M, D) p(y∣x,D)←FitModel(M,D)
首先我们预先假设了模型 M M M服从高斯分布, 且已知了数据集 D D D, 所以可以通过计算得出模型的具体函数表示。
高斯分布如何计算?
假设模型 f ∼ G P ( μ , K ) ( G P : 高 斯 过 程 , μ : 均 值 , K : 协 方 差 k e r n e l ) f \sim GP(\mu, K) \quad (GP:高斯过程, \mu: 均值, K:协方差kernel) f∼GP(μ,K)(GP:高斯过程,μ:均值,K:协方差kernel), 所以预测也是服从正态分布的,即 p ( y ∣ x , D ) = N ( y ∣ μ ^ , σ ^ 2 ) p(y|x, D) = N(y|\hat{\mu}, \hat{\sigma}^{2}) p(y∣x,D)=N(y∣μ^,σ^2)
y = ( y i . . . y i ) T \mathbf{y} = (y_i ... y_i)^{T} y=(yi...yi)T
μ ^ = k ( x ) T ( K + σ n 2 I ) − 1 y \hat{\mu} = \mathbf{k(x)}^{T}(\mathbf{K} + \sigma_n^{2}\mathbf{I})^{-1}\mathbf{y} μ^=k(x)T(K+σn2I)−1y
σ ^ 2 = K ( x 1 x ) − k ( x ) T ( K + σ n 2 I ) − 1 k ( x ) \hat{\sigma}^{2} = \mathbf{K}(x_1x) - \mathbf{k}(x)^{T}(\mathbf{K} + \sigma_n^{2}\mathbf{I})^{-1}\mathbf{k}(\mathbf{x}) σ^2=K(x1x)−k(x)T(K+σn2I)−1k(x)
<4>. x i ← a r g m a x x ∈ X S ( x , p ( y ∣ x , D ) ) x_i \leftarrow \mathop{argmax}\limits_{x \in X}S(x, p(y|x, D)) xi←x∈XargmaxS(x,p(y∣x,D))
假设的模型计算出来之后,在此模型的基础上选择满足公式(1)的参数,也就是选择 x x x。通过Acquisition Function 来选择。
Acquisition Function
1) Probability of improvement
假设 f ′ = m i n f f^{'} = min f f′=minf。
定义utility function如下:
u ( x ) = { 0 , i f f ( x ) > f ′ 1 , i f f ( x ) ≤ f ′ u(x) = \left\{ \begin{array}{rcl} 0, & & {if f(x) > f}' \\ 1, & & {if f(x) \leq f'} \end{array} \right. u(x)={0,1,iff(x)>f′iff(x)≤f′
probability of improvement acquisition function 定义为the expected utility as a function of x:
a P I = E [ u ( x ) ∣ x , D ] = ∫ − ∞ f ′ N ( f ; μ ( x ) , K ( x , x ) ) d f = Φ ( f ′ ; μ ( x ) , K ( x , x ) ) a_{PI} = E[u(x)|x, D] = \int_{-\infty}^{f'} N(f; \mu(x),K(x,x))df \\[8pt] = \Phi(f'; \mu(x), K(x,x)) aPI=E[u(x)∣x,D]=∫−∞f′N(f;μ(x),K(x,x))df=Φ(f′;μ(x),K(x,x))
求出 a ( x ) a(x) a(x) 的最大值即可求出基于高斯分布的满足要求的 x x x。
2)Expected improvement
上面的AC function 有个缺点就是找到的 x x x 可能是局部最优点,所以有了Expected improvement。
f ′ = m i n f f' = min f f′=minf
utility function定义如下:
u ( x ) = m a x ( 0 , f ′ − f ( x ) ) u(x) = max(0, f'-f(x)) u(x)=max(0,f′−f(x))
AC function 定义如下:
a E I = E [ u ( x ) ∣ x , D ] = ∫ − ∞ f ′ ( f ′ − f ) N ( f ; μ ( x ) , K ( x , x ) ) d f = ( f ′ − μ ( x ) ) Φ ( f ′ ; μ ( x ) , K ( x , x ) ) + K ( x , x ) N ( f ′ ; μ ( x ) , K ( x , x ) ) a_{EI} = E[u(x)|x, D] = \int_{-\infty}^{f'}(f' - f)N(f; \mu(x), K(x, x))df \\[8pt] =(f' - \mu(x))\Phi(f'; \mu(x), K(x, x)) + K(x, x)N(f'; \mu(x), K(x,x)) aEI=E[u(x)∣x,D]=∫−∞f′(f′−f)N(f;μ(x),K(x,x))df=(f′−μ(x))Φ(f′;μ(x),K(x,x))+K(x,x)N(f′;μ(x),K(x,x))
通过计算使得 a E I a_{EI} aEI值最大的点即为最优点。
上式有两个组成部分,使得上式最大则需要同时优化左右两个部分:
左边需要尽可能的减少 μ ( x ) \mu(x) μ(x)
右边需要尽可能的增大方差(或协方差) K ( x , x ) K(x,x) K(x,x)
但二者不能同时满足,这是一个exploration tradeoff
3)Entropy search
u ( x ) = H [ x ∗ ∣ D ] − H [ x ∗ ∣ D , x , f ( x ) ] u(x) = H[x^*|D] - H[x^*|D, x, f(x)] u(x)=H[x∗∣D]−H[x∗∣D,x,f(x)]
4)Upper confidence bound
a U C B ( x ; β ) = μ ( x ) − β σ ( x ) σ ( x ) = K ( x , x ) a_{UCB}(x;\beta) = \mu(x) - \beta\sigma(x) \\[10pt] \sigma(x) = \sqrt{K(x,x)} aUCB(x;β)=μ(x)−βσ(x)σ(x)=K(x,x)
<5>. y i ← f ( x i ) y_i \leftarrow f(x_i) yi←f(xi)
通过上述步骤选出了一组超参数 x i x_i xi, 下一步将超参数带入网络中去进行训练, 最后得到输出 y i y_i yi
<5>. D ← D ∪ ( x i , y i ) D \leftarrow D \cup(x_i, y_i) D←D∪(xi,yi) 更新数据集