吴恩达机器学习课程-第八周

1.聚类Clustering

1.1 无监督学习简介

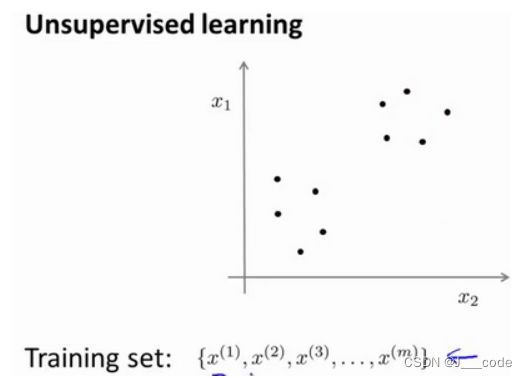
对于监督学习，训练集是有标签的，其目标是找到能够区分正样本和负样本的决策边界。而在非监督学习中，数据没有附带任何标签，如下图所示，将这些无标签的训练数据，输入到一个算法中，最终找这些数据的内在结构：

1.2 K-均值

1.2.1 算法流程

​K-均值(K-Means)算法是最普及的聚类算法，该算法需要一个未标记的数据集以及$K$值，然后将数据聚类成不同的组。具体过程如下：

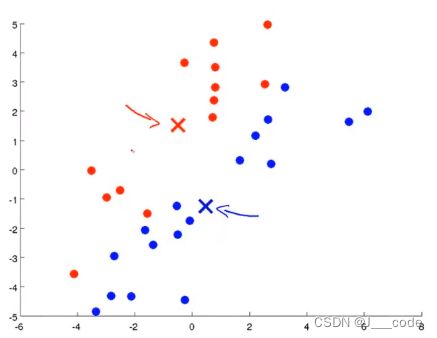
1. 随机选择$K$个随机的点，称为聚类中心（cluster centroids)

2. 对于数据集中的每一个数据，按照距离这$K$个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类

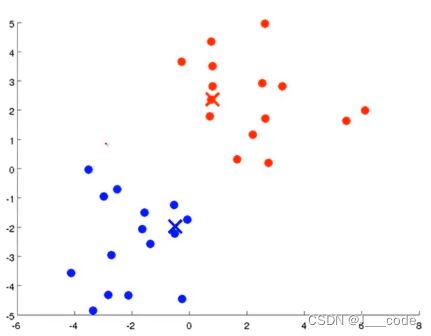
3. 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置

4. 重复步骤1-3直至中心点不再变化

如果存在没有被分到点的聚类中心，一般的解决方式是重新随机选择聚类中心点或者直接删除该中心点

1.2.2 优化目标

K-均值需要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此K-均值的代价函数为：

​ $J(c^{(1)},...c^{(m)},{\mu }_1,{\mu }_k)=\frac{1}{m}{\sum }_{i=1}^m||X^{(i)}-u_{c^{(i)}}|{|}^2$

其中$u_{c^{(i)}}$表示和$x^{(i)}$最近的聚类中心点，$c^{(i)}$表示样本$x^{(i)}$当前被分到簇的下标。最终的优化目标即：

​ $\underset{c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_k}{\min }J(c^{(1)},...c^{(m)},{\mu }_1,{\mu }_k)$

1.2.3 随机初始化

在运行K-均值算法时，首先要随机初始化所有的聚类中心点，初始化的方式如下：

• 选择的$K$要满足$K<m$，即聚类中心点的个数要小于所有训练集实例的数量
• 随机选择$K$个训练样本，然后令这$K$个聚类中心分别与这个训练实例相等

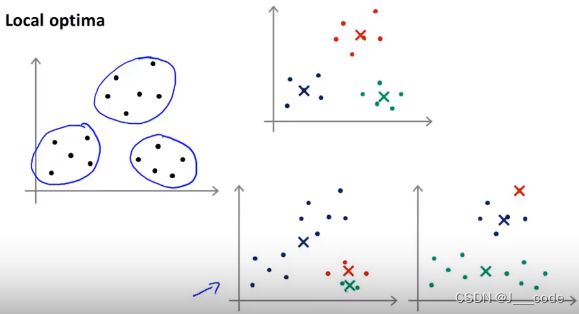
初始化的情况会决定K-均值算法最后是否会停留在局部最小值，下图中右侧的上子图较好地将训练集分为三簇，但是在下子图中分类效果并不理想，因为停留在了局部最小值：

为了解决上述问题，需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果($K$较大时可能这样做的效果也不会很好)

1.2.4 选择聚类数

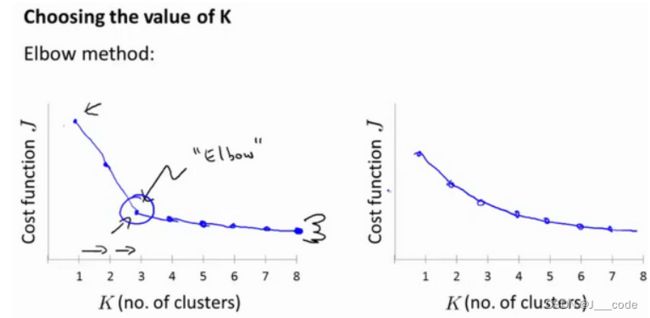
​选择的时候思考运用K-均值算法聚类的动机是什么，然后选择能最好服务于该目标的聚类数。常被讨论的方法为“肘部法则”，如下图所示，构建出$K$和目标函数$J$的图像。在左子图中，从$K=1$到$K=3$时，$J$下降的很快，但是之后变开始变得缓慢，所以可以选择肘点$K=3$。但是实际情况如右子图所示：

2.降维Dimensionality Reduction

2.1 目标一：数据压缩

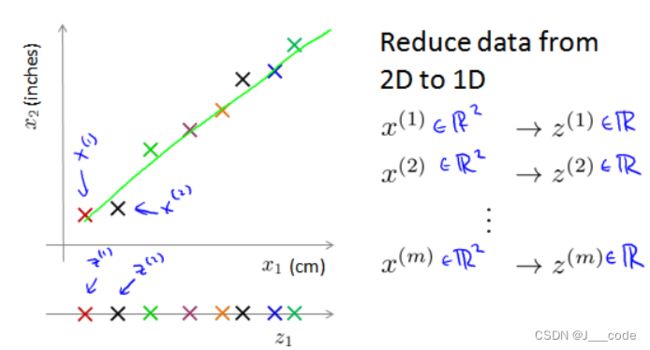
如下图所示，假设对于训练集存在两个的特征，$x_1$表示长度(cm)，$x_2$也表示长度(英寸)，这两个特征明显冗余(或者称为高度相关)。同时意味着要保存每个样本需要保存两个特征数，造成了内存的浪费。如果能将这两个特征采用一个特征$z_1$表示，就能将内存的需求减半(还能加快算法的运行)：

2.2 目标二：可视化

假使每个样本有50个特征(如GDP，人均GDP，平均寿命等)，如果要将这个50维的数据可视化是不可能的。此时可以使用降维的方法将其降至2维，这样便可将其可视化：

2.3 主成分分析PCA

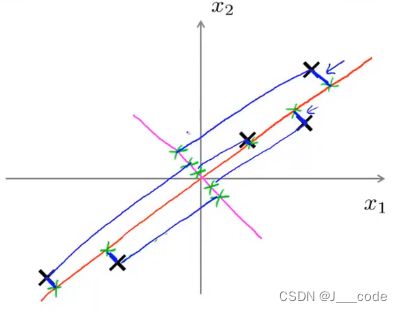
PCA中需要找到一个方向向量(Vector direction)，当把所有的数据都投射到该向量上时，希望投射平均均方误差能尽可能地小。如图所示，方向向量是一个经过原点的向量，投射误差是每个数据点(已对特征值$x_1、x_2$进行了特征规范化)对方向向量作垂线的长度(即蓝色线段的长度)。如果选择紫红色线作为方向向量，明显投射误差要大于以橘色线的投射误差：

所以要将$n$维数据降至$k$维，其目标是找到向量$u^{(1)}、u^{(2)}、...、u^{(k)}$，使得总的投射误差最小，比如要将三维数据降至二维，则找到向量$u^{(1)}、u^{(2)}$使得所有数据点到这两个向量构成的二维平面距离最小

注意主成分分析与线性回归是不同的算法，区别在于：

• 主成分分析最小化投射误差，线性回归最小化预测误差
• 线性回归的目的是预测结果，主成分分析不作任何预测

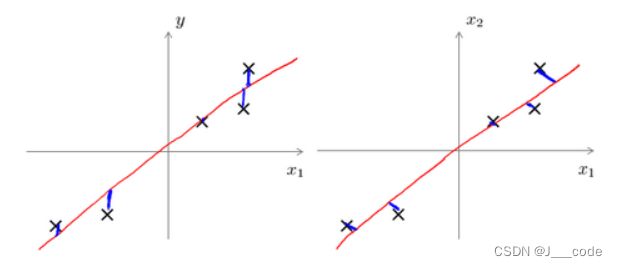
左边的是线性回归的误差(垂直于$x_1$轴投影)，右边是主要成分分析的误差(垂直于红线投影)：

2.3.1 主成分分析算法

​对于PCA的最终目的是将原来用$x_1、x_2$表示的数据转换为只用$z_1$表示的数据，这个过程该如何实现？

1. 均值归一化：令$x_j=x_j-u_j$，如果特征在不同的数量级上，还需要将其除以标准差 ${\sigma }^2$
2. 计算协方差矩阵$\sum =\frac{1}{m}{\sum }_{i=1}^m(x^{(i)})(x^{(i)}{)}^T$，$x^{(i)}\in n\times 1$且$n$为原始特征数，$m$为样本数
3. 计算协方差矩阵$\sum$的特征向量：可以利用奇异值分解SVD来求得$U、S、V$
4. 在$U\in n\times n$中选取前$k$个向量，即得到一个$n\times k$的矩阵$U_{reduce}$，利用它得到$z^{(i)}=U_{reduce}\ast x^{(i)}$且$z^{(i)}\in k\times 1$

2.3.2 选择主成分的数量

选择$k$ 的依据是平均均方误差与训练集方差的比例尽可能小，如果希望该比例小于1%(即原本数据的差异有99%都保留下来)，则不断修改$k$的值直到满足要求：

​ $\frac{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{(i)}-x_{approx}^{(i)}\Vert }^2}{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{(i)}\Vert }^2}=1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^m{S}_{ii}}\le 1\%$

​需要计算上面的式子需要获得$U_{reduce}$以及$z^{(1)}、z^{(2)},...$，然后计算$x_{approx}^{(i)}=U_{reduce}{z}^{(i)}$。也可以直接利用SVD计算得到的$S$去计算该比例是否小于$1\%$(即带入上式等号右边的公式)

2.3.3 压缩重现

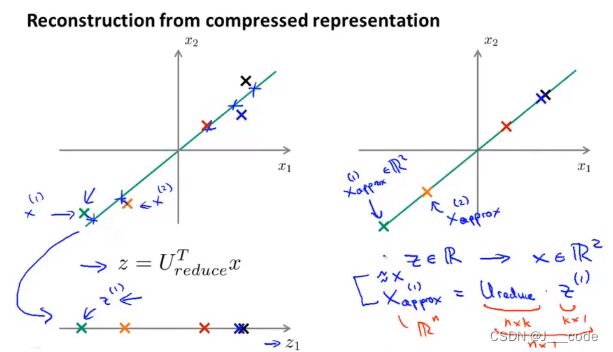
假设已经得到PCA压缩后的数$z=U_{reduce}^T\cdot x$，如何将其转换为原来高维数据的近似$x_{approx}$?$x_{approx}=U_{reduce}\cdot z$，下面右子图中的数据点即近似后的数据点：

2.3.4 PCA的应用

假如此时多张100×100像素的图片进行机器学习(即训练集为$(x^{(1)},y_1),(x^{(2)},y_2),...,(x^{(m)},y_m)$)，意味着每张图片共有10000 个特征，如果直接将所有特征放入神经网络，会导致训练速度过慢。为了加快速度，需要将其降维：

1. 将训练集的标签忽略，利用PCA将$x^{(1)}、x^{(2)}、...、x^{(m)}$转换为$z^{(1)}、z^{(2)}、...、z^{(m)}$，其中维度降为1000
2. 构建新的训练集$(z^{(1)},y_1),(z^{(2)},y_2),...,(z^{(m)},y_m)$，对其进行训练
3. 预测时，使用训练集学习的$U_{reduce}$将测试集样本$x_{t}est$转换为$z_{test}$再进行预测

将10000维降维1000维貌似获得了更少的特征，也就更不容易过拟合，所以会认为PCA是防止过拟合的方法，其实这是错误的。因为主PCA不考虑任何与结果变量有关的信息(因为进行降维时根本没用到标签值)，因此可能会丢失非常重要的特征。当进行正则化处理时会考虑到标签值，不会丢掉重要的数据

另外对于高维训练集应该先不使用PCA进行训练，如果发现速度过慢或者内存占用多大再尝试使用PCA

综上所述，PCA主要的作用为：

• 压缩数据节省内容空间
• 将数据可视化
• 加快模型训练速度

3.参考

https://www.bilibili.com/video/BV164411b7dx?p=76-87

http://www.ai-start.com/ml2014/html/week8.html