20220609学习记录（st表、动态规划、数学）

（220608学习记录 (也就是昨天做的题) 是220502 学习记录的后三道题）

B. 炸鸡块君与FIFA22

B-炸鸡块君与FIFA22

题解：

首先是st表部分，分为建表和查询两部分。参考：算法学习笔记(12): ST表 - 知乎 (zhihu.com)

Part1 st建表 

首先把所有数据都放入f[i][0]中。一代目是找到以 j 开头的，区间的最大的数，也就是拿和取最大；二代目是找到以 j 开头的，区间的最大的数，也就是拿和取最大；三代目是找到以 j 开头的，区间的最大的数，也就是拿和取最大……如此持续i遍。

int f[MAXN][21]; // f[a][b]中a是总数，b是关于区间的
for (int i = 1; i <= n; ++i)
    f[i][0] = read(); // 读入数据，自己的数据
for (int i=1;i<=20;++i)
    for (int j=1;j+(1<

Part2 st查表 

查询[ l , r ]区间时，找到这个区间的两个的子区间，它们的并集恰是[ l , r ]。目标是找到区间和区间，要求尽量靠 r，因此。

算log时的O(n)预处理：

for (int i=2;i<=n;++i)Log2[i]=Log2[i/2]+1;//Log2是数组

查询代码如下：

for (int i = 0; i < m; ++i){
    int l = read(), r = read();
    int s = Log2[r - l + 1];
    printf("%d\n", max(f[l][s],f[r-(1<

Part3 解题

首先是初始化，把每个变化量都放在三维数组里

for(int i=1;i<=n;i++){//初始化
        if(s[i]=='W')f[0][i][0]=f[1][i][0]=f[2][i][0]=1;
        if(s[i]=='L')f[1][i][0]=f[2][i][0]=-1;
    }

之后是建表，设起始分数为a，现在的分数的变化量等于 a加上一轮的分数变化量为起点的 后一半变化量。

 for (int i=1;i<=20;++i)
    for (int j=1;j+(1<

最后是查询部分，l逐渐靠近，然后把每个部分的分数都加上。

 while(q--){
        int l,r,ss;cin>>l>>r>>ss;
        int res=ss;int tmp=ss%3;
        for(int i=20;i>=0;i--){
            if((l+(1<

全部代码：

#include
using namespace std;
int f[5][200005][25];
int main()
{
    int n,q;cin>>n>>q;string s;
    cin>>s;s=" "+s;
    for(int i=1;i<=n;i++){//初始化
        if(s[i]=='W')f[0][i][0]=f[1][i][0]=f[2][i][0]=1;
        if(s[i]=='L')f[1][i][0]=f[2][i][0]=-1;
    }
    for (int i=1;i<=20;++i)
    for (int j=1;j+(1<>l>>r>>ss;
        int res=ss;int tmp=ss%3;
        for(int i=20;i>=0;i--){
            if((l+(1<

K. 冒险公社

K 冒险公社 

dp[now][i][j][k]表示当前第now个岛，i是当前岛颜色，j是前一个岛颜色，k是前前一个岛颜色。

Part1 初始化

首先是前三座岛屿初始化， 把三座岛27种可能全部都列出来，注意只有符合条件的才能放出来

 for(int i=1;i<4;i++)
    for(int j=1;j<4;j++)
    for(int k=1;k<4;k++){
        int g=0,r=0,b=0;
        if(i==1)g++;if(j==1)g++;if(k==1)g++;
        if(i==2)r++;if(j==2)r++;if(k==2)r++;
        if(i==3)b++;if(j==3)b++;if(k==3)b++;
        if(g>r&&s[3]=='G')dp[3][i][j][k]=g;//符合情况
        if(g==r&&s[3]=='B')dp[3][i][j][k]=g;
        if(g

Part2 动态规划

 把当前岛的27个情况都列出来，这个地点的状态是由上一个状态转移过来的。

设当前状态是{i j k}，根据 j k状态去找 now-1 状态的{j k l}。当 i 是绿色的时候，dp值在now-1上+1；如果不是，now的量等于now-1的量。

 for(int now=4;now<=n;now++){
        for(int i=1;i<4;i++)
        for(int j=1;j<4;j++)
        for(int k=1;k<4;k++){
            int g=0,r=0,b=0;
            if(i==1)g++;if(j==1)g++;if(k==1)g++;
            if(i==2)r++;if(j==2)r++;if(k==2)r++;
            if(i==3)b++;if(j==3)b++;if(k==3)b++;
            for(int l=1;l<=3;l++){
                if(g>r&&s[now]=='G')
                    dp[now][i][j][k]=max(dp[now][i][j][k],dp[now-1][j][k][l]+(i==1));
                if(g==r&&s[now]=='B')
                    dp[now][i][j][k]=max(dp[now][i][j][k],dp[now-1][j][k][l]+(i==1));
                if(g

最后取最大就可以了。

代码：

#include
using namespace std;
int dp[100005][4][4][4];//现在，岛现在，前一个岛，前前一个岛
int main()
{
    int n;cin>>n;
    memset(dp,-0x3f,sizeof(dp));
    string s;cin>>s;s=" "+s;
    for(int i=1;i<4;i++)
    for(int j=1;j<4;j++)
    for(int k=1;k<4;k++){
        int g=0,r=0,b=0;
        if(i==1)g++;if(j==1)g++;if(k==1)g++;
        if(i==2)r++;if(j==2)r++;if(k==2)r++;
        if(i==3)b++;if(j==3)b++;if(k==3)b++;
        if(g>r&&s[3]=='G')dp[3][i][j][k]=g;//符合情况
        if(g==r&&s[3]=='B')dp[3][i][j][k]=g;
        if(gr&&s[now]=='G')
                    dp[now][i][j][k]=max(dp[now][i][j][k],dp[now-1][j][k][l]+(i==1));
                if(g==r&&s[now]=='B')
                    dp[now][i][j][k]=max(dp[now][i][j][k],dp[now-1][j][k][l]+(i==1));
                if(g

G ACM is all you need

G-ACM is all you need

因为是对所有的函数值进行，所以后面的b其实不重要，重要的是看绝对值里面的部分。

part1 算距离求区间

找到每三个点当中最中间的点不是局部最小点的b的区间范围，其实就是计算a[i]到b的距离。

三个点是低中高三者的排列组合，一共有6种情况。如果连续的两个点高度相等，那么它们绝对不会是局部最小点，所以不用计算在内。

例如三个点是 左高中中右低 这种情况，那么此时b的选择范围有两个，分别是 到 （加1是因为b是整数，而且保证中间不是局部最小）和 到 。

但这六种情况可以通过min和max合并成3种情况，如代码所示。

Part2 计算区间覆盖最多的数

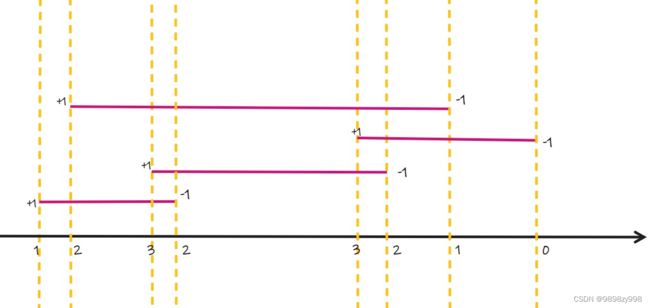
现在有很多区间，要计算区间覆盖最多的数。如下图所示，区间的左端点记为+1，右端点的下一个点记为-1，如此每个点从小到大顺下去加减，这样就能求出每个点被区间覆盖的次数。

用map实现。

Part3 求点

 可以看到，本来是局部最小点的区间都是x到正无穷，其他两种本来就不是局部极小值的点都是有负无穷到x的。

于是在计算的时候，设本来就是局部极小的点有ans个，区间覆盖的最大次数为sum。

如果取到的这个b刚好让一个不是局部极小的点p变成局部极小了，那么这个sum肯定会先对点p这个区间右端点减去1了。所以最终的答案是ans-sum。

代码：（当然还有一种解法是找出中间的点是局部极小点的区间，然后求区间覆盖的最少，但这里不做了）

#include
using namespace std;
int a[100005];
map mp;
int main()
{
 int T;cin>>T;
    while(T--){
        mp.clear();
        int n;cin>>n;int ans=0;
        for(int i=1;i<=n;i++){cin>>a[i];}
        for(int i=2;i<=n-1;i++){
            if(a[i]a[i+1]&&a[i]>a[i-1]){//防止转换后，中间的点变小了
                int r=(a[i]+max(a[i-1],a[i+1]))/2;//到无限小
                mp[r+1]--;//--方面一定是+1后计算的
            }
            else if(a[i]>a[i+1]&&a[i]a[i-1]){
                //防止转换后，中间的点变小了
                int l=(a[i]+max(a[i-1],a[i+1])+1)/2;//到无限大
                mp[l]++;
                int r=(a[i]+min(a[i-1],a[i+1]))/2;//到无限小
                mp[r+1]--;
            }
        }int res=0,sum=0,a=0;
        for(auto i:mp){res+=i.second;sum=max(sum,res);}
        cout<