Python中的时间序列分析——带有许多例子的全面导读
时间序列是在一定时间间隔内被记录下来的观测值。这篇导读会带你走进python中时间序列上的特征分析的大门。
1.什么是时间序列?
时间序列是在一定时间间隔内记录下的观测值序列。
依据观测的频率,时间序列可以是按小时的,按天的,按周的,按季度的,和按年的。有时,你甚至有秒和分的时间序列,像每分钟的点击次数和用户访问量。
为什么要分析一个时间序列?
因为那是你预测一个序列的准备步骤。
此外,序列预测有着重要的商业价值,那些像需求和销售,网站的访问人数,股票价格等等都是时间序列数据。
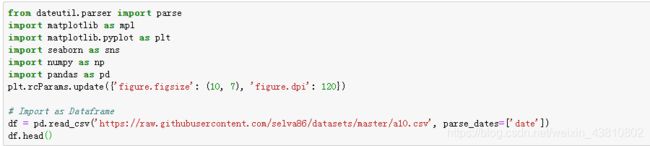
2. 如何在python中导入时间序列?
我们用 read_csv() 来读时间序列数据。加上 parse_dates=[‘date’] 参数会使得列被解析成日期属性。
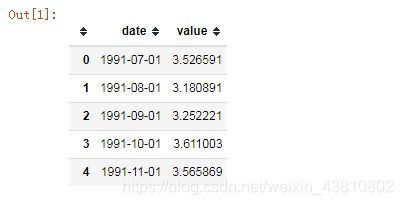
另外,你也可以把其当作Series导入,并把date作为索引。
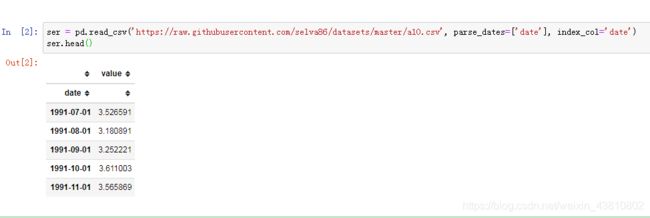
3.什么是面板数据?
面板数据也是基于时间的数据集。
区别在于,除了时间之外,它还包括一个或更多同一个时间段中测量的相关变量。
典型的,面板数据的列包含着解释性的变量,而它们对预测Y有很大帮助。
4.可视化时间序列
让我们用matplotlib来可视化时间序列吧。

因为所有的值都是正的,你可以在Y轴的两侧展现出来以表现增长性。

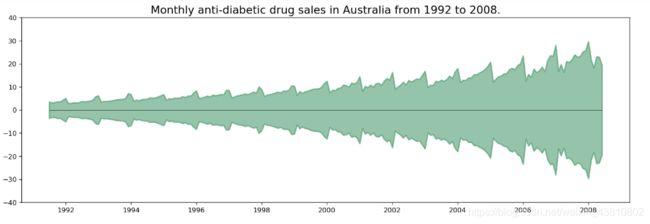
因为这是个每月的时间序列,然后每年都遵循着一定的重复的模式,你可以在同一幅图中画出每一年的图像,方便比较。
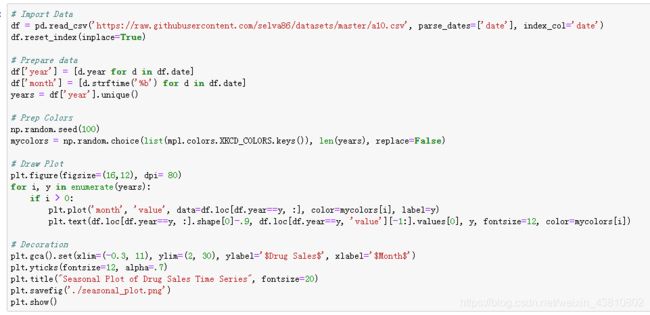
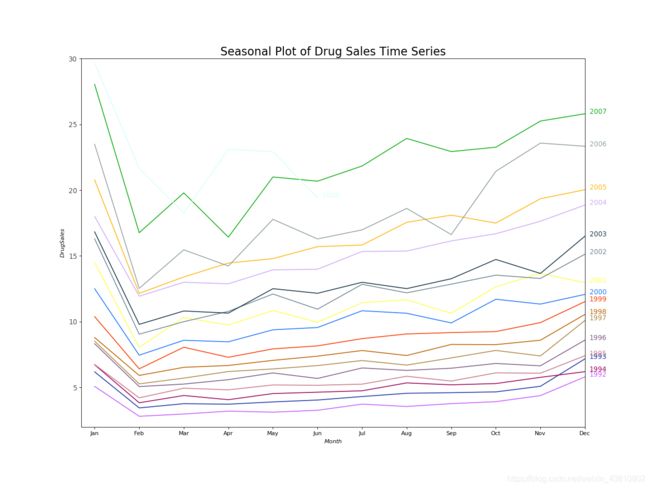
每个二月份都会有一个大的跌落,三月份又起来,四月份又掉下去,显然,这种模式在给定的一年出现,在每一年都出现。
然而,过了几年,药物销量总体在增长。你可以用年度的箱形图很好地可视化这种趋势。同样的,你也可以用一个月度箱形图来可视化每月的分布。
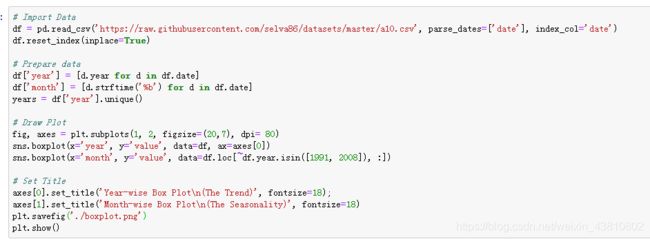
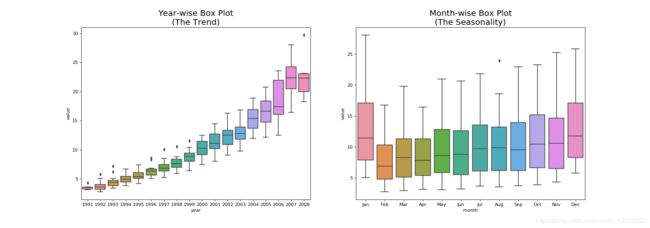
至此,我们看到了模式中的相似性。现在,如何找到一般模式中的离群值呢?
5.时间序列中的模式
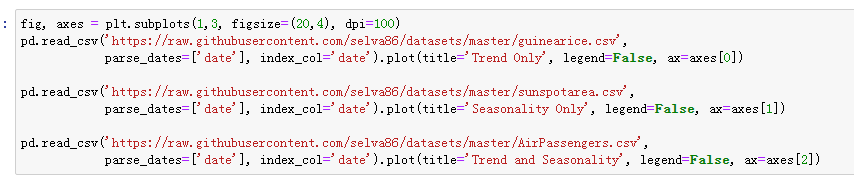
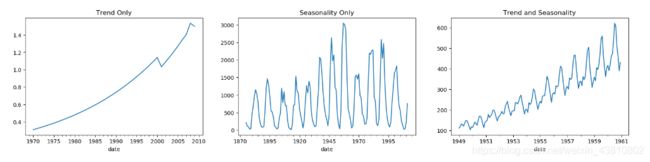
任何一个时间序列可以分成以下几个部分:基本值+趋势+季度性+误差
趋势就是在时间序列中观察到的增长或跌落的斜率。季度性就是由于季度因素在一定时间间隔内观察到的有区别的重复的模式。它可以是一年中的一个月,一个月中的一天,一天中的某个时间。
然而,所有的时间序列都有趋势或者季度性不是必须的。它可以有趋势但没有季度性,反过来也一样。
所以,一个时间序列可以想象成是趋势、季度性、误差项的组合。
 另一方面要考虑的是周期性的行为。它发生在起和落的模式不发生在固定的时间间隔上。
另一方面要考虑的是周期性的行为。它发生在起和落的模式不发生在固定的时间间隔上。
如何区分周期性和季度性呢?
如果模式不是固定日期频率的 ,那就是周期性。因为,和季度性不同,周期性往往受商业和社会经济因素影响。
6.加法和乘法时间序列
基于趋势和季度性的性质,一个时间序列可以由加法或乘法来描述,也就是要么是各个组件的加法,要么是各个组件的乘法。
加法时间序列:
价值=基础值+趋势+季度性+误差
乘法时间序列
价值=基础值×趋势×季度性×误差
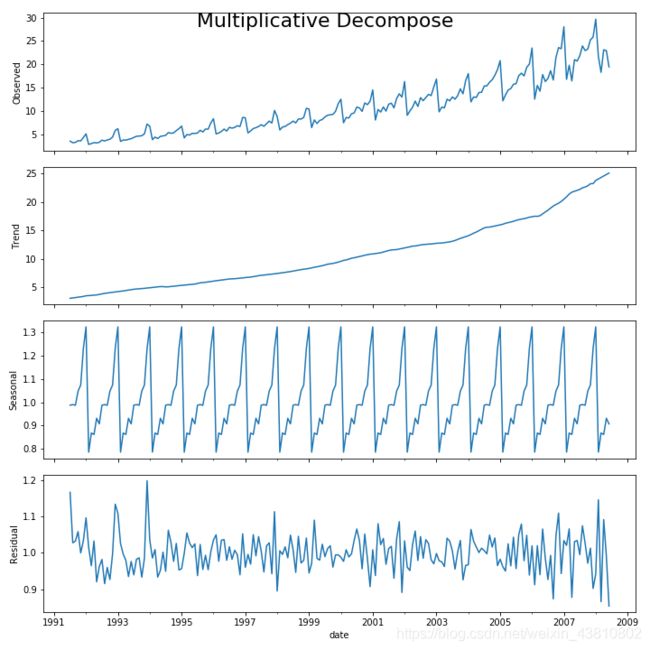
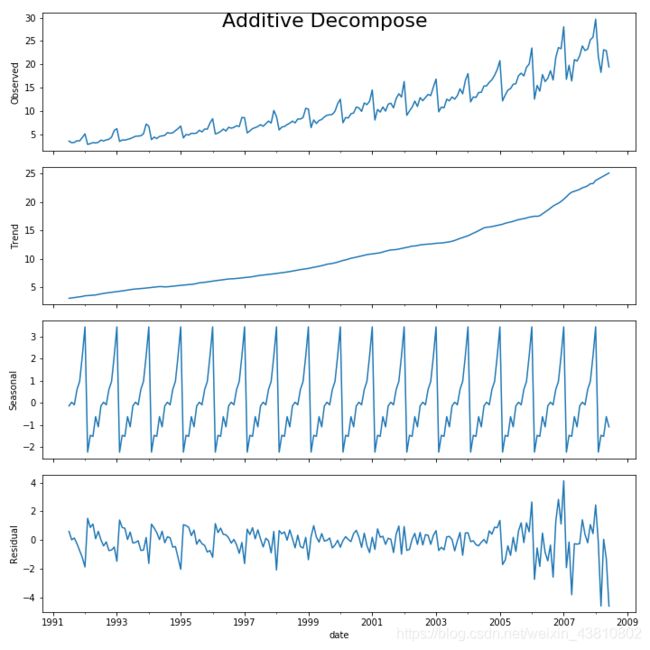
7.如何把一个时间序列分解成各个小组件呢?
statsmodels 中的 seasonal_decompose 很好实现了这一点。
设置extrapolate_trend=‘freq’ 考虑了序列开始时在趋势和残差方面缺失的值。
如果你仔细看加法分解的残差,你会发现遗留下来的一些模式。而乘法的分解,看起来很随机,当然这是好的。所以理想的,乘法分解对于这个序列是更好的。
趋势、季节性的、残差的组件的数值输出都存在result_mul中,让我们把它抽出来存在一个dataframe中吧。
8.平稳时间序列和非平稳时间序列
平稳性是时间序列的一个性质。平稳的时间序列它的值不是时间的函数。
也就是说,像均值、方差、自相关性对于时间都是常量。自相关性就是时间序列和前一个值的关联罢了。
我们等一下再说,但是要知道用一种合适的变换能够把任何序列变成平稳的。很多统计预测方法都是在处理平稳时间序列。
9.如何让时间序列平稳化?
你可以通过以下方法让序列平稳化:
1.给序列做差分(一次或多次)
2.取对数
3.开n次方
4.以上综合起来
什么是差分?
如果 Y t Y_t Yt 是在时间 t t t的值,那么一阶差分就是 Y = Y t − Y t − 1 Y=Y_t-Y_{t-1} Y=Yt−Yt−1。
比如,考虑以下序列:
[ 1 , 5 , 2 , 12 , 20 ] [1,5,2,12,20] [1,5,2,12,20]
一阶差分:
[ 5 − 1 , 2 − 5 , 12 − 2 , 20 − 12 ] = [ 4 , − 3 , 10 , 8 ] [5-1,2-5,12-2,20-12]=[4,-3,10,8] [5−1,2−5,12−2,20−12]=[4,−3,10,8]
二阶差分:
[ − 3 − 4 , 10 − ( − 3 ) , 8 − 10 ] = [ − 7 , 13 , − 2 ] [-3-4,10-(-3),8-10]=[-7,13,-2] [−3−4,10−(−3),8−10]=[−7,13,−2]
10.为什么要在预测前把非平稳化序列转成平稳化?
一个重要的原因是,自回归预测模型大多都是线性回归模型,而它们会优化序列本身的滞后性。
我们知道线性回归在X变量都互不相关时工作的最好。所以,平稳化序列解决了这个问题,因为移除了持久的自相关,以使得预测模型中序列的滞后性几乎是不相关的。
11.如何来检测平稳性?
我们会用一种叫做‘单位根检测’的方法。
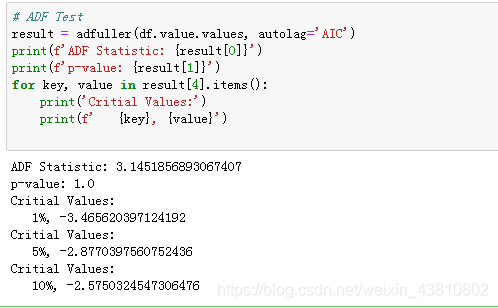
该方法包含ADH test(Augmented Dickey Fuller test )和KPSS test(Kwiatkowski-Phillips-Schmidt-Shin)。
最常用的是ADF test,它的空假设是时间序列有一个单位根并且是非平稳化的。因此,如果ADH中的P-value小于0.05,那你就拒绝空假设。
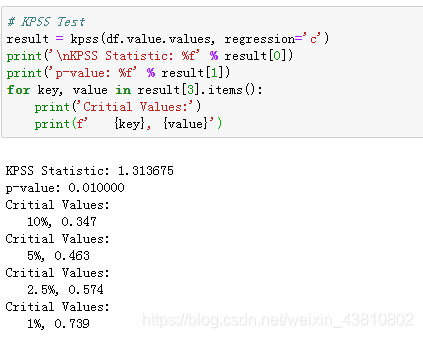
KPSS test,相反地,是用在趋势平稳化上的。空假设和P-value的解释与ADF test正好相反。
下面的代码分别实现了两种测验。
12.白色噪音和平稳化序列有什么区别?
和平稳化序列一样,白色噪音也不是一个以时间为变量的函数,也就是说,它的均值和方差不随时间而改动。区别在于,白色噪音是完全的以0为均值的随机分布。
白色噪音是没有模式的。如果你考虑FM广播的信号,频道之间你听到的空白声音就是白色噪音。
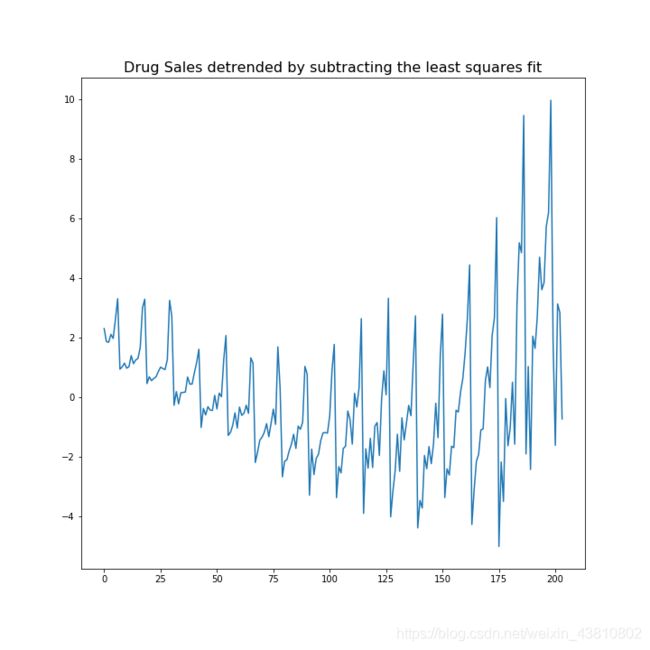
13.如何给一个时间序列去趋势化?
去趋势化就是把时间序列中的趋势组件移除掉。但是如何提取趋势呢?这里有很多方法。
1.从时间序列中减去最佳拟合曲线。最佳拟合曲线可以用线性回归模型得到。
2.从时间序列中拿到趋势组件,就像我们之前看到的,然后减去。
3.减掉平均值。
让我们来实现前两种方法。
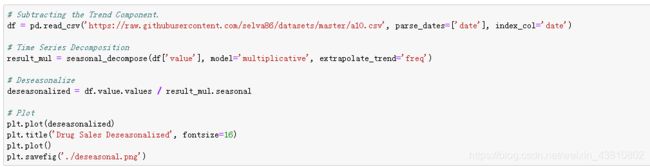
14.如何在时间序列中去掉季度性?
1.用长度取移动平均,作为季度窗口。这会在过程中使序列平滑。
2.序列中作季度差分
3.用STL分解中得到的季度索引去除序列
如果除以季度索引不是很好的话,那就对序列取对数然后再去季度化。之后你再求它的指数来还原原始大小。
15.如何测试一个时间序列的季度性?
通常的方法是画出时间序列然后看一看特定时间间隔内重复的模式。因此,季度性的类型由钟表或日历决定。
1.一天中的小时
2.一月中的天数
3.每周
4.每月
5.每年
然而,如果你想要一个更加定义化的观察,那就使用自相关函数(ACF)。由于有强烈的季度性,ACF图像会展现出重复的尖头,在季度窗口的许多地方。
比如,药物销售时间序列是一个月度时间序列,每年重复,因此你可以在第12,第24,第36……处看到尖头。
15.如何在时间序列中对待缺失值?
有时候,你的时间序列会有缺失值。
你不能用时间序列的均值去替代那些缺失值,尤其是序列未平稳。快速的方法是用之前的值填充。
其他一些有效的方法:
- 往前填充
- 线性插值
- 二次插值
- 最邻均值
- 季度性均值
为了测试缺失值填充的性能,我手动制造了一些缺失值,用以上方法来填充,并测量原始值和插值的均方误差.
原始值:
“date”,“value”
1991-07-01,3.526591
1991-08-01,3.180891
1991-09-01,3.252221
1991-10-01,3.611003
1991-11-01,3.565869
1991-12-01,4.306371
1992-01-01,5.088335
1992-02-01,2.81452
1992-03-01,2.985811
1992-04-01,3.20478
1992-05-01,3.127578
1992-06-01,3.270523
1992-07-01,3.73785082
1992-08-01,3.55877609
1992-09-01,3.77720173
1992-10-01,3.92449042
1992-11-01,4.38653092
1992-12-01,5.81054917
1993-01-01,6.19206769
1993-02-01,3.45085699
1993-03-01,3.77230686
1993-04-01,3.7343029
1993-05-01,3.90539892
1993-06-01,4.04968714
1993-07-01,4.31556552
1993-08-01,4.56218455
1993-09-01,4.60866203
1993-10-01,4.66785129
1993-11-01,5.09384145
1993-12-01,7.1799622
1994-01-01,6.73147308
1994-02-01,3.84127758
1994-03-01,4.39407557
1994-04-01,4.07534073
1994-05-01,4.5406449
1994-06-01,4.64561508
1994-07-01,4.75260653
1994-08-01,5.35060467
1994-09-01,5.20445484
1994-10-01,5.3016513
1994-11-01,5.77374216
1994-12-01,6.20459348
1995-01-01,6.74948382
1995-02-01,4.21606735
1995-03-01,4.94934946
1995-04-01,4.8230449
1995-05-01,5.19475419
1995-06-01,5.17078711
1995-07-01,5.25674157
1995-08-01,5.85527729
1995-09-01,5.49072901
1995-10-01,6.11529323
1995-11-01,6.08847284
1995-12-01,7.41659792
1996-01-01,8.32945212
1996-02-01,5.06979585
1996-03-01,5.26255667
1996-04-01,5.59712628
1996-05-01,6.110296
1996-06-01,5.68916084
1996-07-01,6.48684933
1996-08-01,6.30056933
1996-09-01,6.46747574
1996-10-01,6.82862939
1996-11-01,6.64907826
1996-12-01,8.60693721
1997-01-01,8.52447101
1997-02-01,5.27791837
1997-03-01,5.71430345
1997-04-01,6.21452908
1997-05-01,6.41192919
1997-06-01,6.66771564
1997-07-01,7.05083102
1997-08-01,6.70491861
1997-09-01,7.25098761
1997-10-01,7.81973318
1997-11-01,7.39810106
1997-12-01,10.09623339
1998-01-01,8.79851303
1998-02-01,5.91826076
1998-03-01,6.53449298
1998-04-01,6.67573561
1998-05-01,7.06420058
1998-06-01,7.38338118
1998-07-01,7.81349587
1998-08-01,7.43189221
1998-09-01,8.27511722
1998-10-01,8.26044138
1998-11-01,8.59615575
1998-12-01,10.55893902
1999-01-01,10.3914156
1999-02-01,6.42153456
1999-03-01,8.06261937
1999-04-01,7.2977391
1999-05-01,7.93691594
1999-06-01,8.16532298
1999-07-01,8.71742046
1999-08-01,9.07096378
1999-09-01,9.17711337
1999-10-01,9.25188674
1999-11-01,9.93313643
1999-12-01,11.53297428
2000-01-01,12.51146235
2000-02-01,7.45719853
2000-03-01,8.59119084
2000-04-01,8.47400037
2000-05-01,9.3868026
2000-06-01,9.56039945
2000-07-01,10.8342948
2000-08-01,10.64375083
2000-09-01,9.90816186
2000-10-01,11.7100413
2000-11-01,11.34015074
2000-12-01,12.07913184
2001-01-01,14.49758109
2001-02-01,8.04927477
2001-03-01,10.31289116
2001-04-01,9.75335821
2001-05-01,10.85038183
2001-06-01,9.96171916
2001-07-01,11.44360144
2001-08-01,11.65923889
2001-09-01,10.64705979
2001-10-01,12.65213444
2001-11-01,13.67446631
2001-12-01,12.96573509
2002-01-01,16.30026927
2002-02-01,9.05348536
2002-03-01,10.00244879
2002-04-01,10.78875007
2002-05-01,12.10670515
2002-06-01,10.95410107
2002-07-01,12.84456587
2002-08-01,12.19649985
2002-09-01,12.85474787
2002-10-01,13.54200436
2002-11-01,13.28764
2002-12-01,15.13491784
2003-01-01,16.82834968
2003-02-01,9.80021461
2003-03-01,10.81699371
2003-04-01,10.65422256
2003-05-01,12.51232269
2003-06-01,12.16120969
2003-07-01,12.9980462
2003-08-01,12.51727568
2003-09-01,13.26865761
2003-10-01,14.73362169
2003-11-01,13.66938174
2003-12-01,16.50396561
2004-01-01,18.00376795
2004-02-01,11.93802987
2004-03-01,12.9979001
2004-04-01,12.88264507
2004-05-01,13.94344681
2004-06-01,13.9894722
2004-07-01,15.33909742
2004-08-01,15.37076394
2004-09-01,16.142005
2004-10-01,16.685754
2004-11-01,17.636728
2004-12-01,18.869325
2005-01-01,20.778723
2005-02-01,12.154552
2005-03-01,13.402392
2005-04-01,14.459239
2005-05-01,14.795102
2005-06-01,15.705248
2005-07-01,15.82955
2005-08-01,17.554701
2005-09-01,18.100864
2005-10-01,17.496668
2005-11-01,19.347265
2005-12-01,20.031291
2006-01-01,23.486694
2006-02-01,12.536987
2006-03-01,15.467018
2006-04-01,14.233539
2006-05-01,17.783058
2006-06-01,16.291602
2006-07-01,16.980282
2006-08-01,18.612189
2006-09-01,16.623343
2006-10-01,21.430241
2006-11-01,23.575517
2006-12-01,23.334206
2007-01-01,28.038383
2007-02-01,16.763869
2007-03-01,19.792754
2007-04-01,16.427305
2007-05-01,21.000742
2007-06-01,20.681002
2007-07-01,21.83489
2007-08-01,23.93020353
2007-09-01,22.93035694
2007-10-01,23.26333992
2007-11-01,25.25003022
2007-12-01,25.80609
2008-01-01,29.665356
2008-02-01,21.654285
2008-03-01,18.264945
2008-04-01,23.107677
2008-05-01,22.91251
2008-06-01,19.43174
带有缺失值的数据:
“date”,“value”
1991-07-01,3.526591
1991-08-01,
1991-09-01,3.252221
1991-10-01,3.611003
1991-11-01,
1991-12-01,4.306371
1992-01-01,5.088335
1992-02-01,2.81452
1992-03-01,2.985811
1992-04-01,3.20478
1992-05-01,
1992-06-01,3.270523
1992-07-01,3.73785082
1992-08-01,
1992-09-01,
1992-10-01,3.92449042
1992-11-01,4.38653092
1992-12-01,5.81054917
1993-01-01,6.19206769
1993-02-01,
1993-03-01,3.77230686
1993-04-01,3.7343029
1993-05-01,
1993-06-01,4.04968714
1993-07-01,4.31556552
1993-08-01,4.56218455
1993-09-01,
1993-10-01,4.66785129
1993-11-01,5.09384145
1993-12-01,7.1799622
1994-01-01,6.73147308
1994-02-01,
1994-03-01,4.39407557
1994-04-01,4.07534073
1994-05-01,4.5406449
1994-06-01,4.64561508
1994-07-01,4.75260653
1994-08-01,5.35060467
1994-09-01,5.20445484
1994-10-01,5.3016513
1994-11-01,5.77374216
1994-12-01,6.20459348
1995-01-01,6.74948382
1995-02-01,
1995-03-01,4.94934946
1995-04-01,4.8230449
1995-05-01,5.19475419
1995-06-01,5.17078711
1995-07-01,5.25674157
1995-08-01,
1995-09-01,5.49072901
1995-10-01,6.11529323
1995-11-01,6.08847284
1995-12-01,7.41659792
1996-01-01,
1996-02-01,5.06979585
1996-03-01,5.26255667
1996-04-01,5.59712628
1996-05-01,6.110296
1996-06-01,5.68916084
1996-07-01,
1996-08-01,6.30056933
1996-09-01,6.46747574
1996-10-01,6.82862939
1996-11-01,
1996-12-01,8.60693721
1997-01-01,8.52447101
1997-02-01,
1997-03-01,5.71430345
1997-04-01,6.21452908
1997-05-01,6.41192919
1997-06-01,
1997-07-01,7.05083102
1997-08-01,6.70491861
1997-09-01,7.25098761
1997-10-01,
1997-11-01,7.39810106
1997-12-01,10.09623339
1998-01-01,8.79851303
1998-02-01,
1998-03-01,6.53449298
1998-04-01,6.67573561
1998-05-01,
1998-06-01,7.38338118
1998-07-01,7.81349587
1998-08-01,
1998-09-01,8.27511722
1998-10-01,8.26044138
1998-11-01,8.59615575
1998-12-01,
1999-01-01,10.3914156
1999-02-01,6.42153456
1999-03-01,8.06261937
1999-04-01,7.2977391
1999-05-01,7.93691594
1999-06-01,8.16532298
1999-07-01,8.71742046
1999-08-01,9.07096378
1999-09-01,9.17711337
1999-10-01,9.25188674
1999-11-01,9.93313643
1999-12-01,11.53297428
2000-01-01,12.51146235
2000-02-01,7.45719853
2000-03-01,8.59119084
2000-04-01,8.47400037
2000-05-01,9.3868026
2000-06-01,9.56039945
2000-07-01,10.8342948
2000-08-01,10.64375083
2000-09-01,9.90816186
2000-10-01,
2000-11-01,11.34015074
2000-12-01,12.07913184
2001-01-01,14.49758109
2001-02-01,8.04927477
2001-03-01,10.31289116
2001-04-01,9.75335821
2001-05-01,10.85038183
2001-06-01,9.96171916
2001-07-01,11.44360144
2001-08-01,11.65923889
2001-09-01,10.64705979
2001-10-01,12.65213444
2001-11-01,13.67446631
2001-12-01,12.96573509
2002-01-01,16.30026927
2002-02-01,9.05348536
2002-03-01,10.00244879
2002-04-01,10.78875007
2002-05-01,12.10670515
2002-06-01,10.95410107
2002-07-01,12.84456587
2002-08-01,12.19649985
2002-09-01,12.85474787
2002-10-01,13.54200436
2002-11-01,13.28764
2002-12-01,15.13491784
2003-01-01,16.82834968
2003-02-01,9.80021461
2003-03-01,10.81699371
2003-04-01,10.65422256
2003-05-01,12.51232269
2003-06-01,12.16120969
2003-07-01,12.9980462
2003-08-01,12.51727568
2003-09-01,13.26865761
2003-10-01,14.73362169
2003-11-01,13.66938174
2003-12-01,16.50396561
2004-01-01,18.00376795
2004-02-01,11.93802987
2004-03-01,12.9979001
2004-04-01,12.88264507
2004-05-01,13.94344681
2004-06-01,13.9894722
2004-07-01,15.33909742
2004-08-01,15.37076394
2004-09-01,16.142005
2004-10-01,16.685754
2004-11-01,17.636728
2004-12-01,18.869325
2005-01-01,20.778723
2005-02-01,12.154552
2005-03-01,13.402392
2005-04-01,14.459239
2005-05-01,14.795102
2005-06-01,15.705248
2005-07-01,15.82955
2005-08-01,17.554701
2005-09-01,18.100864
2005-10-01,17.496668
2005-11-01,19.347265
2005-12-01,20.031291
2006-01-01,23.486694
2006-02-01,12.536987
2006-03-01,15.467018
2006-04-01,14.233539
2006-05-01,17.783058
2006-06-01,16.291602
2006-07-01,16.980282
2006-08-01,18.612189
2006-09-01,16.623343
2006-10-01,21.430241
2006-11-01,
2006-12-01,23.334206
2007-01-01,28.038383
2007-02-01,16.763869
2007-03-01,19.792754
2007-04-01,16.427305
2007-05-01,21.000742
2007-06-01,20.681002
2007-07-01,21.83489
2007-08-01,23.93020353
2007-09-01,
2007-10-01,23.26333992
2007-11-01,25.25003022
2007-12-01,25.80609
2008-01-01,29.665356
2008-02-01,21.654285
2008-03-01,18.264945
2008-04-01,23.107677
2008-05-01,
2008-06-01,19.43174
fig, axes = plt.subplots(7, 1, sharex=True, figsize=(10, 12))
plt.rcParams.update({'xtick.bottom' : False})
## 1. Actual -------------------------------
df_orig.plot(title='Actual', ax=axes[0], label='Actual', color='red', style=".-")
df.plot(title='Actual', ax=axes[0], label='Actual', color='green', style=".-")
axes[0].legend(["Missing Data", "Available Data"])
## 2. Forward Fill --------------------------
df_ffill = df.ffill()
error = np.round(mean_squared_error(df_orig['value'], df_ffill['value']), 2)
df_ffill['value'].plot(title='Forward Fill (MSE: ' + str(error) +")", ax=axes[1], label='Forward Fill', style=".-")
## 3. Backward Fill -------------------------
df_bfill = df.bfill()
error = np.round(mean_squared_error(df_orig['value'], df_bfill['value']), 2)
df_bfill['value'].plot(title="Backward Fill (MSE: " + str(error) +")", ax=axes[2], label='Back Fill', color='firebrick', style=".-")
## 4. Linear Interpolation ------------------
df['rownum'] = np.arange(df.shape[0])
df_nona = df.dropna(subset = ['value'])
f = interp1d(df_nona['rownum'], df_nona['value'])
df['linear_fill'] = f(df['rownum'])
error = np.round(mean_squared_error(df_orig['value'], df['linear_fill']), 2)
df['linear_fill'].plot(title="Linear Fill (MSE: " + str(error) +")", ax=axes[3], label='Cubic Fill', color='brown', style=".-")
## 5. Cubic Interpolation --------------------
f2 = interp1d(df_nona['rownum'], df_nona['value'], kind='cubic')
df['cubic_fill'] = f2(df['rownum'])
error = np.round(mean_squared_error(df_orig['value'], df['cubic_fill']), 2)
df['cubic_fill'].plot(title="Cubic Fill (MSE: " + str(error) +")", ax=axes[4], label='Cubic Fill', color='red', style=".-")
# Interpolation References:
# https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html
# https://docs.scipy.org/doc/scipy/reference/interpolate.html
## 6. Mean of 'n' Nearest Past Neighbors ------
def knn_mean(ts, n):
out = np.copy(ts)
for i, val in enumerate(ts):
if np.isnan(val):
n_by_2 = np.ceil(n/2)
lower = np.max([0, int(i-n_by_2)])
upper = np.min([len(ts)+1, int(i+n_by_2)])
ts_near = np.concatenate([ts[lower:i], ts[i:upper]])
out[i] = np.nanmean(ts_near)
return out
df['knn_mean'] = knn_mean(df.value.values, 8)
error = np.round(mean_squared_error(df_orig['value'], df['knn_mean']), 2)
df['knn_mean'].plot(title="KNN Mean (MSE: " + str(error) +")", ax=axes[5], label='KNN Mean', color='tomato', alpha=0.5, style=".-")
## 7. Seasonal Mean ----------------------------
def seasonal_mean(ts, n, lr=0.7):
"""
Compute the mean of corresponding seasonal periods
ts: 1D array-like of the time series
n: Seasonal window length of the time series
"""
out = np.copy(ts)
for i, val in enumerate(ts):
if np.isnan(val):
ts_seas = ts[i-1::-n] # previous seasons only
if np.isnan(np.nanmean(ts_seas)):
ts_seas = np.concatenate([ts[i-1::-n], ts[i::n]]) # previous and forward
out[i] = np.nanmean(ts_seas) * lr
return out
df['seasonal_mean'] = seasonal_mean(df.value, n=12, lr=1.25)
error = np.round(mean_squared_error(df_orig['value'], df['seasonal_mean']), 2)
df['seasonal_mean'].plot(title="Seasonal Mean (MSE: " + str(error) +")", ax=axes[6], label='Seasonal Mean', color='blue', alpha=0.5, style=".-")
17.什么是自相关和偏自相关函数?
自相关就是时间序列和自身滞后的关联。如果一个序列是相当自相关的,那么,序列之前的值会对之后的值的预测有很大帮助。
偏自相关也传达了类似的信息,但是它传达的是纯粹的序列与其滞后的关联,将中间滞后带来的关联贡献排除了。


18.如何计算偏自相关函数?
那么如何去计算偏自相关函数呢?
一个序列的lag[k]的偏自相关函数是Y的自回归方程中的滞后系数。
Y的自回归方程就是Y的线性回归,并且带上自己的滞后作为预测值。
比如,如果 Y t Y_t Yt是当前序列, Y t − 1 Y_{t-1} Yt−1是一次滞后序列,那么3次滞后序列的偏自相关就是 Y t − 3 Y_{t-3} Yt−3的系数 α 3 \alpha_3 α3:
Y t = α 0 + α 1 Y t − 1 + α 2 Y t − 2 + α 3 Y t − 3 Y_t=\alpha_0+\alpha_1Y_{t-1}+\alpha_2Y_{t-2}+\alpha_3Y_{t-3} Yt=α0+α1Yt−1+α2Yt−2+α3Yt−3
19.滞后绘图
滞后图就是时间序列和它的滞后的散点图。它通常是用来检测自相关性的。如果有像一下你会看到的任何模式,序列是自相关的,如果没有这种模式,那么序列很可能就是随机的白色噪音。
下面日斑区域的序列中,n阶滞后越大,散点散的越开。
from pandas.plotting import lag_plot
plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})
# Import
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
# Plot
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Drug Sales', y=1.05)
plt.show()
19.如何估计时间序列的预测性?
时间序列越有规律,则越好预测。‘趋近熵’可以用来量化时间序列波动中的规律性和不可预测性。
趋近熵越高,则越不好预测。
样本熵和趋近熵差不多,但估计复杂度则更一致,即使对于小容量的时间序列。
# https://en.wikipedia.org/wiki/Approximate_entropy
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
rand_small = np.random.randint(0, 100, size=36)
rand_big = np.random.randint(0, 100, size=136)
def ApEn(U, m, r):
"""Compute Aproximate entropy"""
def _maxdist(x_i, x_j):
return max([abs(ua - va) for ua, va in zip(x_i, x_j)])
def _phi(m):
x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x]
return (N - m + 1.0)**(-1) * sum(np.log(C))
N = len(U)
return abs(_phi(m+1) - _phi(m))
print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.651
print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.537
print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143
print(ApEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 0.716
# https://en.wikipedia.org/wiki/Sample_entropy
def SampEn(U, m, r):
"""Compute Sample entropy"""
def _maxdist(x_i, x_j):
return max([abs(ua - va) for ua, va in zip(x_i, x_j)])
def _phi(m):
x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))]
return sum(C)
N = len(U)
return -np.log(_phi(m+1) / _phi(m))
print(SampEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.78
print(SampEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.41
print(SampEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 1.79
print(SampEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 2.42
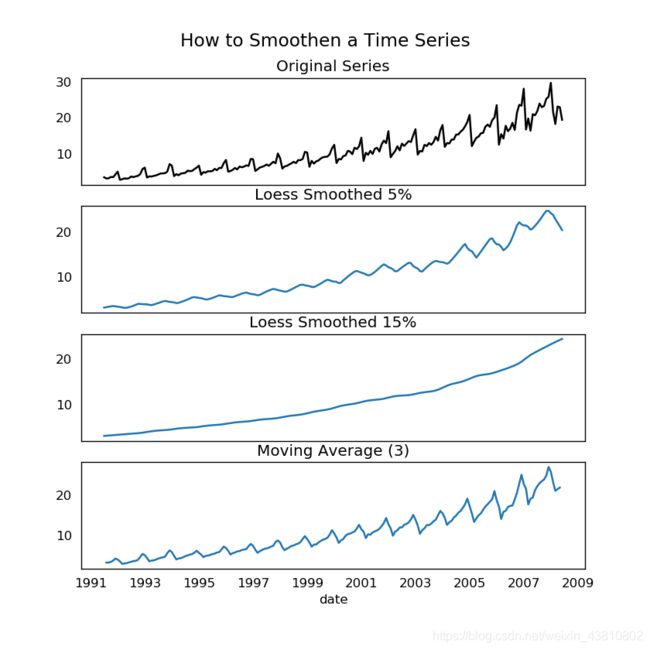
21.为什么及何如使时间序列平滑?
平滑一个时间序列的好处:
- 降低信号噪音的影响
- 平滑版的序列可以作为原始序列的一个特征解释
- 可视化趋势更简单
如何做?
1.取移动平均
2.做一个LOESS平滑(局部回归)
3.做一个LOWESS平滑(局部权重回归)
移动平均就是一定长度下的滚动窗口的平均。但是你要好好选择窗口的长度,因为大的窗口会使序列过平滑。比如,取等于季度长度的窗口大小(比方是12个月),这会使季度影响消失。
LOESS,是‘local regression’的简写。它在statsmodels包中实现,你可以用frac 参数控制平滑度,它确定了附近数据点的百分数,以将其拟合一个回归模型。
from statsmodels.nonparametric.smoothers_lowess import lowess
plt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})
# Import
df_orig = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
# 1. Moving Average
df_ma = df_orig.value.rolling(3, center=True, closed='both').mean()
# 2. Loess Smoothing (5% and 15%)
df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])
df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])
# Plot
fig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)
df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')
df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')
df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')
df_ma.plot(ax=axes[3], title='Moving Average (3)')
fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)
plt.show()