【Matlab】符号计算
符号计算
符号对象
符号对象的建立
sym函数
sym函数用于建立单个符号对象,其常用调用格式为:符号对象名=sym(A)
参数解释:
A可以是一个数值常量、数值矩阵或数值表达式(不加单引号),此时符号对象为一个符号常量;
A也可以是一个变量名(加单引号),这时符号对象为一个符号变量。
t=sym(2);
t+1/2 % 5/2
sin(sym(pi/3)) % 3^(1/2)/2
sin(pi/3) % 0.8660
a=5;
b=-8;
x=sym('a');
y=sym('b');
w=(a+b)*(a-b) % -39
s=(x+y)*(x-y) % (a + b)*(a - b)
从这里我们可以看出,用符号对象进行计算更像是一种演算和推理,得到的是一个精确的数学表达式;而数值计算的结果通常是一个数值。
syms函数
syms命令可以一次定义多个符号变量,其一般调用格式如下:syms 符号变量名1 符号变量名2 …… 符号变量名n
其中,变量名不能加单引号,相互之间用空格隔开。
syms a b c
符号对象的运算
四则运算
符号表达式的四则运算与数值运算一件,+、-、*、 /、^运算符实现,其运算结果依然是一个符号表达式。
syms x;
f=2*x^2+3*x-5;
g=x^2-x+7;
f+g % 3*x^2 + 2*x + 2,将同次项系数相加
关系运算
6种关系运算符:<、<=、>、>=、==、~=
对应的6个函数:lt( )、le( )、gt( )、ge( )、eq( )、ne( )。
若参与运算的是符号表达式,其结果是一个符号关系表达式;
若参与运算的是符号矩阵,其结果是由符号关系表达式组成的矩阵。
在进行符号对象的运算前,可用assume函数对符号对象设置值域,函数调用格式为:
-
assume(condition)
-
assume(expr,set)
第一种格式指定变量满足条件condition,第二种格式指定表达式expr属于集合set。
syms x;
assume(x<0);
abs(x)==x % -x == x
assume(x,'positive');
abs(x)==x % x == x
逻辑运算
3种逻辑运算符:&(与)、I(或)和~(非)
4个逻辑运算函数:and( )、or( )、not()和xor( )。
syms x;
y=x>0 & x<10
y=and(x>0,x<10)
% 二者结果均为:0 < x & x < 10
因式分解与展开运算
MATLAB提供了对符号表达式进行因式分解、展开、合并的函数,函数的调用格式为:
- factor(s):对符号表达式s分解因式
- expand(s):对符号表达式s进行展开
- collect(s):对符号表达式s合并同类项
- collect(s,v):对符号表达式s按变量v合并同类项
syms a b;
s=a^3-b^3;
factor(s) % [ a - b, a^2 + a*b + b^2] % 因式分解后的每一项
factor(12) % 2 2 3 % 分解质因子
我们可以利用factor函数判断一个数是否为素数。
其他运算
-
提取有理分式的分子分母:[n,d]=numden(s)
-
提取符号表达式的系数:c=coeffs(s,x)
-
符号表达式化简: simplify(s)
-
符号多项式与多项式系数向量之间的转换:
符号多项式转换为多项式系数向量:p=sym2poly(s)
多项式系数向量转换为符号多项式:s=poly2sym§
syms a b c x;
f=a*x^2+b*x+c;
g=coeffs(f,x) % 得到的系数的排列顺序是从低次到高次,与多项式系数向量排列顺序相反
g=g(end:-1:1) % 逆序
roots(g) % 求根
g =
[ c, b, a]
g =
[ a, b, c]
ans =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a)
-(b - (b^2 - 4*a*c)^(1/2))/(2*a)
符号运算中变量的确定
- 如果没有明确指定自变量,MATLAB将按以下原则确定主变量并对其进行相应运算:
- 寻找除i、j之外,在字母顺序上最接近x的小写字母。
- 若表达式中有两个符号变量与x的距离相等,则ASCII码大者优先。
-
symvar()函数可以用于查找一个符号表达式中的符号变量,函数的调用格式为:symvar(s,n)
函数返回符号表达式s中的n个符号变量。因此,可以用symvar(s,1)查找表达式s的主变量。
符号矩阵
符号矩阵也是一种符号表达式,所以符号表达式运算都可以在矩阵意义下进行。
注意:这些函数作用于符号矩阵时,是分别作用于矩阵的每一个元素。
建立符号矩阵并化简:
m = [ a 3 − b 3 s i n 2 α + c o s 2 α 15 x y − 3 x 2 x − 5 y 78 ] m= \left[ \begin{matrix} a^3-b^3 & sin^2\alpha+cos^2\alpha \\ \frac{15xy-3x^2}{x-5y} & 78 \\ \end{matrix} \right] m=[a3−b3x−5y15xy−3x2sin2α+cos2α78]
syms a b x y alp;
m=[a^3-b^3,sin(alp)^2+cos(alp)^2;(15*x*y-3*x^2)/(x-5*y),78]
simplify(m) % 化简
m =
[ a^3 - b^3, cos(alp)^2 + sin(alp)^2]
[ (- 3*x^2 + 15*y*x)/(x - 5*y), 78]
ans =
[ a^3 - b^3, 1]
[ -3*x, 78]
由于符号矩阵也是一个矩阵,所以有关矩阵的运算对符号矩阵也仍然适用,前面提到的所有有关矩阵的运算对符号矩阵也仍然适用。比如,应用于数值矩阵的点运算符和相关函数diag、inv、det、rank、trace等等,都可以直接应用于符号矩阵
当 λ \lambda λ取何值时,以下齐次线性方程组有非零解:
Cannot read properties of undefined (reading 'type')
对于齐次线性方程组 A x = O Ax=O Ax=O,当 r a n k ( A ) < n rank(A)
利用 ∣ A ∣ = 0 |A|=0 ∣A∣=0求解该问题。
syms lamda;
A=[ 1-lamda,-2,4;2,3-lamda,1;1,1,1-lamda];
D=det(A);
factor(D)
结果如下:
ans =
[ -1, lamda, lamda - 2, lamda - 3]
从结果中得知,当 λ = 0 \lambda=0 λ=0、 λ = 2 \lambda=2 λ=2或 λ = 3 \lambda=3 λ=3时,原方程组有非零解。
符号微积分
符号函数的极限
求符号函数极限的命令为limit,其调用格式为:limit(f,x,a),即求函数f关于变量x在a点的极限。
若x省略,则采用系统默认的自变量。a的默认值为0。
当左极限与右极限不相等时,limit函数的另一种功能是求单边极限,其调用格式为:
limit(f,x,a, ‘right’) 或 limit(f,x,a ,‘left’)
求下列极限
(1) lim x → a x m − a m x − a \lim_{x \to a} {\frac{\sqrt[m]{x}-\sqrt[m]{a}}{x-a}} limx→ax−amx−ma
(2) lim n → ∞ ( 1 + 1 n ) n \lim_{n \to \infty} ({1+\frac{1}{n}})^n limn→∞(1+n1)n
syms a m x n;
f=(x^(1/m)-a^(1/m))/(x-a); % (1)
limit(f,x,a)
g=(1+1/n)^n; % (2)
limit(g,n,inf)
结果如下:
ans =
a^(1/m - 1)/m
ans =
exp(1)
符号函数的导数
MATLAB中的求导函数为:diff(f,x,n)
求函数f关于变量x的n阶导数。参数x的用法同求极限函数limit,可以缺省,默认值与limit相同,n的默认值是1。
在符号函数中的变量多于一个的情况下,diff函数也可以用于求偏导数
求下列函数的导数:
(1) y = 1 + e x y=\sqrt{1+e^x} y=1+ex,求 y ′ y' y′
(2) z = x e y y 2 z=\frac{xe^y}{y^2} z=y2xey,求 z x ′ z'_x zx′, z y ′ z_y' zy′
syms x y;
f=sqrt(1+exp(x));
diff(f)
g=x*exp(y)/y^2;
diff(g,x)
diff(g,y)
结果如下:
ans =
exp(x)/(2*(exp(x) + 1)^(1/2))
ans =
exp(y)/y^2
ans =
(x*exp(y))/y^2 - (2*x*exp(y))/y^3
符号函数的积分
极限、导数、微分的概念是紧密关联的。有极限是可导的前提,而导数是微分之商,因此导数也称为微商。
**不定积分:**在MATLAB中,求不定积分的函数是int,其常用的调用格式为:int(f,x),即求函数f对变量x的不定积分。
**定积分:**在MATLAB中,定积分的计算也使用int命令,但调用格式有区别:int(f,x,a,b)。其中,a、b分别表示定积分的下限和上限。
- 当函数f关于变量x在闭区间[a,b]可积时,函数返回一个定积分结果。
- 当a、b中有一个是inf时,数返回一个广义积分。
- 当a、b中有一个符号表达式时,函数返回一个符号函数。
求下列不定积分:
(1)$\int (3-x2)3,dx $
(2)$\int \frac{5xt}{1+x^2},dt $
syms x t;
f=(3-x^2)^3;
int(f)
g=5*x*t/(1+x^2);
int(g,t)
结果如下:
ans =
- x^7/7 + (9*x^5)/5 - 9*x^3 + 27*x
ans =
(5*t^2*x)/(2*(x^2 + 1))
求下列定积分:
(1)$\int_1^2 |1-x|,dx $
(2)$\int_{-\infty}^{+\infty} \frac{1}{1+x^2},dx $
(3)$\int_2^{sinx} \frac{4x}{t},dt $
syms x t;
int(abs(1-x), 1, 2)
int(1/(1+x^2), -inf, inf)
int(4*x/t, t, 2, sin(x))
结果如下:
ans =
1/2
ans =
pi
ans =
4*x*(log(sin(x)) - log(2))
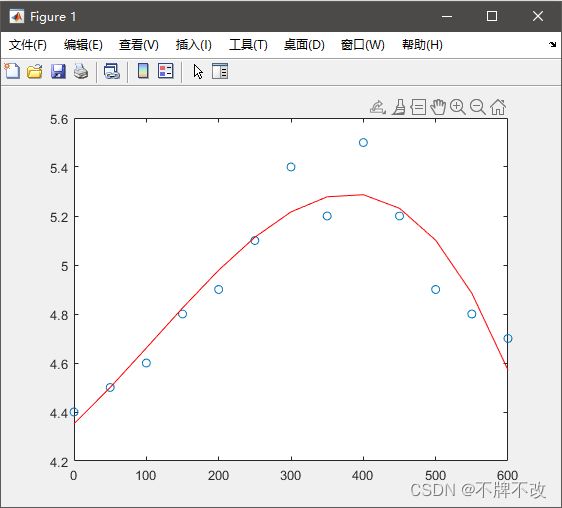
河道水流的估计问题:
根据实际测量,得到河流某处宽600m,其横截面不同位置某一时刻的水深如下表所示:
| x | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 600 |
| h(x) | 4.4 | 4.5 | 4.6 | 4.8 | 4.9 | 5.1 | 5.4 | 5.2 | 5.5 | 5.2 | 4.9 | 4.8 | 4.7 |
(表格中数据的意思是取某个与水流方向垂直的截面作为研究对象,对这个截面位置的水深进行调查如上表)
(1)若此刻水流的流速为0.6m/s,试估计该河流此刻的流量。
(2)已知x方向[50,60]区间为坡式护岸的下部护脚部分,根据相关堤防设计规范,抛石护岸护脚坡度应缓于1:1.5(正切值),请估计水流冲刷是否已破坏该区域的护脚。
分析:
(1)先拟合出河床曲线,然后进行定积分,计算出河流横截面,再利用流量与流速关系公式 Q = S v Q=Sv Q=Sv,即可估计流量。(也可以使用微元法计算曲线与坐标系围成的面积)
xi=0:50:600;
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7];
p=polyfit(xi,yi,3); % 拟合
plot(xi,yi,'o', xi,polyval(p,xi),'r'); % 绘图
syms y x;
y=poly2sym(p,x);% p是多项式系数向量,x是符号变量;此函数求得p作为多项式系数,x作为变量的多项式
s=int(y,x,0,600); % 计算横截面面积 % 对关于x的函数表达式y从0积分到600,返回积分值
v=s*0.6; % 计算水流量
eval(v) % v是符号表达式形式
结果如下:
ans =
1.7874e+03
水深曲线图如下:
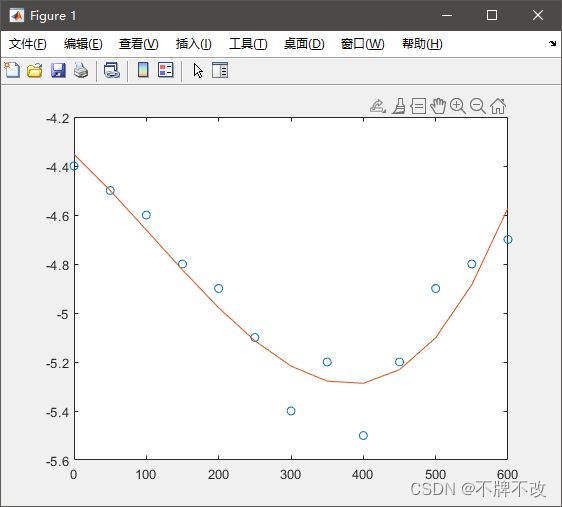
(2)根据河床曲线,计算其导函数,并判断相应范围内导函数的取值是否大于1:1.5。
视频中说要翻转曲线是因为题目中给的数据是“位置-水深”关系图,而第二问要计算河床曲线的导函数,由于水平面处处相等,水深的地方河床自然低,水浅的地方河床自然高,这就是为什么两条曲线是相反的原因。但其实对于判断“50~60的位置内是否大于1:1.5”没必要翻转,直接用上面的求斜率即可。(代码还是按视频老师讲解写的)
%% h
xi=0:50:600;
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7];
yn=-yi;
p=polyfit(xi,yn,3);
plot(xi,yn,'o',xi,polyval(p,xi));
%% 符号函数计算
syms y x yii;
y=poly2sym(p,x);
yii=diff(y,x); % 求得的就是导数,无需除以Δx
x=50:60; % x变化范围
k=eval(yii); % 当自变量x确定时,可以通过eval计算函数的值
all(abs(k)<1/1.5) % 逻辑值全为1,该函数返回逻辑值1,否则返回逻辑值0
%% 也可以用求数值导数的方法来做
x=50:60;
y=polyval(p,x);
k=diff(y)/1; % 此时的diff求得的是差分,而不是导数,因此需要除以Δx
all(abs(k)<1/1.5)
%% 用polyder函数求解
x=50:60;
p1=polyder(p); % 导函数的系数向量
k=polyval(p1, x);
all(abs(k)<1/1.5)
结果如下:
ans =
logical
1
ans =
logical
1
ans =
logical
1
河床曲线图如下:
all函数
matlab中all(x) 表示:
-
如果x是一个向量,则如果x的所有元素都不等于0,all(x)返回1,否则返回0.
-
如果x是一个矩阵,则沿着列的方向,判断x的每一列是否包含0元素。对于各列,如果不包含0元素,则返回1否则0。这样all(x)最终得到一个行向量,每个元素是都x的每一列的判断结果。类似地,如果想判断x的每一行是否不包含0元素,使用all(x,2),表示沿着x的第二个维度即行的方向判断。
级数
级数求和
用sum求和的项数必须有限,而当项数非常多或无限时,sum无法解决。
求无穷级数的和需要符号表达式求和函数symsum(),其调用格式为:symsum(s,v,n,m)
其中,s表示一个级数的通项,是一个符号表达式。v是求和变量,v省略时使用系统的默认变量。n和m是求和变量v的初值和末值。
求下列级数之和:
(1) s 1 = 1 + 4 + 9 + 16 + … … + 10000 s_1=1+4+9+16+……+10000 s1=1+4+9+16+……+10000
(2) s 2 = 1 − 1 2 + 1 3 − 1 4 + … … + ( − 1 ) n + 1 1 n + … … s_2=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+……+(-1)^{n+1} \frac{1}{n}+…… s2=1−21+31−41+……+(−1)n+1n1+……
(3) s 3 = 1 − 1 3 + 1 5 − 1 7 + … … + ( − 1 ) n + 1 1 2 n − 1 + … … s_3=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+……+(-1)^{n+1} \frac{1}{2n-1}+…… s3=1−31+51−71+……+(−1)n+12n−11+……
syms n;
s1=symsum(n^2,1,100) % 338350
s2=symsum((-1)^(n-1)/n,1 ,inf) % log(2)
s3=symsum((-1)^(n-1)/(2*n-1),n,1 ,inf) % hypergeom([-1/2, 1], 1/2, -1) - 1
hypergeom([-1/2,1],1/2,-1) % 1.7854
eval(s3)*4 % 3.1416 % pi
假设某人在银行存款50000元,年利率为4.5%,按复利计息(即下一年利息的计算要将这一年得到的利息算入本金)。
(1)若半年期计息一次,请问一年后总金额是多少?
(2)若每季度计息一次,请问一年后总金额是多少?
(3)若每月计息一次,请问一年后总金额是多少?
(4)若计息时间无限短,即计息期数趋于无穷,则一年后总金额是多少?
问题分析:
假设存款(初始总金额)为 p p p,年利率为 r r r,计息期数为 k k k。第一期后总金额为 p ∗ ( 1 + r / k ) p*(1+r/k) p∗(1+r/k)。
第二期后总金额为 p ∗ ( 1 + r / k ) 2 p*(1+r/k)^2 p∗(1+r/k)2。
第三期后总金额为 p ∗ ( 1 + r / k ) 3 p*(1+r/k)^3 p∗(1+r/k)3。
依此类推,第k期后总金额为 p ∗ ( 1 + r / k ) k p*(1+r/k)^k p∗(1+r/k)k。
syms k r;
p2=symsum(50000*(1+0.045/k)^k,k,2,2);
eval(p2) % 5.2275e+04
p4=symsum(5000*(1+0.045/k)^k,k,4,4);
eval(p4) % 5.2288e+03
p12=symsum(50000*(1+0.045/k)^k,k,12,12);
eval(p12) % 5.2297e+04
limit((1+r/k)^k,k, inf) % exp(r)
50000*exp(0.045) % 5.2301e+04
所以,即使是无数次计息,只要年利率确定,总金额也不会无限增长,它收敛于 p e r pe^r per。
注意:在级数的计算中,因为小数都表示为有理分数的形式,容易导致分子或分母出现极大整数从而无法计算的情况。
泰勒级数
MATLAB提供了taylor()函数将函数展开为幂级数。其调用格式为:taylor(f,v,a,Name,Value)
该函数将函数f按变量v在a点展开为泰勒级数,v省略时按默认规则确定变量,a的默认值是0。Name和Value为选项设置,经常成对使用,前者为选项名,后者为该选项的值。
Name有3个取值:
- ‘ExpansionPoint’:指定展开点,对应值可以是标量或向量。未设置时,展开点为0。
- ‘Order’:指定截断参数,对应值为一个正整数。未设置时,截断参数为6,即展开式的最高阶为5。
- ‘OrderMode’:指定展开式采用绝对阶或相对阶,对应值为’Absolute’或’Relative’。未设置时取’Absolute’。
求函数f在x=1处的5阶泰勒级数展开式:
f ( x ) = 1 + x + x 2 1 − x + x 2 f(x)=\frac{1+x+x^2}{1-x+x^2} f(x)=1−x+x21+x+x2
syms x;
f=(1+x+x^2)/(1-x+x^2);
taylor(f,x,1 ,'Order',6) % 2*(x - 1)^3 - 2*(x - 1)^2 - 2*(x - 1)^5 + 3
expand(ans) % - 2*x^5 + 10*x^4 - 18*x^3 + 12*x^2 + 1 % 调用符号表达式展开函数,将其展开成多项式的形式
cos、sin等函数不像四则运算一样直接通过底层的逻辑电路实现,这些函数需要先用泰勒展式将其展开后再进行四则运算计算得到
符号方程求解
代数方程符号求解
在MATLAB中,求解用符号表达式表示的代数方程可由函数solve( )实现,其调用格式为:
- solve(s):求解符号表达式s的代数方程,求解变量为默认变量。
- solvels,v):求解符号表达式s的代数方程,求解变量为v。
- solve(s1,s2,… ,sn,v1,v2,…,vn):求解符号表达式s1,s2, …, sn组成的代数方程组,求解变量分别为v1,v2,…, vn。
解方程 a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0:
syms x y a b c;
%%
solve(a*x^2+b*x+c==0)
f-a*x^2+b*x+c==0;
solve(f)
%% 当等式的全部项都移至等式左侧,等式右侧为0时,可以直接将a*x^2+b*x+c作为参数
solve(a*x^2+b*x+c)
f=a*x^2+b*x+c;
solve(f)
% 四个输出均如下
ans =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a)
-(b - (b^2 - 4*a*c)^(1/2))/(2*a)
注意:在运用solve函数进行方程求解时所得到的结果不一定准确,有的方程或方程组明明有解,MATLAB却给出无解的答案。在进行解方程的时候,还需要用多种方法进行试探求解。
常微分方程符号求解
在MATLAB中,用大写字母D表示导数。
例如:
Dy表示y’,D2y表示y",Dy(0)=5表示y’(0)=5。
D3y+D2y+Dy-x+5=0表示微分方程y"“+y”+y’-x+5=0。
符号常微分方程求解可以通过函数dsolve来实现,其调用格式为:dsolve(e,c,v)
用于求解常微分方程e在初值条件c下的特解。参数v是方程中的自变量,省略时按默认原则处理,若没有给出初值条件c,则求方程的通解。
dsolve在求常微分方程组时的调用格式为:dsolve(el,e2,…,en,c1,c2,…,cn,v)
用于求解常微分方程组e1,e2,…, en在初值条件c1,c2,…, cn下的特解,若不给出初值条件,则求方程组的通解。v给出求解变量,如果没有指定自变量,则采用默认自变量t。
求下列常微分方程或方程组的解:
(1) d y d x = x 2 + y 2 2 x 2 \frac{dy}{dx} = \frac{x^2+y^2}{2x^2} dxdy=2x2x2+y2
(2)Cannot read properties of undefined (reading 'type')
syms x y t;
y=dsolve('Dy-(x^2+y^2)/x^2/2',x)
[x,y]=dsolve('Dx=4*x-2*y','Dy=2*x-y',t)
结果如下:
y =
-x*(1/(C1 + log(x)/2) - 1)
x
x =
C1/2 + 2*C2*exp(3*t)
y =
C1 + C2*exp(3*t)
其中的Ci表示的是待定系数;
执行上面的程序会出现警告:“Support of character vectors and strings will be removed in a future release. Use sym objects to define differential equationsinstead.”,经百度,是因为此用法是老版本。
疾病传染问题
通过传染病模型来描述传染病的传染过程,分析受感染人数的变化规律,预报传染病高潮的到来等,一直是研究人员所关注的课题。以下是一个传染病模型:
假设条件:
- 人群分为易感者和已感者两类,在时刻t这两类人在总人数中所占的比例分别为 s ( t ) s(t) s(t)和 y ( t ) y(t) y(t)。
- 每个病人每天有效接触的平均人数是常数 λ \lambda λ, λ \lambda λ称为日接触率。当病人与健康者有效接触时,健康者受感染成为病人。
- 病人每天被治愈的占病人总数的比例为 μ \mu μ,称为日治愈率,显然, 1 / μ 1/\mu 1/μ是这种传染病的平均传染期。
根据假设,每个患者每天可使 λ s ( t ) \lambda s(t) λs(t)个健康者变为病人,每天有比例为 μ \mu μ的病人被治愈。因为病人数为 N y ( t ) Ny(t) Ny(t)( N N N为总人数),故每天共有 ( s ( t ) N y ( t ) − μ N y ( t ) ) (s(t)Ny(t)- \mu Ny(t)) (s(t)Ny(t)−μNy(t))个健康者变为病人,即有:
N d y d t = λ N s y − μ N y N\frac{dy}{dt}=\lambda Nsy-\mu Ny Ndtdy=λNsy−μNy
又因为 s ( t ) + y ( t ) = 1 s(t)+y(t)=1 s(t)+y(t)=1,初始时刻 ( t = 0 ) (t=0) (t=0)病人比例 b b b为常数,则:
Cannot read properties of undefined (reading 'type')
syms a b c y t;
f=dsolve('Dy=a*y*(1-y)-c*y','y(O)=b',t)
% ((a - c)*(tanh((t + (2*atanh((2*a*b)/(a - c) - 1))/(a - c))*(a/2 - c/2))+ 1))/(2*a)
结果报错,不知道原因,视频结果为上面代码注释部分。
假如 λ = μ \lambda=\mu λ=μ,即 a = c a=c a=c,则再次解常微分方程得到结果为:1/(a*t + 1/b)
这时得到一个非常简洁的结果,即 y ( t ) = b λ b t + 1 y(t)=\frac{b}{\lambda bt+1} y(t)=λbt+1b
结论:
当 λ ≤ μ \lambda≤\mu λ≤μ时,病人比例 y ( t ) y(t) y(t)越来越小,最终趋于0。
当 λ > μ \lambda>\mu λ>μ时, y ( t ) y(t) y(t)的增减值取决于 b b b的大小,并随着 t t t趋于无穷大,最终存在极限。
y ( ∞ ) = 1 − μ λ y(\infty)=1-\frac{\mu}{\lambda} y(∞)=1−λμ