一万字彻底学会栈和队列
本文章是对栈和队列的详细总结，包含顺序表和链表存储数据的优缺点，栈和队列的接口实现，栈和队列的相互模拟实现，以及循环队列的实现
栈和队列
- 栈
-
- 一、栈的基本介绍
- 二、栈的结构选择
-
- ⭐⭐⭐顺序表和链表的优缺点
- 三、栈的接口实现
-
- 1、栈的构造
- 2、栈的接口预览
- ①栈的初始化
- ②栈的销毁
- ③入栈
-
- 扩容
- ④出栈
- ⑤获取栈顶数据
- ⑥判断是否为空
- ⑦求栈的大小
- 队列
-
- 一、队列的基本介绍
- 二、队列的结构选择
- 三、队列的接口实现
-
- 1、队列的构造
- 2、队列的接口预览
- ①队列的初始化
- ②队列的销毁
- ③入队
- ④出队
- ⑤取出队头数据
- ⑥取出队尾数据
- ⑦判断是否为空
- ⑧求队列的大小
- 1️⃣用队列实现栈
- 2️⃣用栈实现队列
- 3️⃣设计循环队列
栈
一、栈的基本介绍
栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
可以把栈理解为弹匣，进出子弹的地方叫栈顶，另一端叫栈底，进子弹就叫压栈，出子弹就叫出栈，不管是出栈还是进栈，都只能从栈顶进出。
二、栈的结构选择
因为栈和线性表相似，所有有两种存储方式：1️⃣顺序栈 2️⃣链栈
要选择结构我们可以用图来分析
当要出数据时，用顺序栈只需要将top（栈顶）大小减 1 就行
而链栈则需要遍历链表找到尾指针，而且需要两个指针。
当要入数据时，顺序栈只需要将top加 1 就行
而链栈则需要找尾再加数据。
综上考虑，顺序栈更为合适。
⭐⭐⭐顺序表和链表的优缺点
在很多地方都要选择顺序表或者链表来存储数据，那么我们就来总结一下他们的优缺点
顺序表的优点：
1、可以按照下标随机访问空间
2、cpu的高速缓存命中比较高（一整段的截取空间）
链表的优点：
1、需要空间就申请，不存在空间浪费，不存在性能消耗
2、如果知道插入位置，时间复杂度就是O(1)
顺序表缺点：
1、空间不够扩容一般扩容两倍，势必存在空间浪费
2、当插入数据时候要挪动其他数据，时间复杂度O(N)
链表缺点
1、不支持随机访问(要遍历找到尾)
2、cpu高速缓存命中率低
三、栈的接口实现
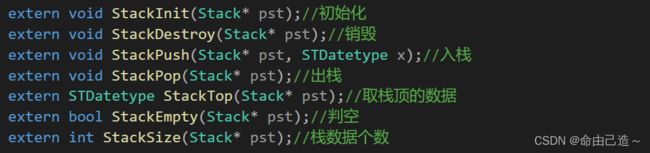
1、栈的构造
2、栈的接口预览
①栈的初始化
初始化就可以先开辟一定的空间，因为如果空间不够的时候可以直接realloc两倍的空间。
void StackInit(Stack* pst)
{
assert(pst);
//初始化先开辟四个整形的空间
pst->a = (STDatetype*)malloc(sizeof(STDatetype) * 4);
pst->capacity = 4;
pst->top = 0;
}
②栈的销毁
因为a就是指向数组的指针，把a的空间释放掉就是把数组销毁了
void StackDestroy(Stack* pst)
{
assert(pst);
free(pst->a);
pst->capacity = pst->top = 0;
pst->a = NULL;
}
③入栈
我们直到入栈要考虑数组的空间是否足够，为了让接口的工作单一，我们可以写一个扩容函数：
扩容
void StackCheck(Stack* pst)
{
assert(pst);
//判断是否满了
if (pst->capacity == pst->top)
{
STDatetype* p = (STDatetype*)realloc(pst->a,
sizeof(STDatetype) * 2 * (pst->capacity));
if (p == NULL)
{
printf("realloc fail\n");
exit(-1);
}
else
{
pst->a = p;
pst->capacity *= 2;
}
}
}
入栈
void StackPush(Stack* pst, STDatetype x)
{
assert(pst);
//判断是否满了
StackCheck(pst);
pst->a[pst->top] = x;
pst->top++;
}
④出栈
先要判断是否为空
void StackPop(Stack* pst)
{
assert(pst);
assert(!StackEmpty(pst));
pst->top--;
}
⑤获取栈顶数据
先要判断是否为空
STDatetype StackTop(Stack* pst)
{
assert(pst);
assert(!StackEmpty(pst));
return pst->a[pst->top - 1];
}
⑥判断是否为空
bool StackEmpty(Stack* pst)
{
return pst->top == 0;
}
⑦求栈的大小
int StackSize(Stack* pst)
{
return pst->top + 1;
}
以上就是栈的基本操作，下面就进入队列的学习啦
队列
一、队列的基本介绍
队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。
二、队列的结构选择
如果我们要用顺序表来存储，我们知道取出一个元素要从队头取，也就是数组的第一个元素，这样势必会挪动数据，那样时间复杂度就很高了。
如果用链表，那么出队列直接就是头删，很方便，所以我们选择链表。
三、队列的接口实现
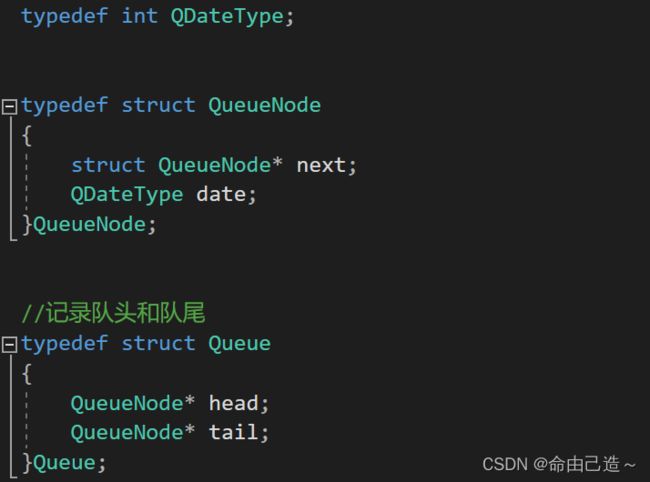
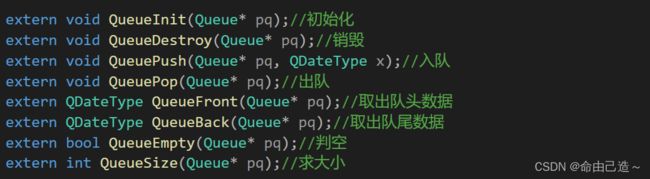
1、队列的构造
2、队列的接口预览
①队列的初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
}
②队列的销毁
队列的销毁比栈要麻烦，因为链表需要一个结点一个结点的销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
while (cur)
{
QueueNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
③入队
入队就是创造一个结点连在tail的后面，也要注意链表为空的情况
void QueuePush(Queue* pq, QDateType x)
{
assert(pq);
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
newnode->date = x;
newnode->next = NULL;
if (pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
}
④出队
要注意两点
1️⃣队列不能为空
2️⃣只有一个结点特殊处理
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
//只有一个结点
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
}
⑤取出队头数据
QDateType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->date;
}
⑥取出队尾数据
QDateType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->date;
}
⑦判断是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL;
}
⑧求队列的大小
int QueueSize(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
int count = 0;
while(cur)
{
cur = cur->next;
count++;
}
return count;
}
以上就是栈的基本操作，既然学完了栈和队列，那么我们就来让他们相互实现一下！！
1️⃣用队列实现栈
先来说说怎么把两个队列看成一个栈
为了方便表示，用两个正方形表示两个队列的空间，里面还是用链表实现的
① 当要入数据的时候找一个不为空的入（如果两个都为空就随便入一个）
②当要出数据的时候，留一个数在不为空的队列，剩下的移动到为空的队列
再把剩下的一个数据出队列。
以上操作刚好满足栈的"先进后出"原则。接下来我们就一步步来实现
根据题目要求我们首先要有两个队列（假设我们自己实现的队列的声明和定义都拷贝了过来）
typedef struct {
Queue q1;
Queue q2;
} MyStack;
上面只是结构体的定义，还没有真正的创造两个队列
接下来就是创造自己的栈（两个队列）
MyStack* myStackCreate() {
Mystack st;
return &St;
}
这种写法是错误的，因为在这个函数创建的是临时变量，出了函数就会销毁，别的函数一用就是野指针
正确写法：
MyStack* myStackCreate() {
MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
下面是"入栈"
要注意的是往非空的地方入
void myStackPush(MyStack* obj, int x) {
assert(obj);
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1, x);
}
else
{
QueuePush(&obj->q2, x);
}
}
下面是"出栈"
我们始终保持这一个队列为空，把不为空的数据挪动到为空的队列。
可以用假设的方法来表示两个队列
int myStackPop(MyStack* obj) {
Queue* pempty = &obj->q1;
Queue* pnoempty = &obj->q2;
if(!QueueEmpty(&obj->q1))
{
pempty = &obj->q2;
pnoempty = &obj->q1;
}
while(QueueSize(pnoempty) > 1)
{
QueuePush(pempty, QueueFront(pnoempty));
QueuePop(pnoempty);
}
int tmp = QueueFront(pnoempty);
QueuePop(pnoempty);
return tmp;
}
下面是获取"栈顶"的数据
栈顶就是非空队列的队尾
int myStackTop(MyStack* obj) {
assert(obj);
if(!QueueEmpty(&obj->q1))
{
return obj->q1.tail->date;
//return QueueBack(&obj->q1);
}
else
{
return obj->q2.tail->date;
//return QueueBack(&obj->q2);
}
}
下面是判断栈是否为空
只要两个队列都为空就是空
bool myStackEmpty(MyStack* obj) {
return (QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2));
}
下面是销毁栈
不要忘记自己申请的结构体指针
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->q1);
QueueDestroy(&obj->q2);
free(obj);
}
2️⃣用栈实现队列
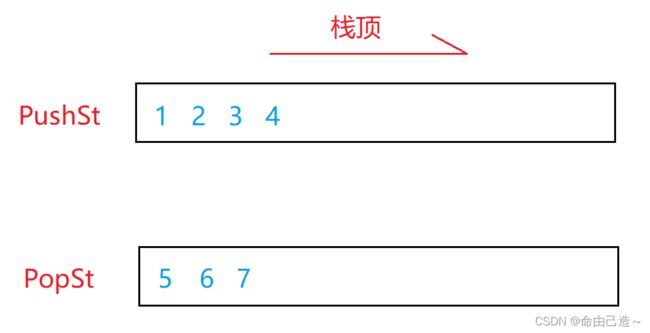
先来说说怎么把两个栈看成一个队列
①进数据的时候直接在PushSt进
而出数据的时候先要看PopSt是否为空
1、为空
把上面的全部按出栈的移动下来
2、不为空
先出下面的数据直到空
根据题目要求我们首先要有两个栈（假设我们自己实现的栈的声明和定义都拷贝了过来）
typedef struct {
Stack PushSt;
Stack PopSt;
} MyQueue;
上面只是结构体的定义，还没有真正的创造两个栈
接下来就是创造自己的队列（两个栈）
MyQueue* myQueueCreate() {
MyQueue* pst = (MyQueue*)malloc(sizeof(MyQueue));
StackInit(&pst->PushSt);
StackInit(&pst->PopSt);
return pst;
}
下面是将元素 x 推到队列的末尾
进队直接在PushSt进
void myQueuePush(MyQueue* obj, int x) {
StackPush(&obj->PushSt, x);
}
下面是从队列的开头移除并返回元素
出队的时候先要把PopSt的数据出完才行
int myQueuePop(MyQueue* obj) {
if(StackEmpty(&obj->PopSt))
{
while(!StackEmpty(&obj->PushSt))
{
StackPush(&obj->PopSt, StackTop(&obj->PushSt));
StackPop(&obj->PushSt);
}
}
int tmp = StackTop(&obj->PopSt);
StackPop(&obj->PopSt);
return tmp;
}
下面是返回队列开头的元素
int myQueuePeek(MyQueue* obj) {
if(StackEmpty(&obj->PopSt))
{
while(!StackEmpty(&obj->PushSt))
{
StackPush(&obj->PopSt, StackTop(&obj->PushSt));
StackPop(&obj->PushSt);
}
}
return StackTop(&obj->PopSt);
}
下面是判断队列是否为空
bool myQueueEmpty(MyQueue* obj) {
return StackEmpty(&obj->PushSt) && StackEmpty(&obj->PopSt);
}
下面是释放空间
void myQueueFree(MyQueue* obj) {
StackDestroy(&obj->PushSt);
StackDestroy(&obj->PopSt);
free(obj);
}
3️⃣设计循环队列
先来看一下逻辑结构方便理解
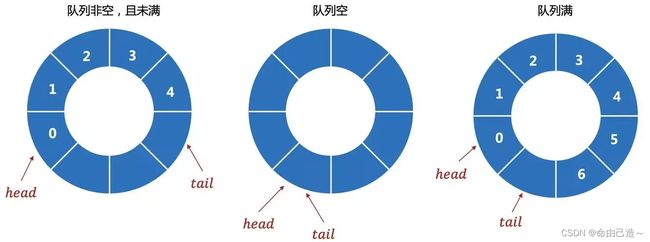
那么逻辑结构我们可以选择链表或者数组，由于大小是恒定的，我们选择数组也会方便些
物理结构如下
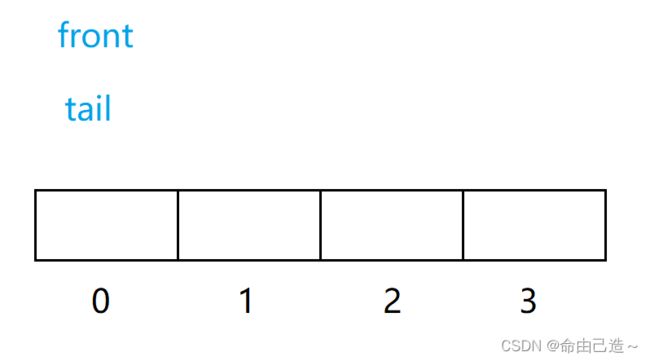
创造一个四个空间的数组，如果tail到了下标为3的位置，那么接下来就让它指向下标为0的空间，这样就形成了循环。
但是这里有一个问题是无法判断空和满（都是front == tail），解决办法是空出一个空间，当tail指向下标为3的空间时，就不能在入数据了，始终空出一个空间（任意位置）。这样tail的下一个空间是front的时候就满了。
本质上我们还是要建立个数组
typedef struct {
int* a;
int k;
int front;
int tail;
} MyCircularQueue;
k代表要需要开辟的空间
接下来就是创建结构体变量并初始化
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
cq->a = (int*)malloc(sizeof(int) * (k + 1));
cq->front = cq->tail = 0;
cq->k = k;
return cq;
}
要注意的是申请k + 1大小的空间。
下面是判断空满
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front == obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
int tailNext = obj->tail + 1;
if(tailNext == obj->k + 1)
{
tailNext = 0;
}
return tailNext == obj->front;
}
下面是向循环队列插入一个元素。如果成功插入则返回真
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->tail] = value;
obj->tail++;
if(obj->tail == obj->k + 1)
{
obj->tail = 0;
}
return true;
}
下面是从循环队列中删除一个元素。如果成功删除则返回真
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
obj->front++;
if(obj->front == obj->k + 1)
{
obj->front = 0;
}
return true;
}
下面是从队首获取元素。如果队列为空，返回 -1
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->a[obj->front];
}
下面是获取队尾元素。如果队列为空，返回 -1
这里注意要画图来避免踩坑
假设是这种情况
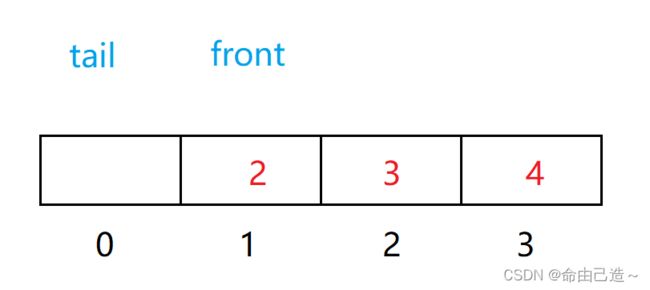队尾元素是4，如果要返回obj->a[obj->tail - 1]就会造成数组越界，所以要特殊处理
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
int tailprev = obj->tail - 1;
if(tailprev == -1)
{
tailprev = obj->k;
}
return obj->a[tailprev];
}
最后也别忘了释放空间
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
}