树形dp入门

目录

1.树形dp的定义
2.最大独立集
3. 树上背包
4. 树的最小顶点覆盖
5. 树的最长路径

1.树形dp的定义

树形dp是一种dp思想，将dp建立在树状结构的基础上。它是先算子树然后进行合并，即：先遍历子树，遍历完之后把子树的值合并给父亲。
树形dp的关键方法是dfs。从根节点出发，向子节点做深度优先搜索，并由其子节点的最优解合并得到该节点的最优解。

2.最大独立集

2.1 最大独立集的定义
独立集是指图 G 中两两互不相邻的顶点构成的集合。最大独立集是具有最大尺寸的独立集。
2.2例题
没有上司的舞会
题目链接AcWing算法基础课 285.没有上司的舞会

2.3思路
本道题是有向图，由上司指向职员。用动态数组去存储图的边。has_fa[i]表示i是否有父节点，1为有，0为没有。
构造两个状态0,1。f[i][0]表示不选择i点时，i点及其子树能得到的最大快乐指数。f[i][1]表示选择i点时，i点及其子树能得到的最大快乐指数。j为i的儿子节点，happy[i]表示i的幸运值。
f[i][0]=∑(max(f[j][0],f[j][1]))
f[i][1]=happy[i]+∑f[j][0]
结果为max(f[root][0],f[root][1])
2.4代码

//AC代码
#include
using namespace std;
#define int long long
const int N=6010;
int n,happy[N],has_fa[N],f[N][2];
vector<int> e[N];
void dfs(int u)
{
    f[u][1]=happy[u];
    for(int i=0;i<e[u].size();i++)
    {
        int j=e[u][i];
        dfs(j);
        f[u][1]+=f[j][0];
        f[u][0]+=max(f[j][0],f[j][1]);
    }
}
signed main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>happy[i];
    int m=n-1;
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        e[b].push_back(a);
        has_fa[a]=1;
    }
    int root=1;
    while(has_fa[root]) root++;
    dfs(root);
    cout<<max(f[root][1],f[root][0]);
    return 0;
}

3.树上背包

3.1 例题
有依赖的背包问题
题目链接AcWing算法提高课10.有依赖的背包问题
（算法提高课背包问题板块中）


3.2有依赖背包的定义
有依赖的背包问题是指物品之间存在依赖关系，这种依赖关系可以用一棵树来表示，要是我们想要选择子节点就必须连同其父节点一块选。
3.3思路
f[x][v]表达选择以x为子树的物品，在容量不超过v时所获得的最大价值。把有依赖的背包问题看成是分组背包问题，每一个结点是看成是分组背包问题中的一个组，子节点的每一种选择我们都看作是组内的一种物品，因此我们可以通过分组背包的思想去写。
3.4代码

//AC代码
#include
using namespace std;
const int N=110;
int n,m,f[N][N],v[N],w[N],root,x,y,z;
vector<int> e[N];
void dfs(int u)
{
    for(int i=0;i<(int)e[u].size();i++)//对当前结点的边进行遍历 
    {
        int son=e[u][i];
        dfs(son);
        for(int j=m-v[u];j>=0;j--){ 
        //遍历背包的容积，因为我们是要遍历其子节点，所以当前节点我们是默认选择的。
        //这个时候当前结点我们看成是分组背包中的一个组，子节点的每一种选择我们都看作是组内一种物品，所以是从大到小遍历。
        //我们每一次都默认选择当前结点，因为到最后根节点是必选的。 
            for(int k=0;k<=j;k++)
                f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
        }
    }
    for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];//加上刚默认选择的父节点价值
    for(int i=0;i<v[u];i++) f[u][i]=0;//去遍历子节点的组合 
}
signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>v[i]>>w[i]>>z;
        if(z==-1) root=i;
        else e[z].push_back(i);
    }
    dfs(root);
    cout<<f[root][m];
    return 0;
}

4.最小顶点覆盖

4.1例题
战略游戏
题目链接AcWing算法提高课——战略游戏

4.2思路
虽然是无向图，为了用树形dp，我们将其当作有向图处理，必须从根节点搜索。
f[i][1]以i为根的子树在i上放置的士兵的最少所需的士兵数目
f[i][0]以i为根的子树在i上不放置的士兵的最少所需的士兵数目
f[i][1]=1+∑min(f[j][0],f[j][1])
f[i][0]=∑f[j][j] (j是i的儿子)
结果为min(f[root][0],f[root][1])
4.3代码

#include
using namespace std;
#define int long long
vector<int>e[1510];
int t,n,x,y,st[1510],f[1510][2];
void dfs(int u)
{
    f[u][1]=1,f[u][0]=0;
    for(int i=0;i<(int)e[u].size();i++)
    {
        int j=e[u][i];
        dfs(j);
        f[u][0]+=f[j][1];
        f[u][1]+=min(f[j][1],f[j][0]);
    }
}
signed main()
{
    while(cin>>t)
    {
        memset(st,0,sizeof st);
        for(int i=0;i<t;i++) e[i].clear();
        while(t--)
        {
            cin>>n;
            
            scanf(":(%lld)",&x);
            while(x--)
            {
                cin>>y;
                e[n].push_back(y);
                st[y]=1;
            }
        }   
        int root=0;
        while(st[root]) root++;
        dfs(root);
        cout<<min(f[root][0],f[root][1])<<endl;
    }
    return 0;    
}

5.树的最长路径

5.1 例题
题目链接AcWing算法提高课 ——树的最长路径

5.2 思路
初始不确定树的拓扑结构，所以要建立双向边
先讨论对于给定拓扑结构的树里的任意节点，经过他的路径：

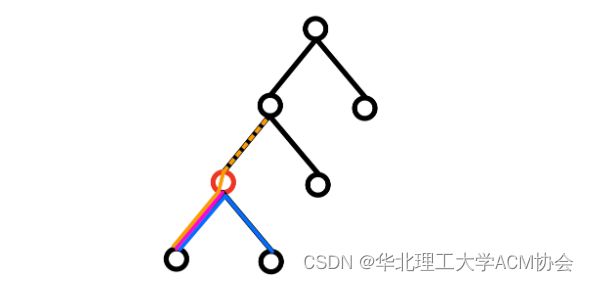
观察我标出的红色节点，那么经过他的路径有3种：
1.以其 子树中的某个节点 作为 起点，以他作为 终点 的 粉色路径
2.以其 子树中的某个节点 作为 起点，以子树中的某个节点作为终点的蓝色路径
3.以其 子树中的某个节点 作为 起点，以 非其子树的节点 作为 终点 的 橙色路径
对于第 1 种情况，我们可以直接递归处理其子树，找出到当前子树根节点最长的路径长度即可。
对于第 2 种情况，我们在处理第1 种情况时，顺便找出1类路径的 次长路径把最长和次长拼在一起，就是我们要的第 2 种情况。
而对于第 3 种情况，我们可以把它归类为其 祖先节点 的第 1,2种情况，让其 祖先节点 去处理即可。
d1表示以节点 u为根的子树中，从子树某个节点到 u 的最长路
d2表示以节点 u为根的子树中，从子树某个节点到 u 的次长路
ans为路径的最大长度。
5.3 代码

//AC代码
#include
#define int long long
using namespace std;
const int N=10010;
vector<pair<int,int>>s[N];
int ans,n,m,a,b,c;
int dfs(int u,int father)
{
    int dist=0;
    int d1=0,d2=0;
    for(int i=0;i<(int)s[u].size();i++)
    {
        auto j=s[u][i];
        if(j.first==father) continue;
        int d=dfs(j.first,u)+j.second;
        dist=max(dist,d);
        if(d>d1) d2=d1,d1=d;
        else if(d>d2) d2=d;
    }
    ans=max(ans,d1+d2);
    return dist;
}
signed main()
{
    cin>>n;
    n--;
    while(n--)
    {
        cin>>a>>b>>c;
        s[a].push_back({b,c});
        s[b].push_back({a,c});
    }
    dfs(1,-1);
    cout<<ans;
    return 0;
}