Python Leetcode回溯之排列、组合、子集问题
排列、组合、子集问题
1.给定的数组和要求存在以下情况:
(1)数组含重复元素,(2)数组不含重复元素;
(3)每个元素可多次使用,(4)每个元素只能使用一次;
一.排列
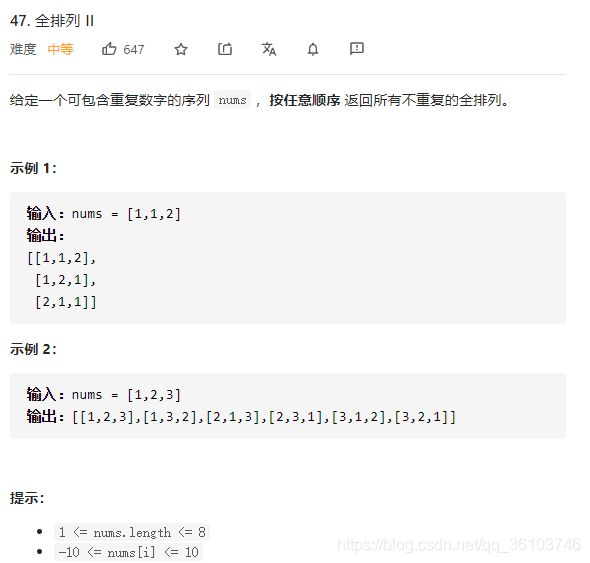
(1)全排列问题,需去重!
全排列2
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
nums.sort()
length = len(nums)
visit = [False for _ in range(length)]
res = []
self.backtrack(0, nums, res, [], visit)
return res
def backtrack(self, d, nums, res, temp, visit):
if d == len(nums):
res.append(temp)
return
for i in range(len(nums)):
if not visit[i]:
if i > 0 and nums[i] == nums[i - 1] and not visit[i - 1]:
continue
visit[i] = True
self.backtrack(d + 1, nums, res, temp + [nums[i]], visit)
visit[i] = False
(2)全排列问题,不存在重复答案。
全排列
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
length = len(nums)
res = []
visit = [False for _ in range(length)]
self.backtrack(0, nums, res, [], visit)
return res
def backtrack(self, d, nums, res, temp, visit):
if d == len(nums):
res.append(temp)
return
for i in range(len(nums)):
if not visit[i]:
visit[i] = True
self.backtrack(d + 1, nums, res, temp + [nums[i]], visit)
visit[i] = False
由以上两个题可以知道:排列问题需要设置一个visit数组,标记某个元素是否被使用;另外,如果数组含重复元素,需要进行剪枝以去重,即
if i > 0 and nums[i] == nums[i - 1] and not visit[i - 1]:
continue
二.组合
(2)+(3)组合总数
不含重复元素 + 元素可多次使用,且顺序无关
组合总和
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
candidates.sort()
self.dfs(candidates, target, [], res)
return res
def dfs(self, candidates, target, cur, res):
if target == 0:
res.append(cur) #[1, 2] + [3]语法产生了新的列表,一层一层传到根结点以后,直接res.append(cur). 注意与cur[:]的区别!!!
return
if target < candidates[0]: return
for i, num in enumerate(candidates):
self.dfs(candidates[i:], target - num, cur + [num], res)
(2) + (4)组合
不含重复元素 + 只能使用一次,且顺序无关。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if k > n: return []
res = []
self.backtrack(1, n, res, [], k)
return res
def backtrack(self, start, n, res, temp, k):
if len(temp) == k:
res.append(temp)
return
for i in range(start, n + 1):
self.backtrack(i+1, n, res, temp + [i], k)
# 剪枝!
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if k > n: return []
res = []
self.backtrack(1, n, res, [], k)
return res
def backtrack(self, start, n, res, temp, k):
if len(temp) == k:
res.append(temp)
return
# 例如7个元素中选择5个,则初始索引值最大只能达到7 - 5 + 1!
for i in range(start, n - (k - len(temp)) + 2):
self.backtrack(i+1, n, res, temp + [i], k)
(1) + (4) 组合总数2,需去重!
含重复元素+每个元素只能使用一次,且顺序无关
组合总数2
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
if not candidates: return []
if candidates[0] > target: return []
res = []
self.backtrack(0, target, res, [], candidates)
return res
def backtrack(self, start, target, res, temp, candidates):
if target == 0:
res.append(temp)
return
if target < candidates[0]: return
for i in range(start, len(candidates)):
if candidates[start] > target: break
if i > start and candidates[i] == candidates[i - 1]:
continue
self.backtrack(i + 1, target - candidates[i], res, temp + [candidates[i]], candidates)
由以上三题可知:组合数问题不需要设置visit数组,但需要设置搜索的起始索引值;组合与元素顺序无关,元素一样,顺序不一样仍属于同一个答案;同样,数组含重复元素需要进行去重,即:
if i > start and candidates[i] == candidates[i - 1]:
continue
三.子集
无重复元素
子集
# python列表迭代
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for i in nums:
res += [[i] + num for num in res]
return res
# 回溯
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
self.backtrack(nums, 0, [], res)
return res
def backtrack(self, nums, start, temp, res):
res.append(temp)
for i in range(start, len(nums)):
self.backtrack(nums, i + 1, temp + [nums[i]], res)
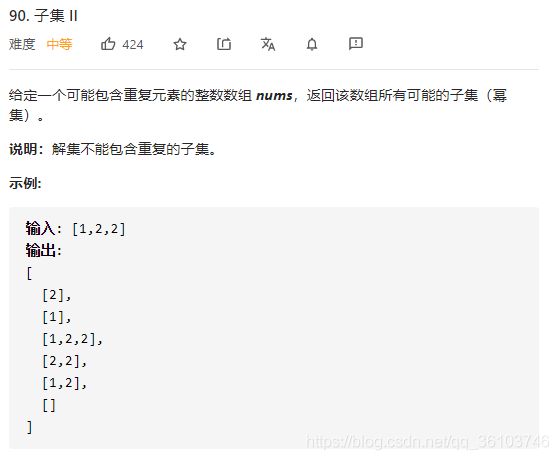
含重复元素
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
if not nums: return []
nums.sort()
res = []
self.backtrack(nums, 0, [], res)
return res
def backtrack(self, nums, start, temp, res):
res.append(temp)
for i in range(start, len(nums)):
if i > start and nums[i] == nums[i - 1]:
continue
self.backtrack(nums, i + 1, temp + [nums[i]], res)
由以上两题可知:子集问题也是需要设计搜索的起始索引值,不需要设计visit数组;同样,如果数组存在重复元素,也需要进行去重操作,即
if i > start and nums[i] == nums[i - 1]:
continue
四.总结
由以上几题,可总结:
- 该几类问题先进行数组排序(除不含重复元素的全排列问题和子集问题外);
- 全排列问题需要设置visit数组标记元素是否进行了搜索,组合问题和子集问题需要设置搜索的起始索引值;
- 数组含重复元素,需要进行剪枝,一般通过
if i > start and candidates[i] == candidates[i - 1]: continue进行去重处理。
排列序列

分析:
1.无重复元素,无需去重;2.排列问题,顺序有关,因此需要设计visit数组,记录元素是否搜索过;
因此代码可以写成如下:
class Solution:
def getPermutation(self, n: int, k: int) -> str:
res = []
visit = [False for _ in range(n + 1)]
self.backtrack(n, res, '', visit)
res.sort()
return str(res[k - 1])
def backtrack(self, n, res, temp, visit):
if len(temp) == n:
res.append(int(temp))
for i in range(1, n + 1):
if not visit[i]:
visit[i] = True
self.backtrack(n, res, temp + str(i), visit)
visit[i] = False
如上代码会超时,没有进行剪枝。由于只需要输出特定位的结果,因此可以对不满足的支进行剪枝。代码如下:
class Solution:
def getPermutation(self, n: int, k: int) -> str:
visit = [False for _ in range(n + 1)]
path = []
factorial = [1]
for i in range(1, n + 1):
factorial.append(factorial[-1] * i)
self.dfs(n, k, 0, path, factorial, visit)
return ''.join([str(num) for num in path])
# deep表示的是当前层,从0开始,最大的层即为n,表示搜索已经到了结点,此时得到一个搜索结果。
# 当前层为deep,则当前层每一个父节点可以产生的排列(结点)的个数为(n - 1 - deep)!
def dfs(self, n, k, deep, path, factorial, visit):
if deep == n: return
cnt = factorial[n - 1 - deep]
for i in range(1, n + 1):
if visit[i]:
continue
if cnt < k:
k -= cnt
continue
path.append(i)
visit[i] = True
self.dfs(n, k, deep + 1, path, factorial, visit)
# 直接加 return,后面的数没有必要遍历去尝试了
return