【CS224n】1斯坦福大学深度学习自然语言处理课程笔记
Natural Language Processing with Deep Learning 课程笔记1
- 一、 课程简介
- 二、Introduction and Word Vectors
-
- 1. The course
-
- 我们希望教什么?
- 作业计划
- 2. Human language and word meaning
-
- 同义词集WordNet
- 用离散的符号来表示单词
- 通过上下文来表示词语
- 3. Word2vec introduction
-
- 概述
- 目标函数
- Word2Vec与Vectors概述
- 4. Word2vec objective function gradients
-
- 梯度的Word2vec派生:
- More details
- 提高培训效率
- 5. Optimization basics
-
- 随机梯度下降
- 6. Looking at word vectors
- 小结
一、 课程简介
官网地址:CS224n: Natural Language Processing with Deep Learning
课程简介:Natural language processing (NLP) is a crucial part of artificial intelligence (AI), modeling how people share information. In recent years, deep learning approaches have obtained very high performance on many NLP tasks. In this course, students gain a thorough introduction to cutting-edge(尖端、先进) neural networks for NLP.
b站地址(1有字幕,2新一点没有字幕):
1、【官方】【中英】CS224n 斯坦福深度自然语言处理课 @雷锋字幕组
2、【英文字幕】2019最新版斯坦福大学 CS224n 深度学习自然语言处理
最新课程:Stanford / Winter 2021
二、Introduction and Word Vectors
The (really surprising!) result that word meaning can be represented rather well by a large vector of real numbers
1. The course
我们希望教什么?
-
1、深度学习的有效现代方法应用于NLP的基础——先讲基础知识,再讲NLP中使用的关键方法:循环网络、注意力、变换器等
-
2、对人类语言的全局认识,以及对人类语言的理解和产生的困难
-
3、了解并有能力为NLP中的一些主要问题建立系统(在PyTorch中):词义、依赖性解析、机器翻译、问题回答
作业计划
-
Ass1希望是一个简单的上坡–一个Jupyter/IPythonNotebook
-
Ass2是纯Python (numpy),但希望你能做(多变量)微积分,这样你才能真正理解基础知识
-
Ass3介绍了PyTorch,为依赖性解析构建一个前馈网络
-
Ass4和Ass5在GPU上使用PyTorch (Microsoft Azure) - 像PyTorch和Tensorflow这样的库现在是DL的标准工具
2. Human language and word meaning
GPT-3:通往普遍模式的第一步
Definition:meaning
- 由一个词、短语等代表的思想
- 一个人想通过使用文字、符号等表达的想法
- 在文字、艺术等作品中所表达的思想
最常见的语言学意义思维方式:
signifier能指(符号) ⟺signified所指(理念或事物)(指称语义学)
我们如何在计算机中拥有可用的意义?
常见的NLP解决方案:使用,例如:
同义词集WordNet
一个包含同义词集和超义词列表的词库("是一个 "关系)

WordNet等资源的问题:
- 作为资源很好,但缺少细微差别
- 例如,proficient"精通 "被列为 good"好 "的同义词,这只在某些情况下是正确的。
缺少新的词义 - 如:wicked, badass, nifty, wizard, genius, ninja, bombest ——邪恶的、坏蛋的、狡猾的、奇才的、天才的、忍者的、最厉害的等。
- 不可能保持更新!
- 主观
- 需要人力去创造和调整
- 无法计算出准确的单词相似度
用离散的符号来表示单词
在传统的NLP中,我们把单词看作是离散的符号:Hotel,Conference,Motel–一个局部主义的表示
这种文字的符号可以用one-hot(Means one 1, the rest 0s)向量来表示
motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
向量维度=词汇量的数量(如500,000)
问题:
例如:在网络搜索中,如果用户搜索 “Seattle motel”“西雅图汽车旅馆”,我们希望匹配包含 “Seattle hotel” "西雅图酒店 "的文档
但是:这两个向量是orthogonal正交的
对于one-hot 向量,没有similarity相似性的自然概念!
解决方法:是否可以尝试依赖WordNet的同义词列表来获得相似性?但众所周知会严重失败:不完整等。
取而代之的是:学会在向量本身中编码相似性
通过上下文来表示词语
- Distributional semantics分布式语义:一个词的意义是由经常出现在附近的词赋予的。现代统计学NLP最成功的思想之一!
- 当一个单词在文本中出现时,它的上下文是出现在附近的一组单词(在一个固定大小的窗口内)
- 利用w的多种语境来建立w的表象。

Word vectors单词向量
我们将为每一个词建立一个密集向量,选择使其与在类似上下文中出现的词的向量相似

注:词向量也叫词嵌入或(神经)词表示法 它们是一种分布式表示法
3. Word2vec introduction
概述
Word2vec(Mikolovet al. 2013)是一个学习词向量的框架思想:
- 我们有一个庞大的语料库(“主体”)文本
- 固定词汇中的每一个词都用一个向量来表示
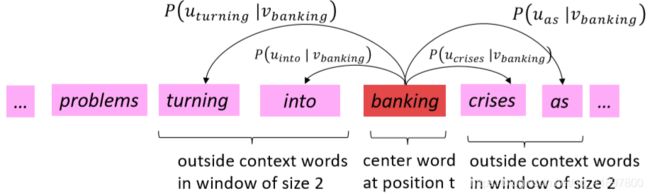
- 浏览文本中的每个位置t,其中有一个中心词c和上下文(“外部”)词o
- 利用c和o的词向量的相似性来计算给定c的概率(反之亦然)
- 不断调整词向量,使这个概率最大化
计算 P ( w t + j ∣ w t ) P\left(w_{t+j} \mid w_{t}\right) P(wt+j∣wt)的窗口和流程示例:
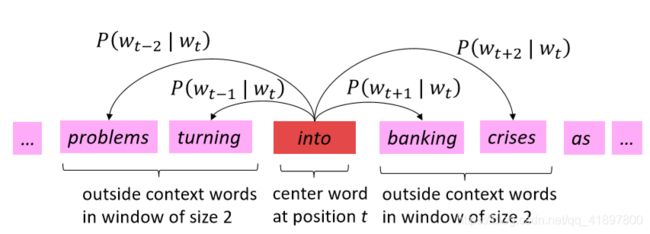
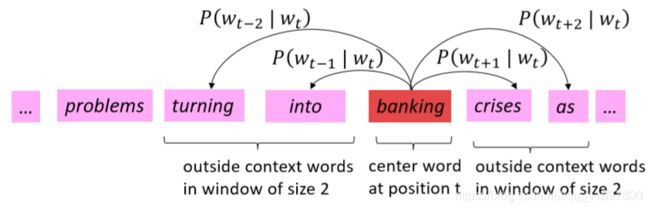
目标函数
对于每个位置 t = 1 , … , T t=1, \ldots, T t=1,…,T,在给定中心词 w j w_{j} wj的情况下,预测固定大小m的窗口中的上下文词。数据可能性:
L i k e l i h o o d = L ( θ ) = ∏ t = 1 T ∏ m ≤ j ≤ m j ≠ 0 P ( w t + j ∣ w t ; θ ) Likelihood =L(\theta)=\prod_{t=1}^{T} \prod_{m \leq j \leq m \atop j \neq 0} P\left(w_{t+j} \mid w_{t} ; \theta\right) Likelihood=L(θ)=t=1∏Tj=0m≤j≤m∏P(wt+j∣wt;θ)
是所有的变量都要优化
目标函数()是(平均)负对数似然率:
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} \mid w_{t} ; \theta\right) J(θ)=−T1logL(θ)=−T1t=1∑Tj=0−m≤j≤m∑logP(wt+j∣wt;θ)
最小化目标函数 ⟺最大化预测精度
我们要使以上目标函数最小化,
- 问题:怎么计算 P ( w t + j ∣ w t ; θ ) P\left(w_{t+j} \mid w_{t}; \theta\right) P(wt+j∣wt;θ)?
- 答案:我们将在每个单词w中使用两个向量:
当w是中心词时, v w v_{w} vw
当w是上下文词时, u w u_{w} uw
- 那么对于一个中心词c和一个上下文词o:
P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
Word2Vec与Vectors概述
P ( u problems ∣ v into ) P\left(u_{\text {problems }} \mid v_{\text {into }}\right) P(uproblems ∣vinto )是 P ( \mathrm{P}\left(\right. P( problems ∣ \mid ∣ into ; u problems , v into , θ ) \left.; u_{\text {problems }}, v_{\text {into }}, \theta\right) ;uproblems ,vinto ,θ)的简称
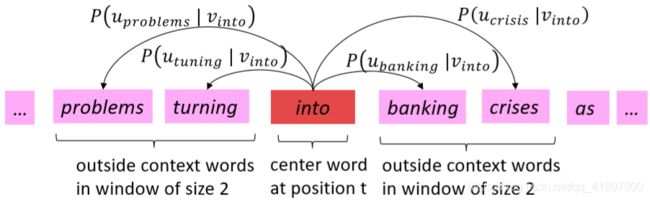
再来看预测函数:
P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
- u o T v c u_{o}^{T} v_{c} uoTvc——点积比较o和c的相似度, u T v = u . v = ∑ i = 1 n u i v i u^{T} v=u . v=\sum_{i=1}^{n} u_{i} v_{i} uTv=u.v=∑i=1nuivi,更大的点积表示更大的相似度
- 指数使任何东西变成正数
- 分母对整个词汇进行归一化处理,给出概率分布
这是softmax函数 R n → ( 0 , 1 ) n \mathbb{R}^{n} \rightarrow(0,1)^{n} Rn→(0,1)n(开放区域)的一个例子:
softmax ( x i ) = exp ( x i ) ∑ j = 1 n exp ( x j ) = p i \operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i} softmax(xi)=∑j=1nexp(xj)exp(xi)=pi
softmax函数将任意值 x i x_{i} xi映射到一个概率分布 p i p_{i} pi
- "max"是因为放大了最大 x i x_{i} xi的概率(但有点奇怪的名字,因为它返回的是一个分布)
- "soft"是因为仍然给较小的 x i x_{i} xi分配了一些概率
- 常用于深度学习
训练模型:优化参数值以减少损失
为了训练模型,我们逐步调整参数,使损失降到最低
- 回顾一下:代表所有的模型参数,在一个长的向量中
- 在我们的案例中,对于d维向量和V多字,我们有:
θ = [ v aardvark v a ⋮ v z e b r a u aardvark u a ⋮ u z e b r a ] ∈ R 2 d V \theta=\left[\begin{array}{l}v_{\text {aardvark }} \\ v_{a} \\ \vdots \\ v_{z e b r a} \\ u_{\text {aardvark }} \\ u_{a} \\ \vdots \\ u_{z e b r a}\end{array}\right] \in \mathbb{R}^{2 d V} θ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡vaardvark va⋮vzebrauaardvark ua⋮uzebra⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤∈R2dV - 记住:每个词都有两个向量
为什么是两个向量? 更容易优化,在最后平均两个向量 - 我们通过沿着梯度行走来优化这些参数
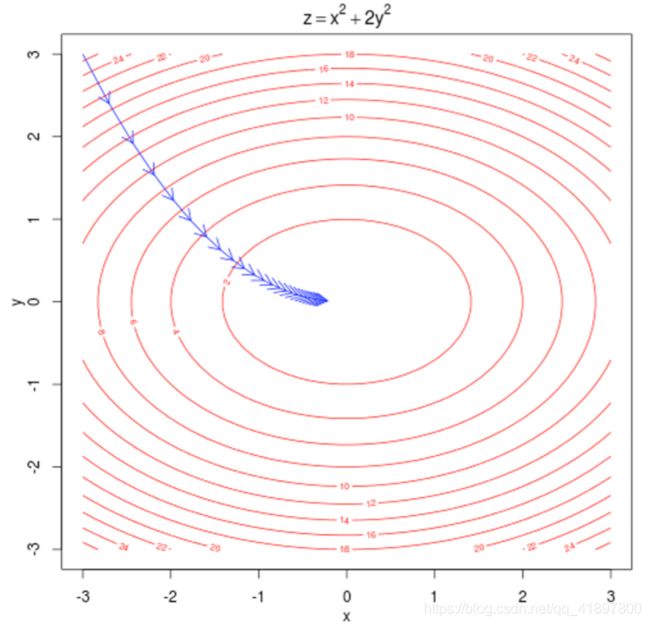
- 我们计算所有的向量梯度!
我们通过窗口中每个中心向量v的梯度
我们还需要外部向量u的梯度
一般来说,在每个窗口中,我们将计算更新该窗口中使用的所有参数。例如:
4. Word2vec objective function gradients
梯度的Word2vec派生:
- 链式法则
如果y=f(u),u=g(x),即y=f(g(x)),则:
d y d x = d y d u d u d x = d f ( u ) d u d g ( x ) d x \frac{d y}{d x}=\frac{d y}{d u} \frac{d u}{d x}=\frac{d f(u)}{d u} \frac{d g(x)}{d x} dxdy=dudydxdu=dudf(u)dxdg(x)
一个简单的例子: d y d x = d d x 5 ( x 3 + 7 ) 4 \frac{d y}{d x}=\frac{d}{d x} 5\left(x^{3}+7\right)^{4} dxdy=dxd5(x3+7)4
y = f ( u ) = 5 u 4 d y d u = 20 u 3 u = g ( x ) = x 3 + 7 d u d x = 3 x 2 d y d x = 20 ( x 3 + 7 ) 3 ⋅ 3 x 2 y=f(u)=5 u^{4}\\ \frac{d y}{d u}=20 u^{3} \\ \begin{aligned} u=g(x) &=x^{3}+7 \\ \frac{d u}{d x} &=3 x^{2} \end{aligned} \\ \frac{d y}{d x}=20\left(x^{3}+7\right)^{3} \cdot 3 x^{2} y=f(u)=5u4dudy=20u3u=g(x)dxdu=x3+7=3x2dxdy=20(x3+7)3⋅3x2 - 实用的基本事实: ∂ x T a ∂ x = ∂ a T x ∂ x = a \frac{\partial \mathbf{x}^{T} \mathbf{a}}{\partial \mathbf{x}}=\frac{\partial \mathbf{a}^{T} \mathbf{x}}{\partial \mathbf{x}}=\mathbf{a} ∂x∂xTa=∂x∂aTx=a
- 如有疑问:用指数写出来
More details
两种模型的变形:
- Skip-grams 跳格(SG) 给定中心词,预测上下文(“外部”)词(与位置无关)
- Continuous Bag of Words连续词袋(CBOW)从(词袋)语境词中预测中心词
本课至今:Skip-gram模型
提高培训效率
阴性取样
到目前为止:专注于 naïve softmax(更简单但更昂贵的训练方法)
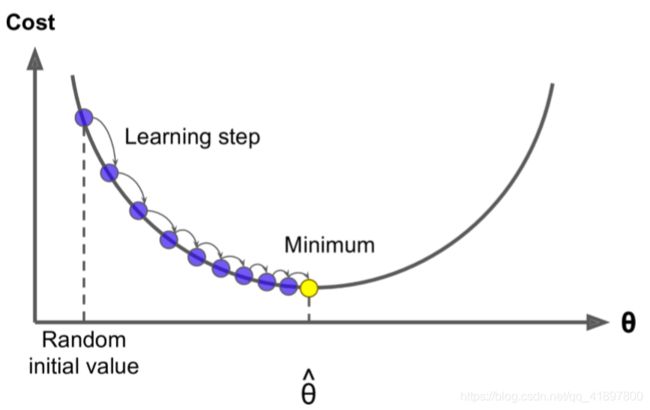
5. Optimization basics
- 我们有一个成本函数 (),我们想要最小化
- 梯度下降是一种最小化 ()的算法
更新方程(矩阵式):
θ new = θ old − α ∇ θ J ( θ ) \theta^{\text {new }}=\theta^{\text {old }}-\alpha \nabla_{\theta} J(\theta) θnew =θold −α∇θJ(θ)
=步长或学习率
更新方程(单参数):
θ j n e w = θ j o l d − α ∂ ∂ θ j o l d J ( θ ) \theta_{j}^{n e w}=\theta_{j}^{o l d}-\alpha \frac{\partial}{\partial \theta_{j}^{o l d}} J(\theta) θjnew=θjold−α∂θjold∂J(θ)
算法:
while True :
theta_ grad = evaluate_ gradient (J, corpus,theta)
theta = theta - alpha * theta grad
随机梯度下降
Stochastic Gradient Descent
- 问题:()是语料库中所有窗口的函数(可能是数十亿!)所以 ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)是非常昂贵的计算
- 你会等很久才进行一次更新!
- 对于几乎所有的神经网来说都是一个非常糟糕的想法!
- 解决办法:Stochastic gradient descent(SGD)——随机梯度下降(反复抽查窗口,每次抽查后都进行更新 )
- 算法:
while True:
window = s ample_ window ( corpus )
theta_ grad = evaluate_ gradient (J, window, theta)
theta = theta - alpha * theta_ grad
6. Looking at word vectors
小结
大致了解了自然语言处理概述、为什么选用Word2Vec模型,以及如何利用梯度下降进行计算