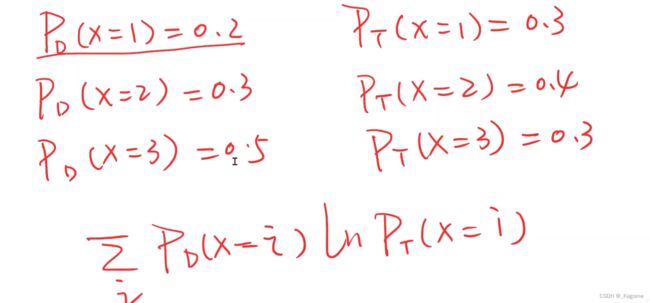Pytorch实践之Logistics Regression 逻辑回归

基本概念

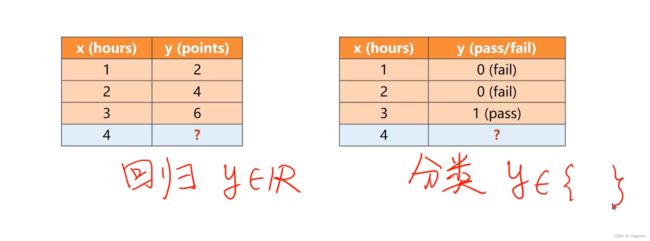
名字叫回归，但是是做分类的。

---

---

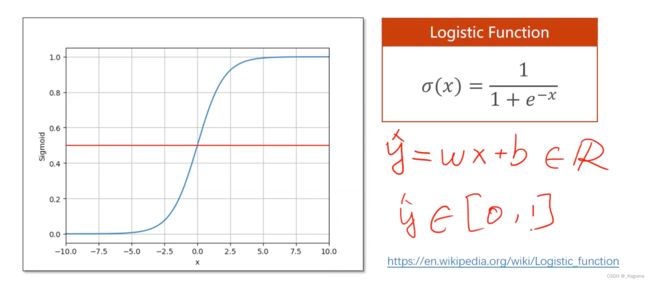
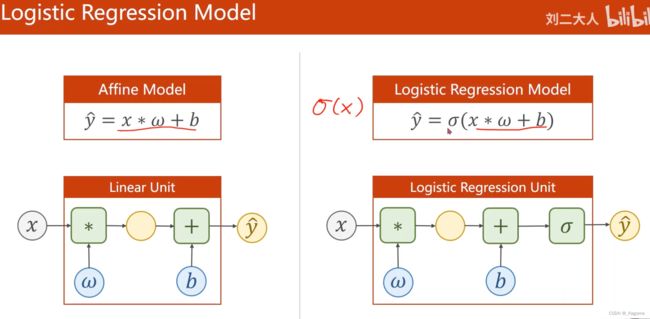
在logistics regression当中，其输出的是概率（因为做的是分类问题），所以范围是[0,1]，1/1+e^-x 是逻辑函数，其的作用就是将回归问题的输出映射到概率空间之内。x取值在(-∞,+∞)，使得y在(0,1)当中。

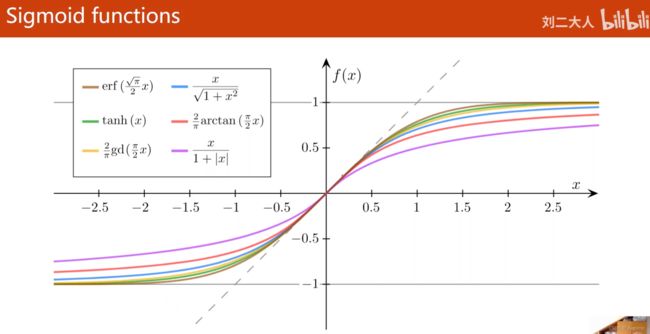
Sigmoid函数

饱和函数
范围固定

---

---

tanh(x) 双曲正切 常用 均值为0
[-1,1]
但是logistics function是输出0,1的，算是个SIGMOD的特殊函数

logistics function常常写成sigma(x)

加了一个负号代表越小越好

Loss是在数轴上计算两者的距离

注意这里比较的是两个分布之间的差异

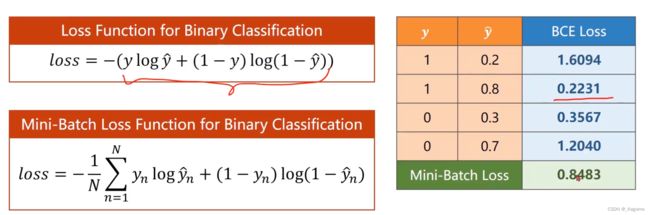
BCE Loss

是一个交叉熵的比较

损失函数的解释，总原则，loss趋于0是最好的

所以第一种y = 1，要让y_hat等于1，这样才能保证loss = 0
第二种同理

这函数叫做BCE Loss

计算损失常用的BCE函数
BCE损失当中的log其实是ln

sigma那边是没有参数的

关于BCELoss的详细解释：

参数说明

Weight：给每个batch元素的权重，一般没用
size_average: 默认为True
reduce: True/False 默认为True,对每个minibatch做
reduction: 用的比较多的是这个，若用了2.3可能导致4失效。

预测与标签越接近，BCE损失越小。

总结：二分类问题就用BCELoss，多分类的问题就用CrossEntropyLoss。

流程

现在都用BCE损失

代码：
编写网络模型都是这四步

与线性回归的变化

原来数据集是有各种各样的回归，现在变成了分类，就只有第0与第1类两个类别了（以二分类举例）

进行非线性的变换

优化器加入BCE损失
（BCELoss 是CrossEntropyLoss的一个特例，只用于二分类问题，而CrossEntropyLoss可以用于二分类，也可以用于多分类。如果是二分类问题，建议BCELoss ）

就是三个变化

进行测试

tips：view类似reshape

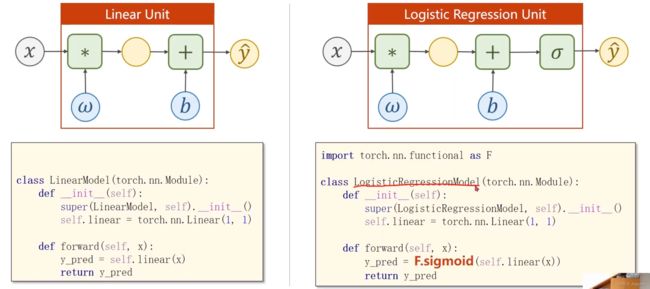
logistics regression说明：
1、 逻辑斯蒂回归和线性模型的明显区别是在线性模型的后面，添加了激活函数(非线性变换)
2、分布的差异：KL散度，cross-entropy交叉熵

代码实现

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import torch
import torchvision
#import torch.nn.functional as F
import matplotlib.pyplot as plt


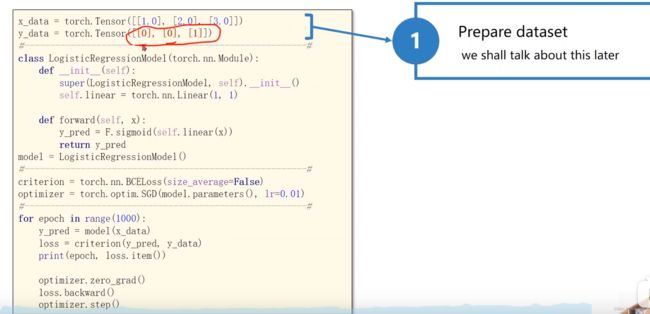
#第一步：准备数据集
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

epoch_list = []
loss_list = []

#第二步，设置模型，写成class的形式

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
       super(LogisticRegressionModel, self).__init__() #必须有的一句
       self.linear = torch.nn.Linear(1, 1) #定义所需要的权重与偏执，w与b
       
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x)) #视频中代码F.sigmoid(self.linear(x))会引发warning，此处更改为torch.sigmoid(self.linear(x))
        return y_pred

model = LogisticRegressionModel() #实例化

#第三步：设置损失函数以及优化器
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) #parameters是可以自动找出与权重匹配的值，lr是学习率

#第四步：训练循环，前馈，反馈，更新
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    epoch_list.append(epoch)
    loss_list.append(loss.item())
    print(epoch, loss.item())
    
    #以下三步就是更新步骤
    optimizer.zero_grad() 
    loss.backward()
    optimizer.step()
    
    
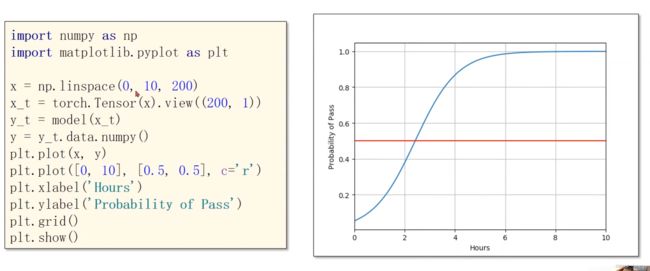
plt.xlabel('epoch')
plt.ylabel('loss')
plt.plot(epoch_list, loss_list)
plt.show()

回归与分类

分类问题：关键就是求解P(y_hat=1)的这个概率，从而进行判断是0还是1，从而进行分类。
回归问题：回归就是进行对图像进行拟合，通俗点就是降低loss，与分类问题表示完全不一样。

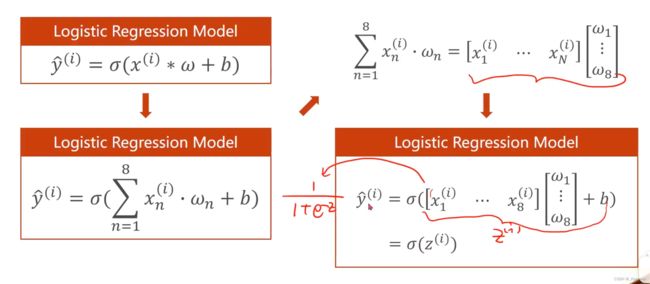
以下为多维度的分类
回归与分类的区别

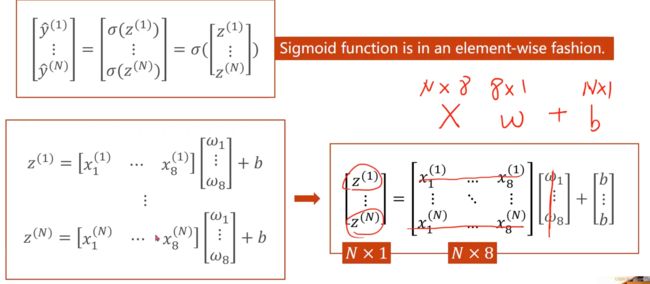
对这个向量运算的结果进行SIGMOD函数计算
pytorch提供的SIGMOD函数

是应用到每个元素上的向量函数

把向量的运算转换成矩阵的运算
可以利用并行计算的能力，来提高计算的速度

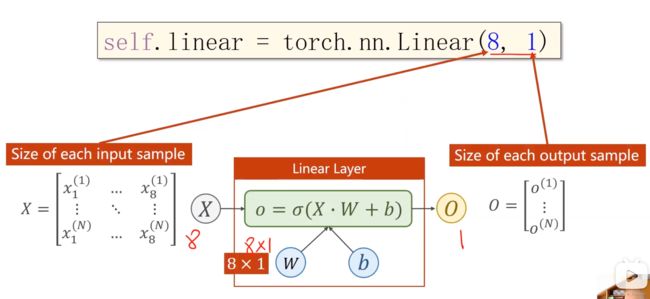
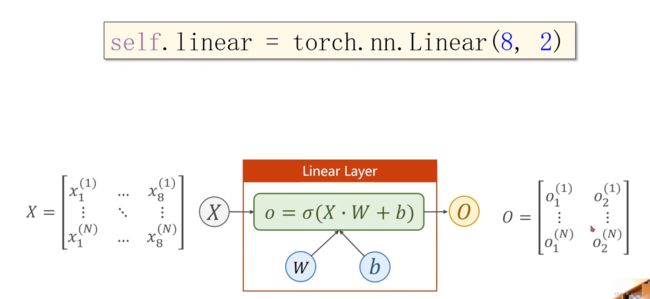
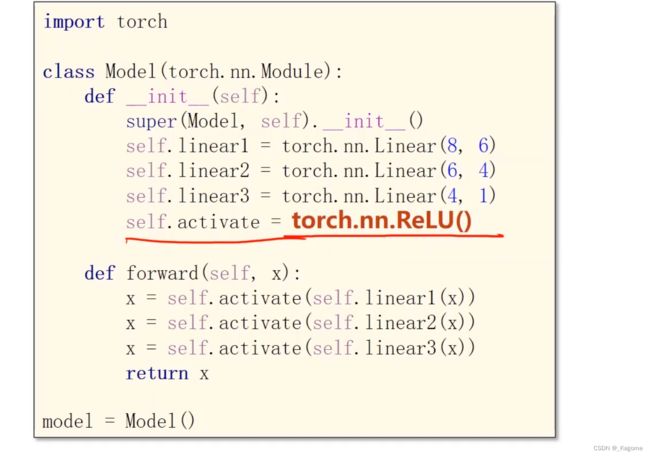
进行修改，把输入的维度改成8，把输出的维度改为1

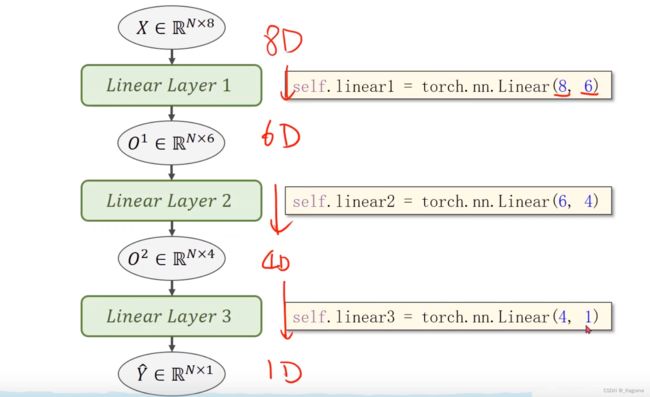
把多个logistics regression进行首尾相连，就可以构成一个多维度的神经网络模型
Eg：此为8入1出的情况

那假如是8入2出呢？这就需要进行两个logistics regression了，这就进行首尾相连，可以从二维下降到一维

这个(8,2)的含义，就是把8维的映射到2维的空间上，linear就是降维的空间运算
sigmod函数是非线性的变换

构建神经网络模型

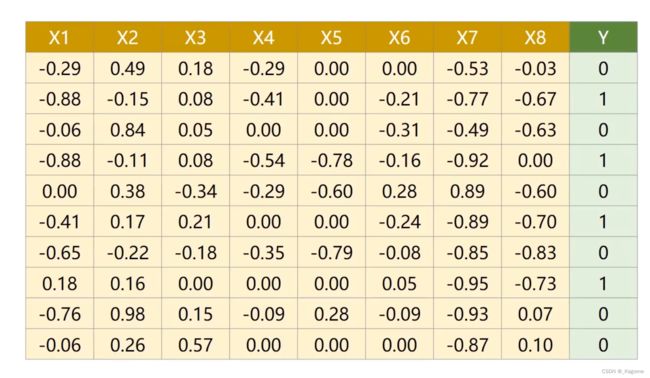
Y表示是否治愈
读取文件，loadtxt，只支持float32
x_data：所有行，一直到最后一列，但是不读取最后一列

构造损失，换成了BCE损失

与之前的回归相差不大，还是三步，前馈，反馈，更新

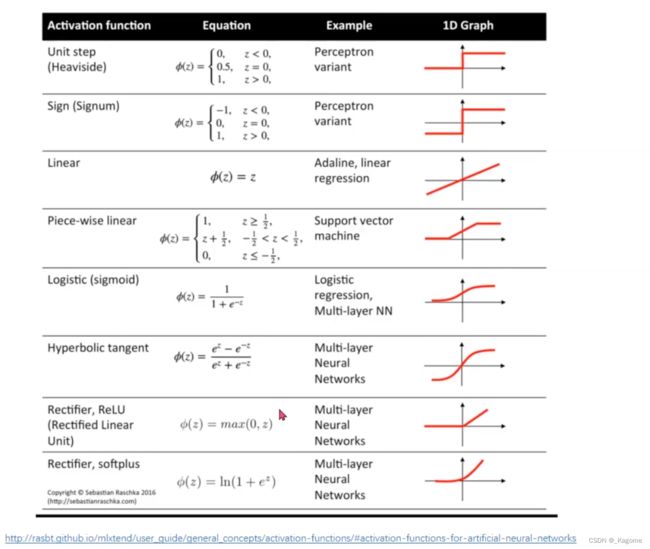
激活函数汇总

ReLu常用，取值为(0,1)
看看谁最后的曲线更优，更快的收敛