对抗样本入门详解

对抗样本基本原理

什么叫对抗样本呢？对抗样本由Christian Szegedy等人提出，是指在数据集中通过故意添加细微的干扰所形成的输入样本，导致模型以高置信度给出一个错误的输出。这样我们可以理解大致的原理是攻击者通过在源数据上增加人类难以通过感官辨识到的细微改变，但是却可以让机器学习模型接受并做出错误的分类决定。比如下面这个奇妙的现象，在原有数据上叠加精心设计的变化量，在肉眼都难以识别的情况下，影响我们模型判断。

什么叫生成对抗网络(Generative Adversarial Nets,GAN)呢？对抗网络有两部分组成，一个是生成器(generator)，一个是辨别器(discriminator),生成器好比一个小偷，而辨别器好比一个警察，小偷的目的是想方设法的欺骗欺骗警察(生成对抗样本)，而警察的目的就是想方设法的去不受欺骗，小偷和警察都在不断的优化自己去达到目的，同时彼此都在对方的“监督”下而提升。GAN更深入的解释

• 这种对抗训练过程与传统神经网络存在一个重要区别。一个神经网络需要有一个成本函数，评估网络性能如何，这个函数构成了神经网络学习内容以及学习情况的基础。传统神经网络需要一个人类科学家精心打造的成本函数。但是，对于生成式模型这样复杂的过程来说，构建一个好的成本函数绝非易事。这就是对抗性网络的闪光之处，对抗网络可以学习自己的成本函数——自己那套复杂的对错规则——无须精心设计和建构一个成本函数。
• 机器学习中，无监督学习一直备受关注，而发展却并不迅速，而生成对抗性网络正是通过深度学习本身的缺陷，利用“欺骗”和“反欺骗”的博弈，实现模型内部的监督学习，

数学描述
$$min\mid \mid x_{adv}-x\mid \mid ,s.t.F(x_{adv})\ne y$$
其中 $x$是真实样本，其类别是$y$.$F$是一个已经训练好的分类器网络。$x_{adv}$就是对抗样本。最小化扰动量（两者的差异），使得分类器判决错误。
分类
1.根据对抗样本的输出是否确定了类别：

• 有目标对抗指定
  $$F(x_{adv})=y_{target}\ne y$$
• 无目标对抗只要分类错误就行
  $$F(x_{adv})\ne y$$

2.根据对攻击网络F的先验知识已知多少：
(1).白盒对抗

• 需要知道网络的损失函数、梯度等

(2).黑盒对抗

• 不需要网络内部知识

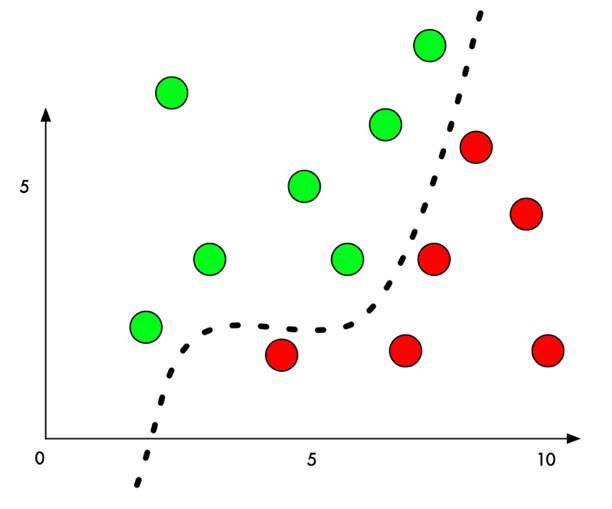
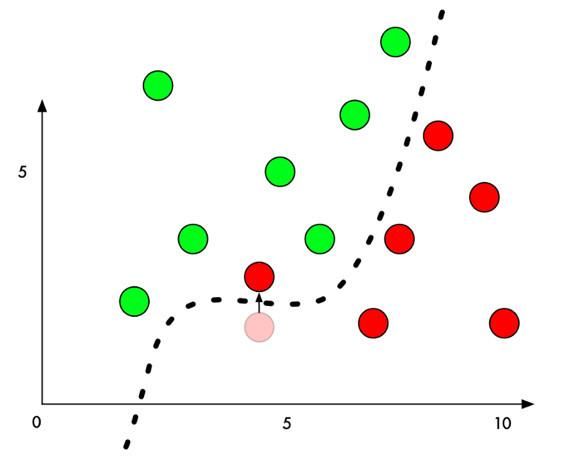
而对抗样本要做的事就是，通过某种算法，针对指定的样本计算出一个变化量，该样本经过修改后，从人类的感觉无法辨识，但是却可以让该样本跨越分割平面，导致机器学习模型的判定结果改变（如下图）。

---

对抗样本的发生

先提前再复习一下过拟合与欠拟合

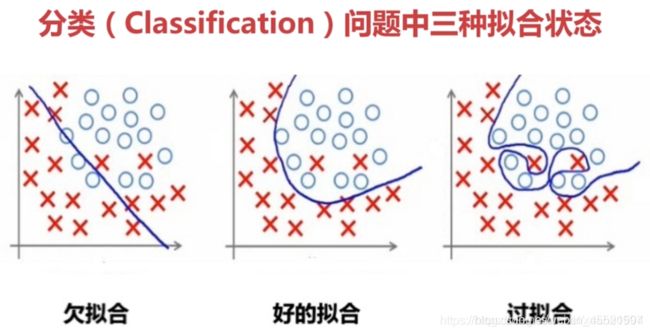
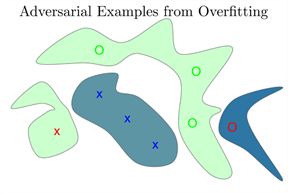
• 过拟合就是训练的时候效果很好损失函数值可以降得很低，但是到测试数据集的时候表现就不那么好了，就是过分依赖于现有训练数据集的特征造成的。对于举个具体的例子方便理解过拟合，图中绿色的圈圈和蓝色的叉叉是训练集中两类。我们有一个过于分类器能非常容易的拟合训练集。绿色的块块就代表分类器认为类是圈圈的范围，蓝色的块块代表分类器认为类是叉叉的范围。可以看到分类器能正确将训练集分类。但是因为分类器过于复杂，用来表示训练集特征空间的参数过多，分类器对没有训练集的特征空间也进行分类，随机的赋予了绿色或蓝色的块块。而就在这些空间中存在着对抗样本，红色的本该是叉叉被误认为是圈圈，红色的本该是圈圈的被误认为是叉叉。
  
  • 解决过拟合的方法：降低数据量，正则化（L1,L2），Dropout（把其中的一些神经元去掉只用部分神经元去构建神经网络）
• 欠拟合(UnderFitting)：样本不够或者算法不精确，测试样本特性没有学到，不具泛化性，拿到新样本后没有办法去准确的判断。举个例子理解欠拟合，对于一个类似的训练集，我们用一个简单的线性模型去拟合，得到的超平面也完美的分割了训练集，但是这个超平面没有掌握训练集真正的结果，圈圈的分布明显是一个弧形，沿着弧线继续采样圈圈，却发现越过了超平面被误分；类似的叉叉的分布也容易越过超平面被误分。
  • 增加训练数据，优化算法
    
    从下面这个图我们可以更能加深对欠拟合和过拟合的认识
    
    

两个说明对抗样本不是过拟合的解释：

• 对抗样本进行测试中导致了错误输出，可能有的人认为过拟合。但是如果是过拟合。复杂的CNN过拟合了训练集，而测试集的分布是未知的，模型必然会出现一些随机性的错误。而我们用不同的模型重新拟合时，应该会看到模型在训练集之外犯不同的错误。但实际上，研究人员发现许多不同的模型对同一个对抗样本会犯同样的错误，如果将一个对抗样本和原图像相减得到在图像空间上的方向向量，用来加上其他任一个图像，几乎都会被误分类。（这一点其实是对抗样本的可移植性，能够在不同的模型下，使模型识别出错）
• Ian Goodfellow 在ICLR2015年的论文中，通过在一个线性模型加入对抗干扰，发现只要线性模型的输入拥有足够的维度（事实上大部分情况下，模型输入的维度都比较大，因为维度过小的输入会导致模型的准确率过低），线性模型也对对抗样本表现出明显的脆弱性，这也驳斥了关于对抗样本是因为模型的高度非线性的解释

上述这些内容可以说明对抗样本出现，不是因为这些图片有着一些脆弱的特点，或者模型对某些属性的过拟合造成的。我们不应该把对抗样本想象成孤立的outliers，可能理解成它们来自对抗样本子空间更为准确。
说了这么多，那对对抗样本的模型误判到底是什么原因其实，合理的解释是欠拟合，由于输入空间维度过高，模型过于线性的结果。但是我们通过对DNN的学习可以知道，我们基本都会在不同层之间加入激活函数（sigma函数，tanh函数以及现在最常用效果更好的relu函数），这样不是和线性没有太大关系吗？

• 深度模型本实确实是一个非常非线性的模型，但是模型的组成部分都是线性的，全连接网络的矩阵乘法是线性的，卷积网络的卷积计算也是计算点乘，线性的，还有序列模型用到LSTM用的是最简单的加法，更是线性的。
• 值得注意的是我们可以说深度学习模型从输入到输出的映射是线性的，但是从模型的参数到输出的映射不是线性的，因为每层的参数，权重矩阵是相乘得到的，这也是深度学习模型不好训练的原因之一，参数和输出的非线性关系。所以针对优化输入的优化问题要比针对模型参数的优化问题要容易得多。

为了比较好的理解模型的线性和跨越决策层，我们来看一个一个在Cifar10数据集上，运用使用的攻击方法是FGSM（Fast Gradient Sign Method）的一个例子，这个方法不以梯度直接作为扰动，而是对梯度去符号，并用一个epsilon控制大小。

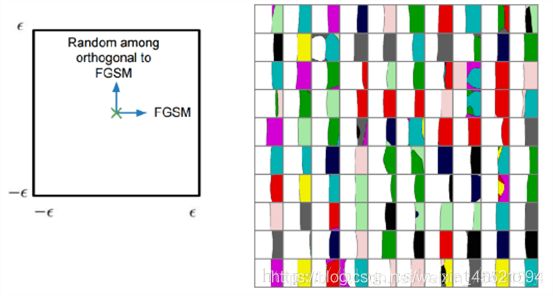
图中右边10x10的网格，每一个块描述了CIFAR-10测试集数据被分类的决策层位置(j决策层是什么？？？)。左边的图示意了每个块内部的意思，块中心表示原图像，没经过修改，往左右移动相当于对图片在FGSM攻击方向修改，上下移动代表对图像进行垂直于FGSM方向的修改。块中白色的区域表示图像被正确分类，其他颜色表示分类错误。可以明显看到，几乎所有块的左半边都被正确分类，而右半边被错误分类，而且分割线是几乎线性的。这于前面分析的可能是欠拟合造成的不谋而合。从这个例子可以知道FGSM确定的方向能有效的得到对抗样本，而且对抗样本应该是存在于线性的子空间中的。打个比方就是，对抗样本和正常样本之间的关系，不像实数和无理数之间的关系，好像每个正常样本边上都能找到对抗样本，而更像是存在与区间中，在这个区间中都是对抗样本。

进一步来说，在高维空间，每个像素值只需要非常小的改变，这些改变会通过和线性模型的参数进行点乘累计造成很明显的变化。而图片通常都有极高的维度，所以不需要担心维度不够。也就是说，只要方向正确，图像只要迈一小步，而在特征空间上是一大步，就能大程度的跨越决策层。

---

对抗样本防御难在哪里

事实上，设计一个好的对抗样本比设计一个能防御对抗样本的模型更简单，下面我们一起来探索一下对抗样本的防御难在哪里。

对抗训练

对抗训练是防御对抗样本攻击的一种方法。将对抗样本和正常样本一起训练是一种有效的正则化，可以提高模型的准确度，同时也能有效降低对抗样本的攻击成功率。不过这种防御也只是针对哪些通过之前训练集产生的对抗样本才有效。（比如用经过FGSM训练的网络，可以有效的防御用FGSM产生的对抗样本攻击，但是如果换其他对抗攻击方法，也会被攻破）

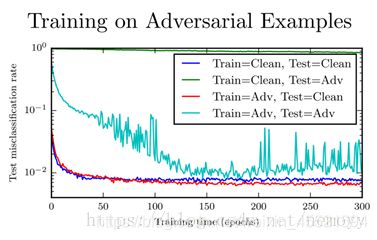
在下面这个图中我们可以清楚地看到（Adv是指加入了对抗样本的数据集，clean是没加对抗样本的正常样本集）训练集是Adv，测试集是
正常样本集的红线的分类误差比训练集和测试集都是正常样本的分类误差小，这说明加入对抗样本的训练集有正则化的效果

隐藏梯度

构造对抗样本的方法一般都是用到模型的梯度，比如想要模型把飞机误认为是船，只需要将飞机的图片往提高分类为船的概率的方向推一把就行。那是不是只要把模型的梯度藏起来，攻击者就往哪个方向推这个飞机了？设想用GoogleAPI得到对飞机的分类结果是99.9%飞机，0.01%的船，那么攻击者就知道，这个飞机的图片比较容易被误分为船，相当于知道了梯度的方向，只需要在自己的模型上往船的方向生成对抗样本就行了。把分类结果改成“飞机”，不给其他可能的类别就能让模型更鲁棒了呢。很遗憾，只要攻击者自己训练一个能输出各类概率的模型，用这个模型生成的对抗样本通常能攻击成功，这也叫黑盒攻击。

defensive distillation

蒸馏是最先由Hinton提出的，通过训练一个模型来预测另一个训练好的模型输出的概率的训练过程。防御性蒸馏只是想让最终模型输出结果更柔和一点。虽然这里的前后两个模型结构相同，第一个模型训练的是硬标签（比如狗的概率是1，猫的概率是0），而第二个模型训练的是软标签（狗0.85，猫0.15），这样后面的这个蒸馏模型对FGSM攻击更具鲁棒性。

其他防御方法还有，对测试样本加入随机噪声，尝试通过autoencoder消除扰动，甚至集成学习，但总的来说，这些基于正则化的尝试最终都被证明没能完全防御。但是据网上报道这些防御方法就有点像打地鼠游戏，填了一个坑，地鼠会从其他坑冒出来。

对抗样本之所以难以防御是因为很难去对对抗样本的生成过程建立一个理论模型。而且生成对抗样本的优化问题是非线性而且非凸的，我们没有掌握一个好的工具去描述这种复杂的优化问题的解，也就很难去想出理论上能解决对抗样本的方法了。从另一个角度，现在的机器学习算法有效的范围只在一个相对小的样本空间中，对比于巨大的样本空间全局，很难要求机器学习算法对空间中每个样本都输出好的结果。

---

对抗样本的生成

对抗样本生成方法介绍

传统的对抗样本生成方法

• 基于梯度的方法代表论文：
  [1] Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. ICLR 2015
  [2] Kurakin A, Goodfellow I, Bengio S. Adversarial examples in the physical world. ICLR 2017
  基本思路：把扰动加在梯度增加的方向，使得模型误判
• 基于优化的方法
  代表论文：
  [3] Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks
  [4] Nicholas Carlini, David Wagner. Towards evaluating the robustness of neural networks. 2017 IEEE Symposium on Security and Privacy (SP)
  基本思路：求解优化问题，用各种变化方法使得优化问题好求解
• 缺点：
  梯度方法快，但是不能保证对抗攻击有效
  优化方法慢，一次只能对一个样本来优化

具体的方法主要有：

• FGSM算法:FGSM由Goodfellow等研究者于2015年提出，他们试图从AI模型的线性角度解释对抗样本存在的原因。假设线性模型权重参数为$w$，输入为$n$，扰动为$ϵ$则新的输出为
  $$w^T\cdot x^{\prime }=w^T\cdot x+w^T\cdot ϵsign(\Delta J_x(x,y,\theta ))$$
  • 这样一来，激活函数输入就相较原始输入增加了$ϵsign(\Delta J_x(x,y,\theta ))$，如果权重w的量级为$m$，其维度为$n$，扰动最大值为$ϵ$，那么对抗样本对激活函数造成的影响即为$ϵmn$，随着维度n的增加，扰动给激活函数输入带来的增量也相应增大，最终将会改变激活函数的输出值。
  • 直观上来看，损失函数对于输入x的梯度是损失函数变化最快的方向。在非指定目标攻击场景下，沿着梯度方向增加像素值将会使得原始类别标签的损失值增大，从而降低模型判定对抗样本为原始类别的概率；
  • 在指定目标攻击场景下，沿着梯度相反方向增加像素值将会使得指定目标类别标签的损失值减小，从而增加模型判定对抗样本为指定目标类别的概率。
• BIM算法:Google Brain的Kurakin等研究者在FGSM的基础上提出了BIM用于快速生成对抗样本。BIM实际上是一个迭代版的FGSM，同样采用Linfinity作为范数约束。
  • 对于非指定目标攻击，作者在每次迭代中使用FGSM生成对抗样本，并加入clip函数用于图片归一化的值域回归，即
    $$x_0^{adv}=x,x_{N+1}^{adv}=C{\mathrm{lip}}_{x,\epsilon }\left\{x_N^{adv}+\alpha \mathrm{sign}\left({\nabla }_x\mathrm{loss}\left(x_N^{adv},y\right)\right)\right\}$$
  • 对于指定目标攻击，作者在迭代中采用类似的方法，即：
    $$x_0^{adv}=x,x_{N+1}^{adv}=C{\mathrm{lip}}_{x,\epsilon }\left\{x_N^{adv}-\alpha \mathrm{sign}\left({\nabla }_x\mathrm{loss}\left(x_N^{adv},t\right)\right)\right\}$$
• 基于迭代的方法有相对较差的迁移性，使得进行黑盒攻击的效果变差。而只有一步的基于梯度的方法虽然白盒攻击的效果不好，但是能产生更具迁移性的对抗样本。
• DeepFool算法：由EPFL的Moosavi-Dezfooli等研究者于2015年提出，收录于2016年CVPR会议中。作为一种白盒对抗样本生成方法，DeepFool原理上由二分类模型出发，计算最小扰动距离为当前输入点到分割超平面的最短距离，推导出二分类任务下的扰动生成方法，并从二分类推广至多分类。DeepFool使用L2范数约束，对抗样本生成效果优于FGSM与JSMA方法，在当时是比较先进的攻击方法。
• JSMA算法：2016年Papernot等研究者基于L0的范数约束，提出了指定目标攻击的JSMA[7]方法用于生成对抗样本。JSMA旨在尽可能减少需要改变的像素点，目标是找到整幅图片中对指定目标具有利的最大显著性像素点，通过改变该像素值的大小，实现基于单像素点的对抗样本生成。
  • 构造了显著性列表(saliency map)用于搜索最佳像素点。如果对于指定目标类别梯度小于0，就增加像素点（就会导致指定目标类别得分低）；对于其他类别，梯度大于0，也增加像素点，使得 其他类别得分增加，反之同理。（相当于导数大于0，增加像素就增加得分；导数小于0增加像素就减少得分）见下图表达式：
    $$S(x,t)[i]=\{\begin{array}{l}0\text{ if }\frac{\partial F_t(x)}{\partial x_i}<0\text{ or }{\sum }_{j\ne t}\frac{\partial F_j(x)}{\partial x_i}>0\\ \left(\frac{\partial F_t(x)}{\partial x_i}\right)\left|{\sum }_{j\ne t}\frac{\partial F_j(x)}{\partial x_i}\right|\text{ otherwise }\end{array}$$

利用GAN生成对抗样本

为什么考虑用GAN来生成对抗样本呢？传统方法让真实图像和生成图像在像素级别上误差最小，但实际上两个图像差一些像素对于整体而言没什么大影响，GAN是保证了整图级别上的相似，例如MNIST数据集中的2，如果拖尾写的长一点，仍然是个2，像素上差别是有的，但是不影响它是个2
用GAN来生成对抗样本，其实就是在原来GAN结构上增加了一个分类器网络F，

• 原来的GAN网络：用于生成对抗样本，使得对抗样本和真实图像非常像（保证对抗样本和真实样本在视觉上无差别）
• 新增加的网络F:就是要攻击的分类器网络，用于判断生成的样本是否能够有效攻击，把损失函数传递给G和D用于训练
  

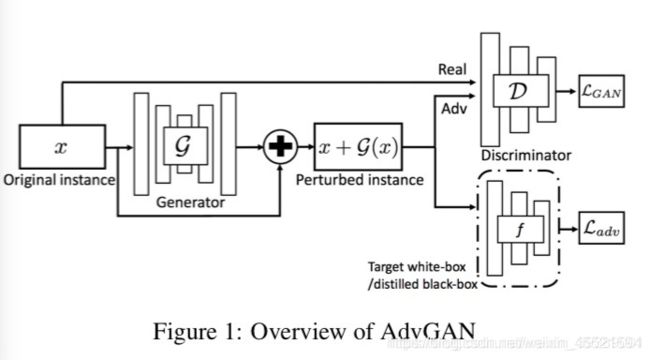
与原始的GAN有两个差别

• [1]是增加了分类器网络F FF
• [2]是原来的GAN的生成$G$的输入是噪声$z$ ，输出图像$G(z)$
  这里用原始样本$x$作为输入，生成的是扰动量$G(x)$,生成的对抗样本$x_{adv}=x+G(x)$

损失函数为
$$L=L_{adv}^F+\alpha L_{GAN}+\beta L_{hinge}$$

• 其中$\alpha$,$\beta$是权重，$L_{adv}^F$,对抗样本在分类器上的损失函数，定义为
  $L_{adv}^F=E_x\left[l_F(x+G(x),t)\right]$其中$t$是目标分类标签，就是上面的$y_{target}$,希望对抗样本$x+G(x)$能够被$F$分类为$t$ ，$L$就是在训练分类器网络$F$时候采用的$loss$（例如交叉熵损失函数）。$L_{\text{hinge}}=E_x[\max \left\{0,\Vert G(x){\Vert }_2-c\right\}$其中$G(x)$就是扰动量，这是为了约束扰动量的$L2$范数不要超过一个给定的上限$c$。

用这个网络来训练G和D，达到均衡时候，把G拿出来用就可以喽！

利用FGSM生成对抗样本代码复现（基于mnist）

特别注意的是在这里用FGSM生成样本时，选择的数据集为batch_size为1

from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
from torchvision import models
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

1.设置初始参数

num_epochs = 5
batch_size =512

2.导入训练集和测试集

# 训练集
trainloader = torch.utils.data.DataLoader(              
        datasets.MNIST('data', train=True, download=False,
                       transform=transforms.Compose([
                           transforms.ToTensor(),       # 图像转化为Tensor
                           transforms.Normalize((0.1307,), (0.3081,))       # 标准化
                       ])),
        batch_size=batch_size, shuffle=True)           

# 测试集
test_loader = torch.utils.data.DataLoader(
        datasets.MNIST('data', train=False, transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=1, shuffle=True)   #训练集生成对抗样本的batch_size=1

3.建立网络

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

4.网络实例化

net = Net().to(device)
optimizer = optim.Adam(net.parameters())
cirterion = nn.CrossEntropyLoss()

def train(net, trainloader, optimizer, cirterion, device, num_epochs):  # cirterion为训练的loss
    net.train()
    net = net.to(device)  # 将网络放到device上
    train_loss = []# 记录batch训练过程中的loss变化
    for epoch in range(num_epochs+1):
        correct, total = 0, 0  # 给正确率，总共训练数目，训练一次时间赋初值
        for batch_idx, (inputs, targets) in enumerate(trainloader):
            inputs, targets = inputs.to(device), targets.to(device)  # 将输入数据标签放到device上
            optimizer.zero_grad()  # 优化器梯度清零
            outputs = net(inputs)  # 训练网络
            loss = cirterion(outputs, targets)  # 计算一个batch的损失
            loss.backward()  # 反向传播
            optimizer.step()  # 优化器更新参数
            train_loss.append(loss.item())  # 记录最终训练误差             
            _, predicted = outputs.max(1)  # 返回outputs每一行最大的值以及序号（序号代表着分类结果对于的那一类）
            total += targets.size(0)  # 不同的每个样本展成的tensor按行排列
            correct += predicted.eq(targets).sum().item()  # 计算目标值与预测值相等的个数（比较两个tensor对于位置数相同的个数）
            if (batch_idx+1) % 30 == 0:
                print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f},train acc：{:.2f}'.format(
                    epoch, batch_idx * len(inputs), len(trainloader.dataset),
                    100. * batch_idx / len(trainloader), loss.item(),100.0*correct/total))
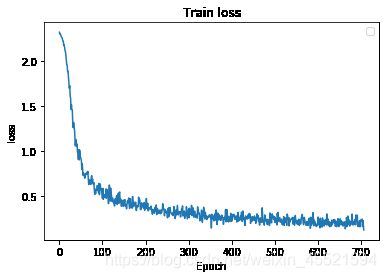
    plt.plot(range(len(train_loss)),train_loss)
    plt.xlabel("Epoch")
    plt.ylabel("loss")
    plt.title("Train loss")
    plt.legend()
    plt.show()

train(net, trainloader, optimizer, cirterion, device, num_epochs)

Train Epoch: 0 [14848/60000 (25%)]	Loss: 1.455892,train acc：31.32
Train Epoch: 0 [30208/60000 (50%)]	Loss: 0.697837,train acc：49.66
Train Epoch: 0 [45568/60000 (75%)]	Loss: 0.572411,train acc：59.55
Train Epoch: 1 [14848/60000 (25%)]	Loss: 0.400240,train acc：85.99
Train Epoch: 1 [30208/60000 (50%)]	Loss: 0.431950,train acc：86.83
Train Epoch: 1 [45568/60000 (75%)]	Loss: 0.337829,train acc：87.43
Train Epoch: 2 [14848/60000 (25%)]	Loss: 0.320007,train acc：90.33
Train Epoch: 2 [30208/60000 (50%)]	Loss: 0.382063,train acc：90.60
Train Epoch: 2 [45568/60000 (75%)]	Loss: 0.294261,train acc：90.67
Train Epoch: 3 [14848/60000 (25%)]	Loss: 0.264269,train acc：92.38
Train Epoch: 3 [30208/60000 (50%)]	Loss: 0.281604,train acc：92.26
Train Epoch: 3 [45568/60000 (75%)]	Loss: 0.300653,train acc：92.31
Train Epoch: 4 [14848/60000 (25%)]	Loss: 0.206523,train acc：93.09
Train Epoch: 4 [30208/60000 (50%)]	Loss: 0.249592,train acc：93.10
Train Epoch: 4 [45568/60000 (75%)]	Loss: 0.207086,train acc：93.31
Train Epoch: 5 [14848/60000 (25%)]	Loss: 0.193962,train acc：94.26
Train Epoch: 5 [30208/60000 (50%)]	Loss: 0.161006,train acc：94.11
Train Epoch: 5 [45568/60000 (75%)]	Loss: 0.191134,train acc：94.10

5.建立对抗样本

epsilons = [0, .05, .1, .15, .2, .25, .3]

# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
    # Collect the element-wise sign of the data gradient
    sign_data_grad = data_grad.sign()
    # Create the perturbed image by adjusting each pixel of the input image
    perturbed_image = image + epsilon*sign_data_grad
    # Adding clipping to maintain [0,1] range
    perturbed_image = torch.clamp(perturbed_image, 0, 1)#将生成的每个像素点限制在0-1之间
    # Return the perturbed image
    return perturbed_image

def test( net, device, test_loader, epsilon ):
 
    # Accuracy counter
    correct = 0
    adv_examples = []
 
    # Loop over all examples in test set
    for data, target in test_loader:
 
        # Send the data and label to the device
        data, target = data.to(device), target.to(device)
 
        # Set requires_grad attribute of tensor. Important for Attack    输入图像也作为模型参数 计算梯度
        data.requires_grad = True
 
        # Forward pass the data through the model
        output = net(data)
        init_pred = output.max(1, keepdim=True)[1] # 得到 max log-probability的序号
 
        # 如果最开始的预测是错误的，就不要攻击继续进行
        if init_pred.item() != target.item():
            continue
 
        # Calculate the loss
        loss = F.nll_loss(output, target)
 
        # Zero all existing gradients
        net.zero_grad()
 
        # Calculate gradients of model in backward pass
        loss.backward()
 
        # Collect datagrad
        data_grad = data.grad.data
 
        # Call FGSM Attack
        perturbed_data = fgsm_attack(data, epsilon, data_grad)
 
        # Re-classify the perturbed image
        output = net(perturbed_data)
 
        # Check for success
        final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
        if final_pred.item() == target.item():
            correct += 1
            # Special case for saving 0 epsilon examples
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
        else:
            # Save some adv examples for visualization later
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
 
    # Calculate final accuracy for this epsilon
    final_acc = correct/float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
 
    # Return the accuracy and an adversarial example
    return final_acc, adv_examples

test( net, device, test_loader, epsilons[1] )

Epsilon: 0.05	Test Accuracy = 8582 / 10000 = 0.8582

• 参考

https://baijiahao.baidu.com/s?id=1602061405148405077&wfr=spider&for=pc
https://blog.csdn.net/winone361/article/details/83684929
https://blog.csdn.net/nemoyy/article/details/81052301
https://blog.csdn.net/xuaho0907/article/details/88649141
《Distilling the knowledge in a neural network》
https://blog.csdn.net/luoyun614/article/details/52202348?
https://blog.csdn.net/PaddlePaddle/article/details/93859690