Apriori算法
文章目录
- 前言
- 先验原理
- Apriori算法的频繁项集产生
- 候选的产生与剪枝
-
- 蛮力方法
- F k − 1 F_{k-1} Fk−1 X F 1 F_{1} F1方法
- F k − 1 F_{k-1} Fk−1 X F k − 1 F_{k-1} Fk−1方法
- 总结
前言
数据挖掘中的关联分析可以分成频繁项集的挖掘和关联规则的生成两个步骤。 A p r i o r i Apriori Apriori算法是挖掘频繁项集的一个经典算法,它开创性地使用基于支持度的剪枝技术,系统地控制候选项项集指数增长。
先验原理
如果一个项集是频繁的,则它的所有子集一定也是频繁的。
为了解释先验原理的基本思想,考虑下图所示的想几个。假定 { c , d , e } \{c,d,e \} {c,d,e}是频繁项集。显而易见,任何包含项集 { c , d , e } \{c,d,e \} {c,d,e}的事务一定包含它的子集(下图中加黑的项集)。因此如果 { c , d , e } \{c,d,e \} {c,d,e}是频繁的,则它的所有子集也一定是频繁的。
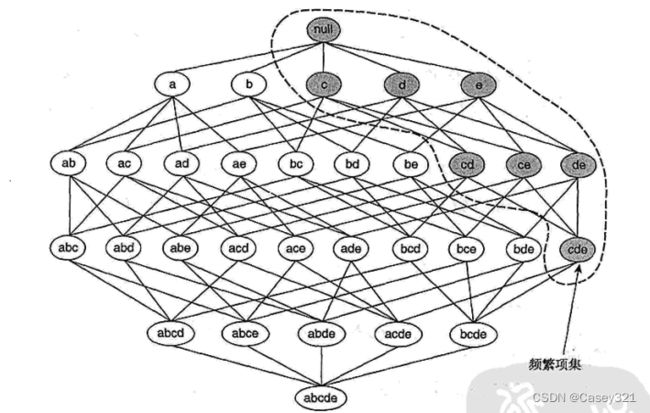
相反,如果项集 { a , b } \{a,b\} {a,b}是非频繁的,则它的所有超集也一定是非频繁的。如下图所示,如果一旦发现 { a , b } \{a,b\} {a,b}是非频繁的,则包含 { a , b } \{a,b\} {a,b}的超集可以被剪枝掉,这样大大减少了搜索空间。这种基于支持度度量修建指数搜索空间的策略称为基于支持度的剪枝(support-based pruning)。这种剪枝策略依赖于支持度度量的一个关键性质,即一个项集的支持度绝不会超过它的子集的支持度。这个性质也称支持度度量的反单调性(anti-monotone)。
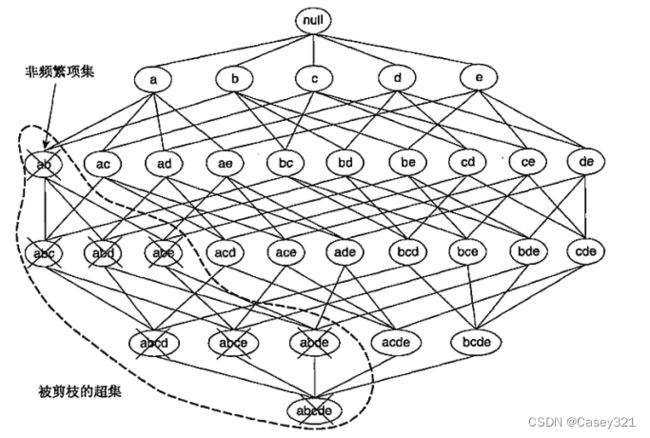
任何具有反单调性的度量都能够直接结合到挖掘算法中,可以对候选项集的指数搜索空间进行有效地剪枝。
Apriori算法的频繁项集产生
以下表为列,假定支持度阈值是60%,即最小支持度(minsup)计数为3。Apriori算法产生频繁项集的过程如下:
| TID | 项 |
|---|---|
| 1 | 面包, 牛奶 |
| 2 | 面包, 牛奶, 啤酒, 鸡蛋 |
| 3 | 牛奶, 尿布, 啤酒, 可乐 |
| 4 | 面包, 牛奶, 尿布, 啤酒 |
| 5 | 面包, 牛奶, 尿布, 可乐 |
-
A p r i o r i Apriori Apriori算法初始将每个项都看做候选1-项集。通过单遍扫描数据集,确定每个项的支持度。如下表所示:红色字体的为频繁1-项集,根据先验原理,支持度低的项(可乐、鸡蛋)将被删除。
候选1项集
| 项 | 支持度 |
|---|---|
| { 啤酒 } | 3 |
| { 面包 } | 4 |
| { 可乐 } | 2 |
| { 尿布 } | 4 |
| { 牛奶 } | 4 |
| { 鸡蛋 } | 1 |
-
接下来,该算法将使用上一次迭代发现的频繁 ( k − 1 ) (k-1) (k−1)-项集通过合并操作产生新的候选k-项集。 为了对候选项的支持度计算,算法需要再次扫描一遍数据集。不断重复上述迭代过程,直到没有新的频繁项集产生。下表分别为候选2-项集、候选3-项集的生成结果(标红的表示是频繁项)。
候选2项集
| 项集 | 支持度 |
|---|---|
| { 啤酒,面包 } | 2 |
| { 啤酒,尿布 } | 3 |
| { 啤酒,牛奶 } | 2 |
| { 面包,尿布 } | 3 |
| { 面包, 牛奶 } | 3 |
| { 尿布, 牛奶 } | 3 |
| 项集 | 支持度 |
|---|---|
| { 面包,尿布,牛奶 } | 3 |
Apriori算法的频繁项集产生的部分有两个重要的特点:
- 它是一个逐层(level-wise)算法,即从频繁1-项集到最长的频繁项集。
- 在每次迭代后,新的候选项都由前一次迭代发现的频繁项集产生,然后通过遍历数据集来对候选项进行支持度计算,并与最小支持度阈值进行比较。
候选的产生与剪枝
- 候选项集的产生。该操作由前一次迭代发生的频繁 ( k − 1 ) (k-1) (k−1)-项集产生新的 k k k-项集。
- 候选项集的剪枝。该操作采用基于支持度的剪枝策略,删除一些候选k-项集。
理论上,存在许多产生候选项集的方法。下面简单介绍几种候选产生的过程。
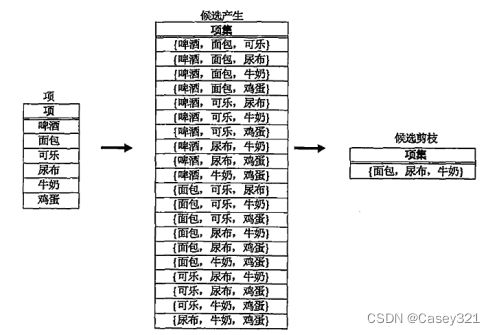
蛮力方法
蛮力方法把所有的k-项集都看作可能的候选,然后使用候选剪枝除去不必要的候选。第 k k k层产生的候选项集的数目为: C d k C_d^k Cdk,其中 d d d是项的总数。虽然候选产生很简单,但是候选剪枝的开销极大。
F k − 1 F_{k-1} Fk−1 X F 1 F_{1} F1方法
下图显示了如何使用频繁1-项集和频繁2-项集产生候选3-项集。
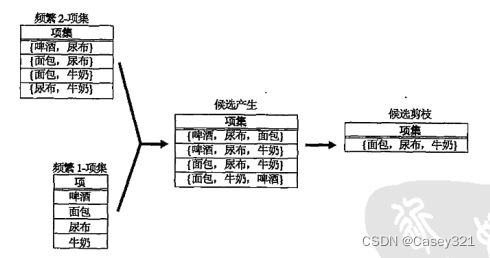
这种方法是完备的,因为每一个频繁k-项集都是由一个频繁 ( k − 1 ) (k-1) (k−1)-项集和一个频繁1-项集组成的。然后,这种方法很难避免重复地产生候选项集。例如, { 面 包 , 尿 布 , 牛 奶 } \{面包,尿布,牛奶\} {面包,尿布,牛奶}不仅可以由项集 { 面 包 , 尿 布 } \{面包,尿布\} {面包,尿布}和 { 牛 奶 } \{牛奶\} {牛奶}合并得到,还可以由 { 尿 布 } \{尿布\} {尿布}和 { 面 包 , 牛 奶 } \{面包,牛奶\} {面包,牛奶}得到等。
而一个避免产生重复的候选项集的一种方法是确保每个频繁项集中的项以 字典序存储。尽管这关方法比蛮力方法有明显改进,但是仍会产生大量不必要的候选项集。
F k − 1 F_{k-1} Fk−1 X F k − 1 F_{k-1} Fk−1方法
该方法合并一对频繁 ( k − 1 ) (k-1) (k−1)-项集,仅当它们的前 k − 2 k-2 k−2个项都相同才能进行合并。
令 A A A = { a 1 , a 2 , ⋯ , a k − 1 } \{a_{1},a_{2},\cdots,a_{k-1} \} {a1,a2,⋯,ak−1} 和 B B B = { b 1 , b 2 , ⋯ , b k − 1 } \{b_{1},b_{2},\cdots,b_{k-1} \} {b1,b2,⋯,bk−1}是一对频繁 ( k − 1 ) (k-1) (k−1)-项集,合并 A A A和 B B B,如果它们满足下面条件:
a i a_{i} ai= b i b_{i} bi ( i = 1 , 2 , ⋯ , k − 2 ) (i = 1,2,\cdots,k-2) (i=1,2,⋯,k−2) 并且 a_{k-1} ≠ \neq = b_{k-1}
例如:频繁项集 { 面 包 , 尿 布 } \{面包,尿布\} {面包,尿布}和 { 面 包 , 牛 奶 } \{面包,牛奶\} {面包,牛奶}合并,形成 { 面 包 , 尿 布 , 牛 奶 } \{面包,尿布,牛奶\} {面包,尿布,牛奶}。算法不会合并项集 { 啤 酒 , 尿 布 } \{啤酒,尿布\} {啤酒,尿布}和 { 尿 布 , 牛 奶 } \{尿布,牛奶\} {尿布,牛奶},因为他们第一个项不同。这个例子表名了候选项产生过程的完全性和使用字典序避免重复的候选的优秀。该方法也是 A p r i o r i Apriori Apriori使用的候选项集生成方法。
总结
A p r i o r i Apriori Apriori算法是在早期成功地处理频繁项集产生组合爆炸问题的算法之一。它通过使用先验原理对指数搜索空间进行剪枝。尽管该算法显著地提高了性能,但是需要多次扫描事务数据集,导致I/O开销较大。对于稠密数据集,随着数据集宽度的增加, A p r i o r i Apriori Apriori算法的性能显著降低。而为了解决这些瓶颈问题,FP-Growth算法随后诞生。