浮点型如何在内存中进行存储呢?
首先,我们先来了解一下,常见的浮点型的表示形式如下所示:
1、3.1415926 —— 浮点数(字面浮点型);
2、1E10=1.0x10^10 —— 浮点数(科学计数法的浮点型);
为了方便讲解,在这里幂次方都使用 ^ 来表示,,不考虑 ^ 在C语言中是按位异或的情况;
浮点数家族包括:float、double、long double类型,其中float类型所占内存空间的大小为:4byte,double和long double类型所占内存空间的大小为:8byte;
浮点型能够表示的范围,以及类型相关的属性,精度,范围等等,都会在#include
整型家族的取值范围,以及类型相关的属性都在#include
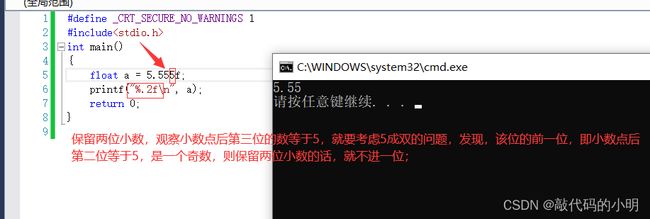
当以float(%f)或者是double(%lf)打印浮点型的数字的时候,都会默认在屏幕上打印出小数点后六位,即使小数点后面一位也没有,它也会自动补充到后六位,但是如果在%f或者是%lf
中的f或lf前,%后面加上 点+数字 ,,,就会控制浮点数在屏幕上打印的小数点后的个数,如果不加的话,%f 和 %lf 都会默认打印出小数点后6位,比如:
首先要知道: 四舍六入五成双
这只适用于保留到小数点后几位的情况,即,保留小数点后几位的位数大于等于1的情况,即,有小数点的情况,遵循四舍六入五成双,
如果是保留到小数点后0位,或者理解成,保留到整数的情况,即遵循四舍五入,要区分开;
所谓四舍六入就和平常所说的是一样的:
1、四舍:
2、六入:
3.五成双:
所谓五成双,即指,如果我们要保留两位小数,那么就观察小数点后第三位,如果是小于等于4,则舍去,如果是大于等于6,则进一位,如果小数点后第三位等于5的话,就要再去观察该位的前一位,即小数点后第二位是不是偶数,是偶数则进一位,是奇数则不进,其中,0我们当做偶数来看;
(1)前一位为奇数:
(2)前一位为偶数:
我们把0当做一个偶数,也要进一位:
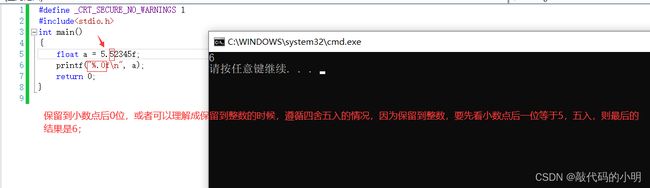
如果是保留到小数点后0位,或者说,保留到整数的话,要遵循四舍五入的规则:
比如:
再或者:
接下来,我们通过一个例子来阐述,整型和浮点型在内存中到底是如何进行存储的?:
int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0; }首先,观察上述代码,应该注意几个地方:
float *pFloat = (float *)&n;
我们取出整型变量n的地址,强制类型转化为float*的类型,这里只是把类型转化了,该地址的值是没有发生变化的,然后再存到float*类型的pFloat指针变量中,我们知道,地址或指针所占
内存空间的大小,只和平台有关,如果平台是32位的,那么,所占内存空间大小就应该是4byte,如果是64位平台,所占内存空间的大小应该是8byte,和地址或指针的类型是没有关系
的,,也就是说,我们是可以把一个整型地址放在一个float类型的指针变量里面去的,一般,我们常使用的平台都是32位平台,他们都占4byte,,所以,是能够放得进去的,在本句代码
里,即使不强制类型转换为float*类型, 也是可以的,,只不过是,类型不匹配,&n的类型应该是int*,放在float*类型中会报警告,但是,是有能力存进去的,运行结果也是正确的,为了
消除警告,我们常常先把类型统一,然后再存放进去;
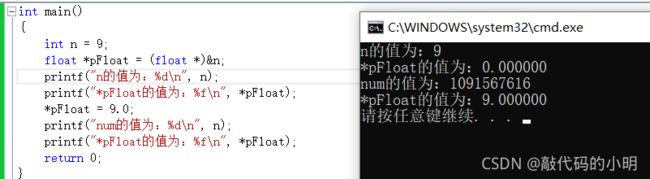
如果不清楚浮点型在内存中的存储方式的话,我们一般会认为,打印出来的结果分别应该是: 9 9.000000 9 9.000000 ,那么,最终的结果会是什么样呢?
我们发现,代码跑出来的答案和我们自己想的有很大的差距:
我们观察第一个结果,,n以整型的形式放进去,然后再以整型%d的形式取出来,结果是9,这是合理的,,第二个结果是,n以整型的形式存进去,然后以%f,浮点型的形式取出来,,
int整型占4byte,float类型也占4byte,float*类型的指针变量pFloat,解引用就会访问4byte,跳过一个float类型,而拿出来的结果是不一样的,不是9.000000,这就说明,浮点型和整型在
内存中的存储方式是不一样的,如果一样的话,拿出来的结果应该是一样的,对于第三个结果,,以浮点型的形式存进去,再以%d整型的形式取出来,结果不是9,这又说明了,浮点型和
整型在内存中的存储方式是不一样的,对于第四个结果,以浮点型的形式存进去,然后以%f浮点型的形式取出来,结果是9.000000,这是合理的;
以整形的视角放进去,再以整型的视角拿出来,,结果是对的,,以浮点型的视角放进去,再以浮点型的视角拿出来,,结果也是对的,,但是混淆放拿结果就是乱的;
我们知道,对于整型来说,整形在内存中是以二进制补码的形式存放的,并且以十六进制进行展示的,那么我们的浮点型在内存中到底是怎么进行存放的呢?
如何将十进制的浮点型数字转化为二进制浮点型数字呢?
法一:
小数点前和小数点后分别进行转化;
小数点前面的进制转换就不再介绍,,,小数点后面的就是:
小数部分乘以2取整,在得到的数的小数部分乘以2再取整,在得到的数的小数部分乘以2再取整,,直到小数部分为0.0结束,然后正序进行排列;
比如:将10进制的0.875转化为2进制的小数:
0.875的小数部分是0.875,
0.875×2=1.75 取整得:1 剩下的小数部分为0.75;
0.75x2=1.5 取整得: 1 剩下的小数部分为0.5;
0.5x2=1.0 取整得: 1 剩下的小数部分为 0.0 ;
小数部分为0.0,到此结束,,正序排列为111,即结果为0.111;
将10进制的65.875转化为2进制:
点前后分别求,,先把点拿出来,,最后直接填数就行 ( A ).( B )
整数部分转换后的二进制记为A,小数部分转换后的二进制记为B;
整数部分: 65.,,,,二进制位1000001 ,,所以A =1000001;
小数部分:0.875
0.875×2=1.75 取整得:1 剩下的小数部分为0.75;
0.75x2=1.5 取整得: 1 剩下的小数部分为0.5;
0.5x2=1.0 取整得: 1 剩下的小数部分为 0.0 ;
小数部分为0.0,到此结束,,正序排列为111,,,这就是10进制小数转为2进制小数的结果,,所以B=111
所以: ( A ).( B ) = (1000001).(111) = 1000001.111
如果,十进制浮点型数字小数点后已经是0.0的话,,那么对应的二进制浮点型数字小数点后直接写 .0 或者二进制浮点型小数点后面不写;
例如: 十进制浮点型数字 9.0 转为 二进制浮点型数字得: 1001或者1001.0 ,,我们一般习惯于写上点以及小数点后面的0,,即,一般常用:1001.0
法二:
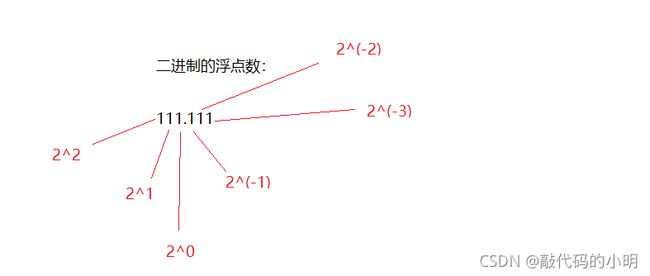
二进制的浮点数:
所以说,十进制的浮点数5.5,,小数点后面的0.5,可以直接用二进制浮点数中的 .1来表示,同理,十进制的浮点数10.875,,小数点后面的0.875,可以直接使用二进制浮点数中的 .111
来表示;
通过上面的内容,我们就可以把任意一个二进制浮点数对应的,S M E 写出来,那么这三个数是怎么进行存储的呢?
我们一直,浮点型家族有:float、double、long double,其中float类型所占内存空间的大小为:4byte,double和long double类型所占内存空间的大小为:8byte,所以,这三者所占内存空
间的大小,分别为,4byte,8byte,8byte,=== 32bit,64bit,64bit;
下图是对于32位的浮点型来说的,即对于float类型来说:
下图是对于64位的浮点型来说的,即对于double或者是long double类型来说:
通过上图,我们就知道,浮点型家族的三个类型对应的S M E 的存储位置是怎么样的了,但是,具体怎么存进去的呢,我们下面来继续探讨:
符号位S来说,只有两种可能,要么是0,要么是1,我们继续来讨论M是如何存储进去的:
对于浮点型数来说,他们没有原码,反码,补码的概念,这个概念只是针对于整型来说的,,整型在内存中是以二进制补码的形式存储的,以十六进制进行展示的,整型在内存中是以补码
的形式存储的,,而我们的浮点型数在内存中是按照上述方法进行存储的,我们根据 IEEE754 标准写出来的二进制序列,就是浮点型在内存中的存储方式;
IEEE 754对有效数字M和指数E,还有一些特别规定:
E为全1的话,得到的E应该是:255或者2047,,这是加上127或者1023得到的值,,所以,E的真实值应该是:128或者1024,,所以,还原到二进制浮点型应该是:
首先,n=9,,9的原码就是:00000000 00000000 00000000 00001001 又因为是正数,,所以,原反补相同,补码也是这个二进制序列,,现在以%d打印,打印的是有符号的十进制整
型,最高位就是符号位,符号位为0,代表一个正数,原反补相同,原码就是该二进制序列,打印出来就是9,整型在内存中是以补码的形式存储的,所以,上述的二进制序列是在内存中的
二进制序列,,也是补码,但是,如果以*pFoat的形式取出的话,是以float浮点型的形式拿出,,首先,浮点型会认为上述的二进制序列也是内存中的二进制序列, 即,上述二进制序列,
如果整型来看的话就是补码,如果浮点型来看的话,就不再考虑原反补的问题了,他是内存中的二进制序列,所以,浮点型也会认为内存中的二进制序列就是上述的二进制序列,站在浮点
数的角度去看这个二进制序列,也是内存中的,他会认为第一个0是符号位,接下来的8个比特位就是E,剩下的23个比特位就是M,,即:0 00000000 00000000000000000001001
所以,S=0,,E全为0,,又因为是float的,所以,E的真实值就是1-127= -126,,,,所以,E的真实值就是 -126 ,,又因E全是0,,所以就在M前面补个 0. 所以,M就是:
0.00000000000000000001001 ,所以,S=0,E= -126 M=0.00000000000000000001001 ,,还原出来的二进制浮点型数字就是:
(-1)^ 0 * 0.00000000000000000001001 * 2^ (-126) ,,得到的就是:0.00000000000000000001001 * 2^ (-126) ,这就是我们的二进制浮点型的数字,,我们以%f 打印的话,要转为
十进制的浮点型数字才可以,,转完之后得到的是: 0.00000000000000000001001 ,小数点往左移动126位,,得到的就是:0.00000000000000000000000000.......0000000001001
这就是我们的十进制的浮点型数字,而,%lf 和 %f 只能默认在屏幕上打印出小数点后6位,,所以,打印在屏幕上的就是:0.000000;
%f 和 %lf 都是以十进制的浮点型打印在屏幕上的;
接下来我们看:*pFloat = 9.0;
已知,,9.0是十进制浮点型数字,,我们要写出他在内存中的存储形式,就要先写出对应的二进制浮点型数字的科学计数法的形式,第一步就是先把该十进制的浮点型数字转为二进制的
浮点型数字,,得到:1001.0,,这就是二进制的浮点型数字,,又等于:1.001 * 2^3,等价于:(-1)^0 * 1.001 * 2^3,,,所以我们得到: S=0 ,M=1.001 E=3,,现在存到二进制
序列中,E要加上127=130,,得到的二进制序列就是: 0 10000010 00100000000000000000000,,这就是十进制浮点型数字9.0在内存中的存储形式,,因为是在内存中的,如果现在
以%d整型的形式取出,并且又是在内存中的二进制形式,所以该二进制序列会被认为成是整型中的补码,,以%d有符号的十进制整型打印,,有符号位,最高位是符号位,最高位是0,
代表正数,原反补相同,所以,原码还是该二进制序列,,打印出来就是:1091567616,,我们知道,整型在内存中是以二进制补码的形式存储,但是以十六进制进行展示,还会涉及到
大小端字节序的问题,如果低位放在低地址上就是小端存储,低位放在高地址上就是大端存储,,那么,浮点型在内存中的存储形式会涉及到大小端字节序的问题吗?
我们知道,十进制浮点数9.0在内存中的存储形式是: 0100 0001 0001 0000 0000 0000 0000 0000,,写成十六进制即为:0x 41 10 00 00,,
我们发现,,即使浮点型在内存中的存储形式不涉及到 原码,反码,补码的概念,浮点型有自己的存储方式,但是仍会涉及到大小端字节序的问题,并且还是小端存储,
我们已经知道,十进制浮点型数字9.0在内存中的存储二进制序列为:0 10000010 00100000000000000000000,,我们再以浮点型的形式取出,,首先,我们要从这个二进制序列中拿出
S M E ,,可得:S=0,,E=3,,M=1.001,,001后面的数省略,本来就是补上去的,拿出来的时候要再舍去,所以,得到科学计数法的表示形式为:(-1)^0 * 1.001 * 2^3,从而得到
1.001 * 2^3,,再得到:1001.0,,这就是二进制浮点型数字,,又因,%f 和 %lf都是以十进制浮点型打印的,所以转为十进制浮点型数字为:9.0,,不够小数点后6位,补齐即得:
9.000000,,这就是我们的答案;
如果以%d整形的形式拿出来,就认为内存中存储的就是补码,,如果以浮点型的形式拿出来,就认为这内存里面存的就是浮点数类型,以浮点数的形式去还原出来;
如果想要以浮点型存入,,整型取出的话,应该写成:
而不是简单的写成;
这样输出的结果和我们的是不一样的,这是因为,我们以浮点型进行存入,,没有经过强制转换,出来的时候的 f 并不是以整型进行取出的,他还是以浮点型进行取出的,,只不过是
以%d打印而已,所以,像这种存入和取出不同类型的时候,一定要有强制转换,没有强制转化就不行;