清风数学建模学习笔记(一)层次分析法
目录
一、基本介绍
二、利用层次分析法解决评价类问题
2.1判断矩阵
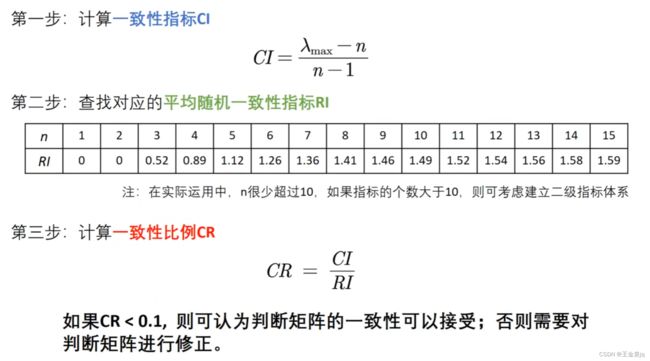
2.2判断矩阵一致性检验
2.3计算权重
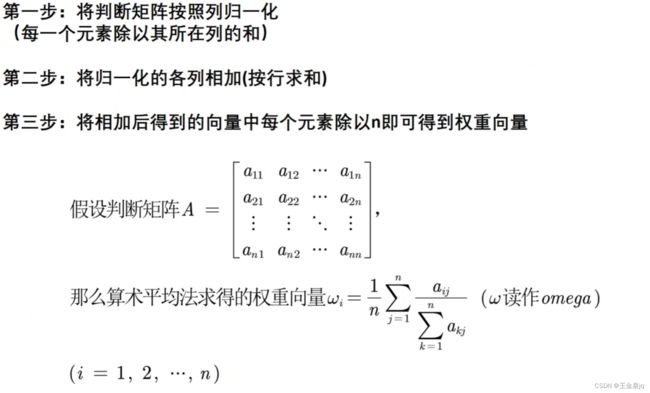
2.4算数平均法求权重
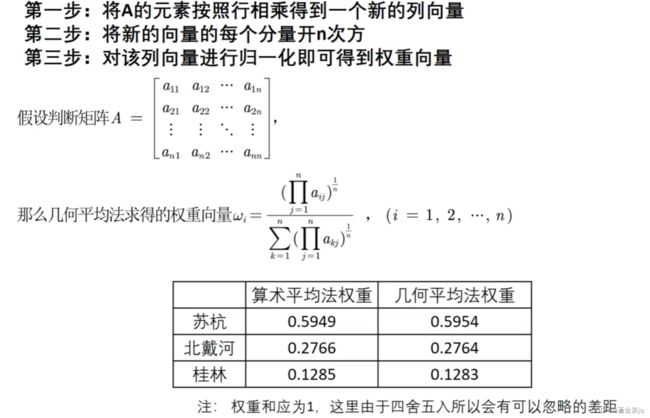
2.5几何平均法求权重
2.6特征值求权重
三、总结
一、基本介绍
层次分析法是评价类模型中的一种常见算法,它是用来根据多种准则,或是说因素从候选方案中选出最优的一种数学方法,例如我们在生活中会遇到各种各样的问题,比如各个高校的对比,旅游景点的选择,都需要我们来根据一定的权重来进行决策,在进行选择,进行决策时我们所想的种种因素都是相互关联和制约的,比如两所高校的教学水平,风景等。层次分析法就是解决这种决策系统的一种方法。将复杂的决策系统层次化,通过逐层比较各种关联因素的重要性来为分析以及最终的决策提供定量的依据。
下面来看一个小例子(引用清风老师视频例子):小明暑假想去补课班,现在面临A和B两个补课班选择,那么面临一个问题,小明是去A还是B呢?这是一种评价类问题,可以用打分来解决。 小明最关系补课班里的学习氛围(0.4)、桌椅设备(0.3)、补习人数(0.2)、学习环境(0.1)。括号里为小明认为的重要程度,其和为1。
小明根据走访调查列出一个权重表格:
| 指标权重 | A | B | |
| 学习氛围 | 0.4 | 0.7 | 0.3 |
| 桌椅设备 | 0.3 | 0.5 | 0.5 |
| 补习人数 | 0.2 | 0.3 | 0.7 |
| 学习环境 | 0.1 | 0.25 | 0.75 |
A最终得分为0.515=0.7×0.4+0.5×0.3+0.3×0.2+0.25×0.1,同理B最终得分为0.485,所以小明最后选择了A补习班。
二、利用层次分析法解决评价类问题
2.1判断矩阵
解决评价类问题首先要想到以下三个问题: 1.评价的目标是什么 2.为了达到这个目标有几种可选的方案 3.评价的准则或者指标
例如小明想去旅游,初步选择为苏杭,北戴河,桂林,根据评价指标形成评价体系来确定一个旅游方案。
前两个问题是显而易见的,第三个问题需要我们通过题目和上网来搜集资料来确定, 假如我们通过搜集资料确定了以下五个指标:
1.景点景色 2.旅游花费 3.居住环境 4.饮食情况 5.交通便利程度
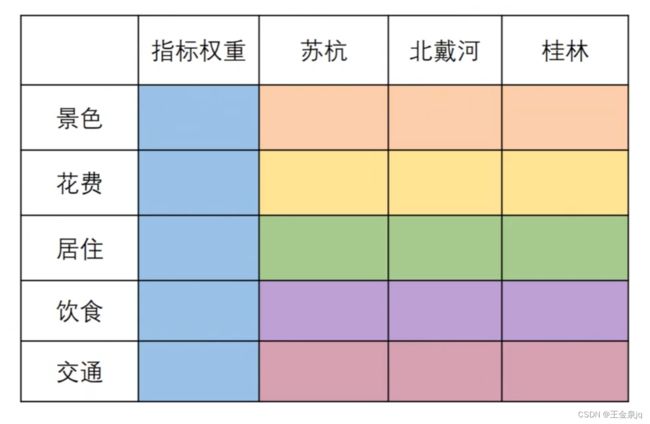
同样,根据第一章的小例子,制作一个权重表格,如下
表格里面的指标权重是不可以随便填写的,在确定影响某因素的诸因子在该因素中所占的比时,遇到的主要困难是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接考虑各因子对该因素有多大程度的影响时,常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的重要性程度不相一致的数据,甚至有可能提出一组隐含矛盾的数据。
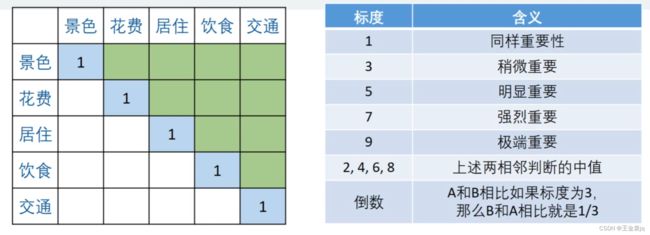
所以,最终决定通过两两比较来进行划分权重,具体如下图:
这里权重表格中的主对角线为1(景色和景色相比同等重要),通过对小明的提问完成左侧表格。首先小明说花费比景色略微重要(介为同等重要1和稍微重要之间就是2),其次对于景色和居住的重要程度相比,景色要比居住重要一点(稍微重要和明显重要一点),由此可见:
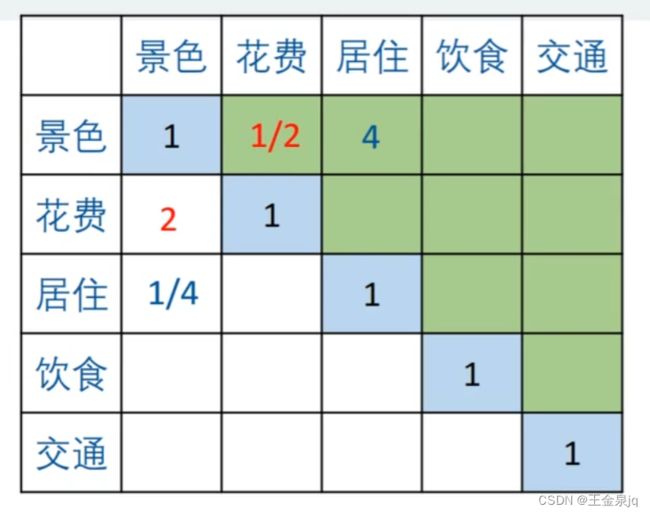
通过小明的十次回答,将表格补充完成,如下:
实际上,上面这个矩阵就是层次分析法的判断矩阵。
2.2判断矩阵一致性检验
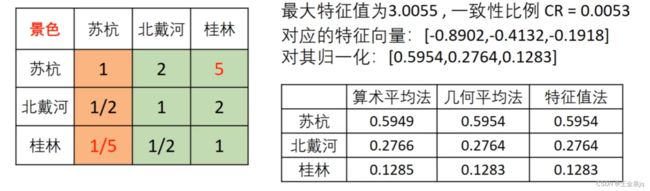
上一小节已经得出了一个权重表格,那么如何根据表格得到三个地点的权重呢?首先如何计算苏杭,北戴河,桂林的景色的权重得分?
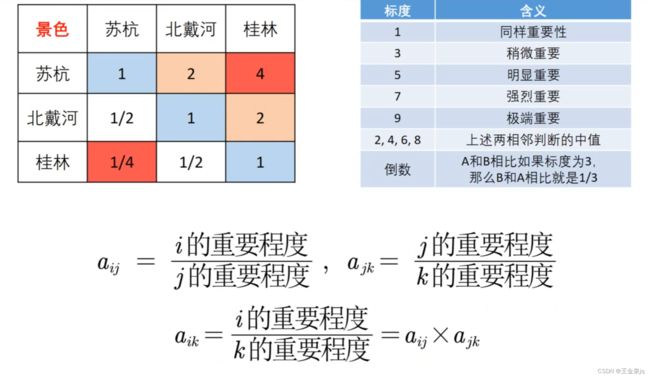
注意,在填写这个判断矩阵的时候会出现一个值得注意的地方,如图
得出一致矩阵的特点:各行各类成倍数关系。
所以在使用判断矩阵求权重之前,必须先对其进行一致性检验。下图是进行一致性检验原理。
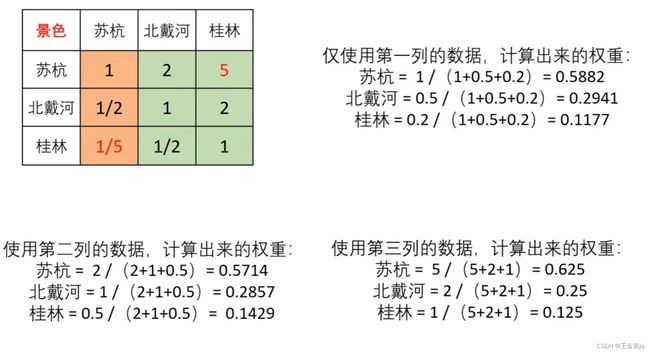
2.3计算权重
一致矩阵计算权重如下(因为每行每列成倍数关系只计算第一列即可):
2.4算数平均法求权重
2.5几何平均法求权重
2.6特征值求权重
假如我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法。
第一步:求出矩阵A的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重
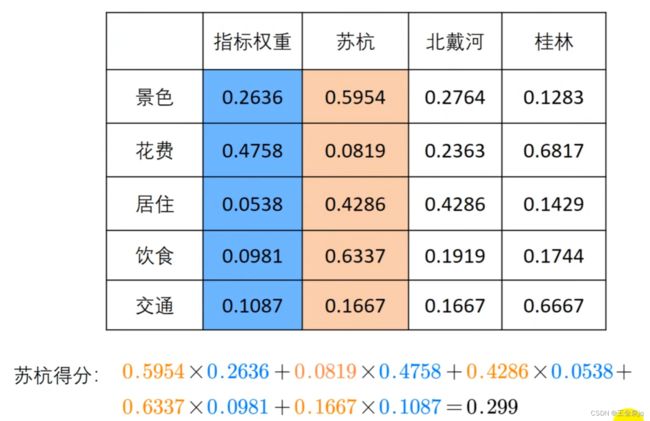
对于上图中的指标权重我们利用最开始的那个权重表格来求解如图:
三、总结
层次分析法:
第一步:分析系统中各因素之间的关系,建立系统的层次结构。
第二步:对于同一层次的各元素关于.上一层次中某一-准则的重要性进行两两比较,构造两两比较 矩阵(判断矩阵)。
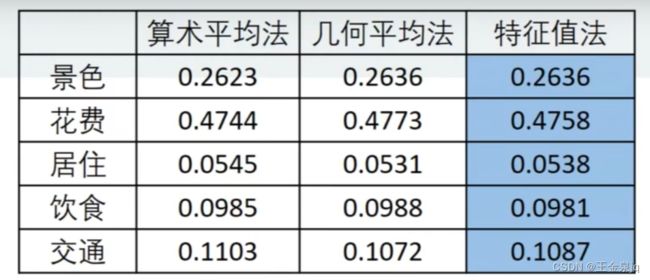
第三步:由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(计算权重的三种方法算数平均、几何平均、特征值)。
以往的论文利用层次分析法解决实际问题时,都是采用其中某一种方法求权重,而不同的计算方法可能会导致结果有所偏差。为了保证结果的稳健性,本文采用了三种方法分别求出了权重,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效。
注:本文章是通过学习清风老师的讲解记录的笔记。