集成学习之GBDT

1、GBDT

1.1 GBDT定义

  GBDT、Treelink、 GBRT(Gradient Boost Regression Tree)、Tree Net、MART(Multiple Additive Regression Tree)算法都是以决策树为基分类器的集成算法，通常由多棵决策树构成，通常是上百棵树且每棵树规模都较小(即树的深度都比较浅)。进行模型预测的时候，对于输入的一个样本实例X，遍历每一棵决策树，每棵树都会对预测值进行调整修正，最后得到预测的结果。假设$F_0$是设置的初值，$T_i$是一颗一颗的决策树。预测结果如下所示：
$$F(X)=F_0+{\beta }_1{T}_1(X)+{\beta }_2{T}_2(X)+\cdot \cdot \cdot +{\beta }_M{T}_M(X)$$
  对于不同的问题和选择的不同损失函数，初值的设定是不同的。比如，对于回归问题并且选择高斯损失函数，那么这个初值就是训练样本的目标的均值。

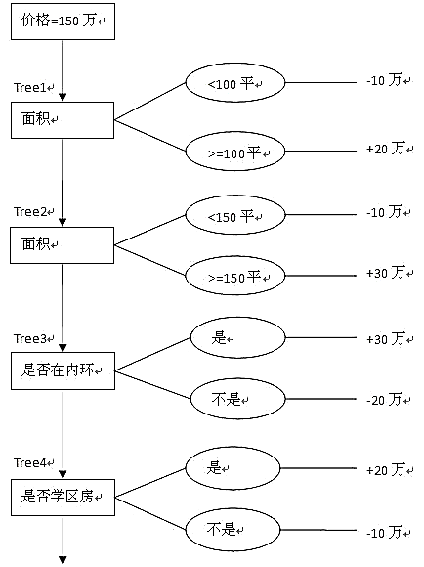
  例如，一套房子有三个价格特征：房子的面积，是否在内环，是否学区房。对于该问题，使用四棵决策树进行预测。初值设为价格的均值，即150万。一个面积120平方米的内环非学区房的价格预测值为$150+20-10=30-10=180万$。这个预测过程如下所示：

1.2 GBDT学习过程

  GBDT也是Boosting算法的一种，但是它和AdaBoost算法不同。区别在于：AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值，然后一轮一轮地迭代；GBDT也要迭代，但是GBDT要求弱学习器必须是CART模型，而且GBDT在模型训练时要求模型预测地样本损失尽可能小。GBDT可直观地理解为：每一轮预测和实际值有残差，下一轮根据残差预测，最后将所有预测相加得到结果。

  GBDT是吧所有树地结论累加起来得到最终结论的，所以可以想到每棵树的结论并不是房价本身，而是房价的一个累加量。每一棵树学习的是之间所有树结论和的残差，这个残差是一个加预测值后得到真实值的累加量。

  GBDT的优点在于，防止过拟合和每一步的残差计算其实变相地增大了分错实例的权重，已经分对的实例则趋向于0.

1.3 GBDT学习过程-例子引入

  通过这个例子看一下GBDT是如何学习一个一个比较小的决策树的。

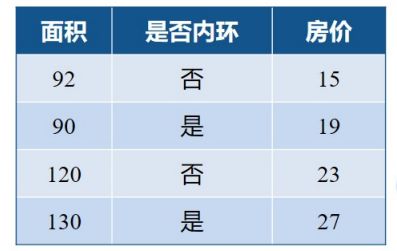
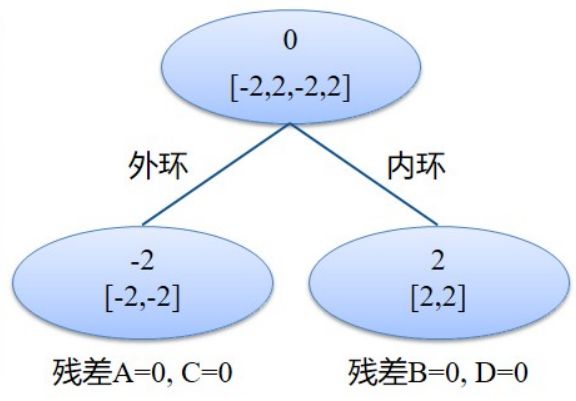
  上面是我们的数据，数据有两个特征，最后一个房价，我们先学习第一颗决策树，我们找使得我们误差最低的一个分类界面，在这里我们找的是面积。

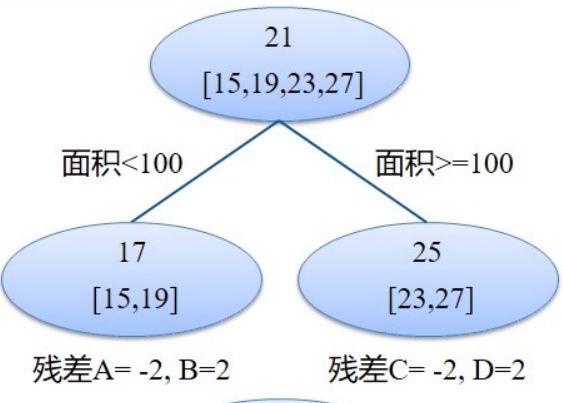
  当面积小于100的时候，我们得到均价17，大于100的时候得到均价25，然后计算真实值和预测值的残差，15-17=-2，19-17=2，23-25=-2，27-25=2.

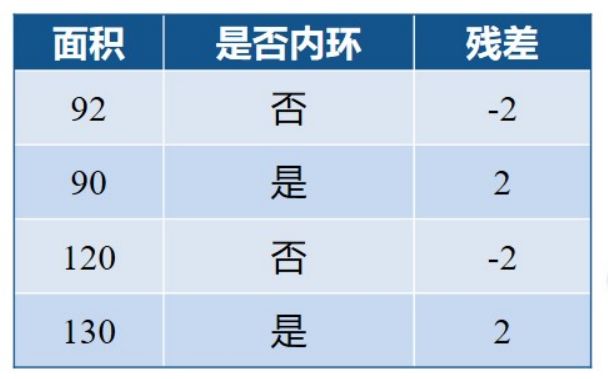
  在学习第二颗决策树的时候。这个时候就不要用原始的数据学习，而是用残差作为输出来学习第二棵决策树，使得残差的误差尽可能小。

  这个时候学习的是是不是外环这个特征，我们是外环的均值为-2，是内环的均值为2，并且计算出相应的残差。这个时候真实值和预测值残渣都是0，这个时候决策树就已经建立好了。

  这个时候我们假设要预测125平方米，内环的房价。

  那么预测房价=25+2=27

1.4 GBDT分类算法

  GBDT的分类算法从思想上与GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

  为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法使用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是**类别的预测概率值和真实概率值的差(数值从0到1的预测)**来拟合损失。
$$\begin{gathered} L(y,f(x))=exp[-yf(x)] \\ L(\theta )=-y_{i}log\widehat{y_i}-(1-y_i)log(1-\widehat{y_i}) \end{gathered}$$

2、代码实战

2.1 GBDT分类

  GBDT实现鸢尾花数据集分类

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd

data_url='data/Iris.csv'
df=pd.read_csv(data_url)

X=df.iloc[:,1:5]
y=df.iloc[:,5]

X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)

clf=GradientBoostingClassifier(n_estimators=100,
                               learning_rate=1.0,
                               max_depth=1,
                               random_state=0)
clf.fit(X_train,y_train)
print('训练集准确率:',accuracy_score(y_train,clf.predict(X_train)))
print('测试集准确率:',accuracy_score(y_test,clf.predict(X_test)))

2.2 GBDT回归

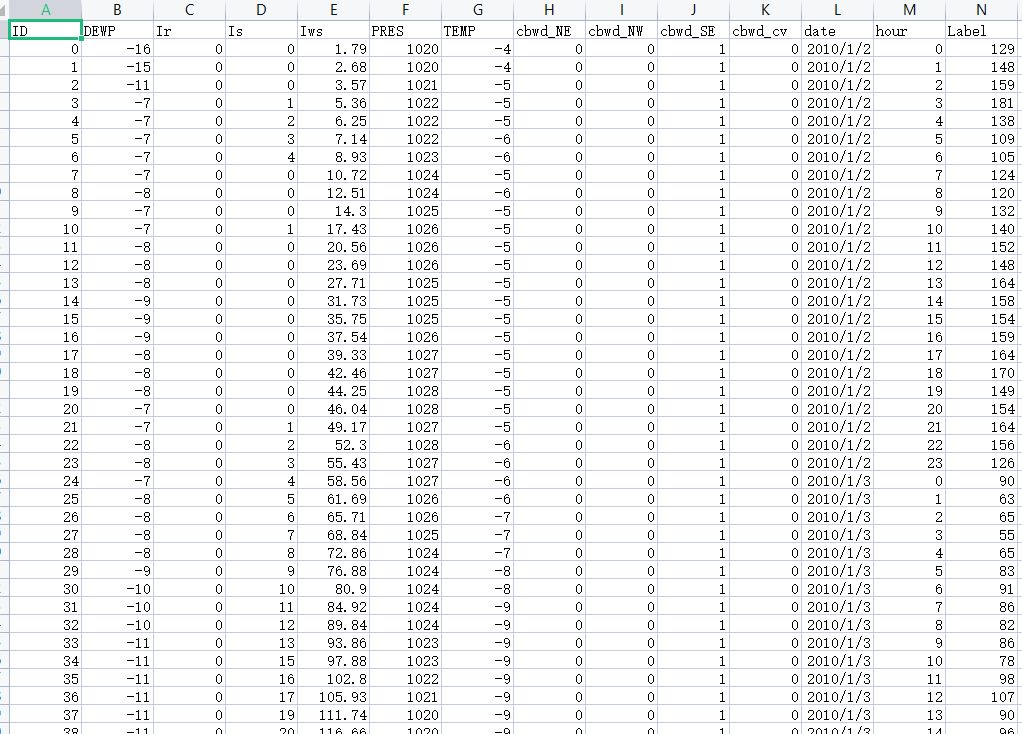
  数据集：

  代码：

import pandas as pd
from sklearn.linear_model import SGDRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error



train_csv='data/trainOX.csv'
train_data=pd.read_csv(train_csv)
train_data.drop(['ID','date','hour'],axis=1,inplace=True)

X=train_data.iloc[:,0:10]
y=train_data.iloc[:,10]

X_train,X_val,y_train,y_val=train_test_split(X,y,test_size=0.2,random_state=42)
reg=make_pipeline(StandardScaler(),SGDRegressor(max_iter=1000,tol=1e-3))

reg.fit(X_train,y_train)

y_val_pre=reg.predict(X_val)
print('Mean squared error:%.2f'% mean_squared_error(y_val,y_val_pre))

只是简单测试算法，更多的参数和指标请自行设置。