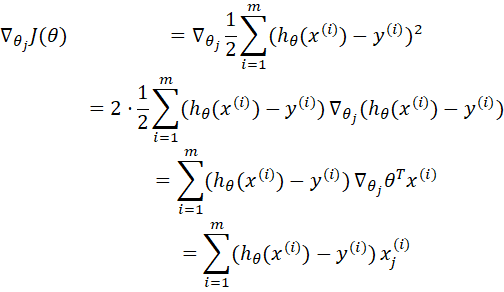【基础机器学习算法原理与实现】使用感知器算法LDA、最小二乘法LSM、Fisher线性判别分析与KNN算法实现鸢尾花数据集的二分类问题
本文设计并实现了PerceptronLA、PseudoIA、LeastSM、LinearDA、KNN等五个算法类,以及DataProcessor的数据处理类。对感知器算法LDA、最小二乘法LSM的伪逆法与梯度下降法、Fisher线性判别分析与KNN算法进行了实现与分析,其中前三种算法都是对一次线性回归的求解。
鸢尾花数据集中第一类鸢尾花“Setosa”和第二类“Versicolor”、第三类“Virginica”的特征分离度非常的高,而第二类“Versicolor”和第三类“Virginica”的分离度很差,即第一类与第二第三类是线性可分的,而第二类和第三类是线性不可分的。因此我们在后续的实验中将以第一类与二三类的分类作为线性可分数据集的实验数据,第二类与第三类的分类作为线性不可分数据集的实验数据。
目录
一、感知器算法
1 感知器算法原理:
(1)线性回归思想
(2)损失函数与损失函数优化
(3)算法步骤
2 感知器算法实现
3 感知器算法结果分析
(1)线性可分数据集的分类
(2)线性不可分数据集的分类
二、 伪逆法算法
1 伪逆法算法原理
2 伪逆法算法实现
3 伪逆法算法结果分析
(1)线性可分数据集的分类
(2)线性不可分数据集的分类
三、最小二乘法算法
1 最小二乘法算法原理
2 最小二乘法算法实现
3 最小二乘法算法结果分析
(1)线性可分数据集的分类
(2)线性不可分数据集的分类
四、Fisher分类算法
1 Fisher分类算法原理
(1)算法原理
(2)算法步骤
2 Fisher分类算法实现
3 Fisher分类算法结果分析
(1)线性可分数据集的分类
(2)线性不可分数据集的分类
五、 KNN算法
1 KNN算法原理
(1)算法思想
(2)算法步骤
2 KNN算法实现
3 KNN算法结果分析
各个算法结果分析
(1)线性可分数据集
(2)线性不可分数据集
一、感知器算法
PLA全称Perceptron Linear Algorithm,即线性感知器算法,属于一种最简单的感知机(Perceptron)模型,是一种可以直接得到线性判别函数的线性分类方法。这里实现的是单样本的感知器算法。
1 感知器算法原理:
(1)线性回归思想
假设我们有m个样本,每个样本拥有n维特征和一个二元类别输出(![]() ),即我们的样本数据为
),即我们的样本数据为![]() 。
。
“感知器”思想的前提是数据是线性可分的,因此我们将函数定义为![]() ,即
,即![]() ,其中
,其中![]() 。(我们在样本中增加一列
。(我们在样本中增加一列![]() ,使得
,使得![]() 能够代表常数项b)
能够代表常数项b)
当此时我们的目标是找出一个满足![]() 的超平面,使得一类样本满足
的超平面,使得一类样本满足![]() ,另一类样本满足
,另一类样本满足![]() ,从而将两类样本分隔开。因此,正确分类的样本即满足
,从而将两类样本分隔开。因此,正确分类的样本即满足![]() ,而错误分类的样本满足
,而错误分类的样本满足![]() 。
。
(2)损失函数与损失函数优化
损失函数的优化目标,就是使得所有误分类的样本满足到超平面的距离之和最小。
观察可知分子和分母都含有 w ,当分子扩大n倍时,分母也将扩大n倍。也就是说,这里的分子分母有着固定的倍数关系。所以我们可以固定分子或分母为1,然后求分子的最小化作为损失函数,这样一来便可以简化我们的损失函数为:![]()
在SGD下的单一样本梯度下降公式为:![]() ,
,
其中i为步长,![]() 为样本输出值1或-1,
为样本输出值1或-1,![]() 为n+1维列向量。
为n+1维列向量。
(3)算法步骤
1. 定义样本,选择解向量w和学习率a的初值
2. 在样本中寻找误分类样本,更新w
3. 循环一定次数或者没有误分类样本时结束循环
2 感知器算法实现
感知器算法被封装在了PerceptronLA类中,分为了初始化,训练,计算损失函数,测试四个函数模块,由于程序每次更新都将计算整体的损失函数,会有非常大的性能开销,如果没有需求可以将计算损失函数模块进行去除。
# 感知机模型
class PerceptronLA:
# 初始化
def __init__(self, a=0.005):
# 将哪一类和其他类分开
self.differentone = clas[differentone]
# 初始化数据矩阵x,增加值为1的x0列来对应方程中的常量系数,也就是b
self.xdata = trainingdata.iloc[:, 0:4]
self.xdata.insert(4, 'x0', 1.0)
# 初始化结果矩阵y
tmp = [-1.0 for i in range(trainingdata.shape[0])]
self.ydata = pd.Series(tmp)
for i in range(trainingdata.shape[0]):
if trainingdata.iloc[i, 4] == self.differentone:
self.ydata.iloc[i] = 1.0
# 初始化解矩阵w
tmp = [np.random.randn() * 0.1 for i in range(5)]
self.w = pd.Series(tmp)
self.w.index = ["sepal.length", "sepal.width", "petal.length", "petal.width", "x0"]
# 学习率,传入或者默认0.1
self.learningRate = a
# count为训练轮数,cont为训练次数
self.count = 0
self.cont = 0
#计算损失函数
def lossf(self, flist, tempw):
LossF = 0
self.cont += 1
for i in range(self.xdata.shape[0]):
sign = self.xdata.iloc[i].dot(self.w) * self.ydata.iloc[i]
if sign < 0:
LossF -= sign
# 利用pla pocket思想,保存当前最优参数,并与修正之后的参数进行结果比较
# 只有当修正之后损失函数更优时才保存新的参数
if len(flist) == 0:
flist.append(LossF)
elif LossF < flist[-1]:
flist.append(LossF)
else :
self.w = tempw
return flist
# 训练
def train(self):
err = 1000
flist = [] #损失函数列表
# 循环两百轮或者没有错误分类的点
while self.count < 500 and err > 0:
err = 0
self.count += 1
# 打乱数据
tmp = [i for i in range(self.xdata.shape[0])]
random.shuffle(tmp)
# 循环
for i in tmp:
# 符号函数sign = y(w*x + b) 用于判断分类是否正确
sign = self.xdata.iloc[i].dot(self.w)*self.ydata.iloc[i]
if sign < 0:
# 如果错在误分类点则进行更新
err += 1
# 梯度下降法优化更新损失函数 w = w + 学习率learningRate * x * y
tempw = self.w + self.learningRate * self.ydata.iloc[i] * self.xdata.iloc[i]
flist = self.lossf(flist,tempw)
# print(self.cont , flist[-1])
# print("第",self.count,"轮pla训练准确率: {:.2%}".format(1 - err / self.xdata.shape[0]))
print("训练轮数: ", self.count)
return flist
# 测试准确率
def test(self):
tdata = testdata.iloc[:, 0:4]
tdata.insert(4, 'x0', 1.0)
cont = 0
sign = tdata.dot(self.w)
for i in range(testdata.shape[0]):
if (sign.iloc[i] > 0 and testdata.iloc[i, 4] == self.differentone) or (
sign.iloc[i] < 0 and testdata.iloc[i, 4] != self.differentone):
cont += 1
print("感知器算法测试准确率: {:.2%}".format(cont / testdata.shape[0]))
3 感知器算法结果分析
由本报告1.3中所述将结果分为线性可分数据集与线性不可分分别讨论。
(1)线性可分数据集的分类
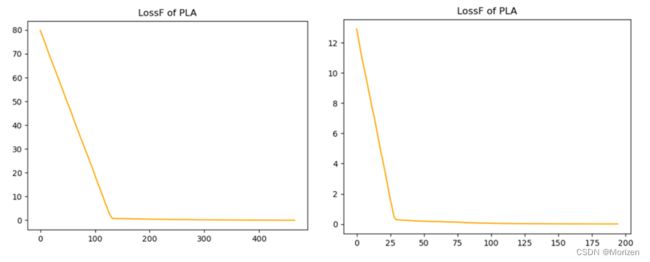
对于线性可分数据集,pla算法能够在指定迭代次数得到结果,迭代次数与初始解向量的随机值有关。准确率保持在100%附近,推测错误原因是感知器算法在特定样本学习下造成的局部最优解问题。准确率表如表2.3.1所示,损失函数变化图如图2.3.1所示:
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
100.00% |
100.00% |
97.78% |
100.00% |
100.00% |
表 pla线性可分数据集准确率
图 pla线性可分数据集损失函数变化图
(2)线性不可分数据集的分类
对于线性不可分数据集,pla算法不能够在指定迭代次数得到结果,迭代次数始终为设定的最大轮数,如损失函数图所示,损失函数在一定轮数优化之后再也无法更近一步的优化了。而测试数据集的准确率在500轮迭代后依旧接近100%,测试数据的准确率主要与测试数据的随机划分相关,虽然训练数据集无法做到100%无误分类点,只要测试数据分布合理准确率还是可以达到100%。
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
100.00% |
96.67% |
93.33% |
96.67% |
100.00% |
表 pla线性不可分数据集准确率
图 pla线性不可分数据集损失函数变化图
二、 伪逆法算法
伪逆法,即用伪逆矩阵对最小二乘法的方程进行求解。
1 伪逆法算法原理
如感知器算法所示,本算法也使用了线性回归的思想与同样的样本结构。使用最小二乘的思想(下一个算法将会对此进行介绍),本算法的损失函数定义为:
对于矩阵X有:![]() (当X是矩阵时,
(当X是矩阵时,![]() 为伪逆矩阵)
为伪逆矩阵)
2 伪逆法算法实现
伪逆法算法被封装在了PseudoIA类中,分为了初始化,求解,测试三个函数模块
# 最小二乘法的伪逆矩阵求解
class PseudoIA:
# 初始化
def __init__(self):
global trainingdata
# 将哪一类和其他类分开
self.differentone = clas[differentone]
# 初始化数据矩阵x,增加值为1的x0列来对应方程中的常量系数,也就是b
self.xdata = trainingdata.iloc[:, 0:4]
self.xdata.insert(4, 'x0', 1.0)
# 初始化结果矩阵y
tmp = [0.0 for i in range(trainingdata.shape[0])]
self.ydata = pd.Series(tmp)
for i in range(trainingdata.shape[0]):
if trainingdata.iloc[i, 4] == self.differentone:
self.ydata.iloc[i] = 1.0
else:
self.ydata.iloc[i] = -1.0
# 初始化解矩阵w
tmp = [0.0 for i in range(5)]
self.w = pd.Series(tmp)
# 求解器:求y = wx这一函数的解
# 最小二乘法所得到的损失函数为函数值与真实y的差的平方和
# 利用矩阵求导可得解w = x的伪逆乘以y
def solver(self):
# 求伪逆矩阵
pidata = pd.DataFrame(np.linalg.pinv(self.xdata.values), self.xdata.columns, self.xdata.index)
self.w = pidata.dot(self.ydata)
# 测试准确率,即拿x乘以w判断正负
def test(self):
tdata = testdata.iloc[:, 0:4]
tdata.insert(4, 'x0', 1.0)
cont = 0
sign = tdata.dot(self.w)
for i in range(testdata.shape[0]):
if (sign.iloc[i] > 0 and testdata.iloc[i, 4] == self.differentone) or (
sign.iloc[i] < 0 and testdata.iloc[i, 4] != self.differentone):
cont += 1
print("伪逆法算法测试准确率: {:.2%}".format(cont / testdata.shape[0]))3 伪逆法算法结果分析
(1)线性可分数据集的分类
伪逆法是稳定求解的算法,对于第一类与二三类的线性可分数据集可以做到100%的准确率。
(2)线性不可分数据集的分类
由于第二三类数据线性不可分特性,根据数据集的随机分类准确率在90%到100%直接跳动。
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
100.00% |
96.67% |
100.00% |
96.67% |
93.33% |
表 pia线性不可分数据集准确率
三、最小二乘法算法
1 最小二乘法算法原理
对于线性回归方程![]() , 回归直线应满足的条件是:全部观测值与对应的回归估计值的误差平方和最小,即
, 回归直线应满足的条件是:全部观测值与对应的回归估计值的误差平方和最小,即 。
。
为了后续推导方便,我们在损失函数前添加1/2的系数得到损失函数:
接下来对损失函数求梯度:
算法步骤按照梯度下降法,即与感知器算法结构类似。
2 最小二乘法算法实现
伪逆法算法被封装在了LeastSM类中,分为了初始化,训练,测试三个函数模块
# 最小二乘法使用梯度下降法进行线性回归
# 由于一般多元的最小二乘法使用正规方程即伪逆矩阵求解,避免重复这里使用梯度下降
class LeastSM:
# 初始化数据
def __init__(self, a=0.0002):
global trainingdata
# 将哪一类和其他类分开
self.differentone = clas[differentone]
# 初始化数据矩阵x,增加值为1的x0列来对应方程中的常量系数,也就是b
self.xdata = trainingdata.iloc[:, 0:4]
self.xdata.insert(4, 'x0', 1.0)
# 初始化结果矩阵y
tmp = [0.0 for i in range(trainingdata.shape[0])]
self.ydata = pd.Series(tmp)
for i in range(trainingdata.shape[0]):
if trainingdata.iloc[i, 4] == self.differentone:
self.ydata.iloc[i] = 1.0
else:
self.ydata.iloc[i] = -1.0
# 初始化解矩阵w
tmp = [np.random.randn() * 0.1 for i in range(5)]
self.w = pd.Series(tmp)
self.w.index = ["sepal.length", "sepal.width", "petal.length", "petal.width", "x0"]
# 学习率,传入或者默认0.1
self.learningRate = a
# 由于是梯度下降,需要使用循环来进行逼近
def train(self):
cont = 0
flist = [] #损失函数列表
# 损失函数为1/2*所有数据函数值和真实值之间的差的平方
# 进行求导后可得梯度wj为函数值h(xi)与真实值yi的差乘以xj的求和(即(h(xi)-yi)xji的求和)
lossF = 1000
while lossF >= 1 and cont <= 5000:
cont += 1
tmp = self.xdata.dot(self.w) - self.ydata
# 损失函数
lossF = tmp.dot(tmp) / 2
flist.append(lossF)
# 梯度下降
self.w = self.w - self.learningRate * tmp.dot(self.xdata)
return flist
# 测试准确率,即拿x乘以w判断正负
def test(self):
tdata = testdata.iloc[:, 0:4]
tdata.insert(4, 'x0', 1.0)
cont = 0
sign = tdata.dot(self.w)
for i in range(testdata.shape[0]):
if (sign.iloc[i] > 0 and testdata.iloc[i, 4] == self.differentone) or (
sign.iloc[i] < 0 and testdata.iloc[i, 4] != self.differentone):
cont += 1
print("最小二乘法算法测试准确率: {:.2%}".format(cont / testdata.shape[0]))3 最小二乘法算法结果分析
(1)线性可分数据集的分类
对于线性可分数据集,lsm算法能够在指定迭代次数得到结果,迭代次数与初始解向量的随机值有关,准确率保持在100%。损失函数变化图如图2.3.1所示:
图 lsm线性可分数据集损失函数变化图
(2)线性不可分数据集的分类
对于线性不可分数据集,lsm算法不能够在指定迭代次数得到结果,迭代次数始终为设定的最大轮数,如损失函数图所示,损失函数在一定轮数优化之后再也无法更近一步的优化了。而测试数据集的准确率在500轮迭代后依旧接近100%,测试数据的准确率主要与测试数据的随机划分相关,虽然训练数据集无法做到100%无误分类点,只要测试数据分布合理准确率还是可以达到100%。
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
100.00% |
96.67% |
96.67% |
93.33% |
100.00% |
表 lsm线性不可分数据集准确率
图 lsm线性不可分数据集损失函数变化图
四、Fisher分类算法
Fisher线性判别分析(Linear Discriminant Analysis, 简称Fisher LDA)是一种应用较为广泛的线性分类方法,该方法于1936年由Fisher提出。
1 Fisher分类算法原理
(1)算法原理
Fisher准则的基本原理是,对于d维空间的样本,投影到一维坐标上,样本特征会混杂在一起,难以区分。如果找到一个投影方向,使得样本集合在该投影方向上最易区分。Fisher准则可描述为用投影后数据的统计性质—均值和离散度的函数作为判别优劣的标准。
(2)算法步骤
2 Fisher分类算法实现
Fisher算法被封装在了LinearDA类中,分为了初始化,求解,测试三个函数模块
# Fisher算法即LDA线性判别分析
class LinearDA:
def __init__(self):
global trainingdata
self.differentone = clas[differentone]
# 初始化数据矩阵x1,x2
t = trainingdata.shape[0]
self.data1 = trainingdata.iloc[0:int(t / classes), 0:4]
self.data2 = trainingdata.iloc[int(t / classes):t, 0:4]
# 初始化解矩阵w,数据类别4类
tmp = [0 for i in range(4)]
self.w = pd.Series(tmp)
self.w.index = ["sepal.length", "sepal.width", "petal.length", "petal.width"]
# 初始化分类阈值
self.w0 = 0
def solver(self):
# 计算样本均值
avdata1 = self.data1.sum(axis=0) / self.data1.shape[0]
avdata2 = self.data2.sum(axis=0) / self.data2.shape[0]
# 计算离散度矩阵
s1 = self.data1 - avdata1
s1 = s1.T.dot(s1)
s2 = self.data2 - avdata2
s2 = s2.T.dot(s2)
sw = s1 + s2
# 最优投影向量
swInv = pd.DataFrame(np.linalg.inv(sw.values), sw.columns, sw.index)
self.w = swInv.dot(avdata1 - avdata2)
# 求出分类阈值w0
avy1 = avdata1.dot(self.w)
avy2 = avdata2.dot(self.w)
self.w0 = (avy1 + avy2) / 2
# 测试准确率,即拿x乘以w判断正负
def test(self):
tdata = testdata.iloc[:, 0:4]
cont = 0
sign = tdata.dot(self.w)
for i in range(testdata.shape[0]):
if (sign.iloc[i] > self.w0 and testdata.iloc[i, 4] == self.differentone) or (
sign.iloc[i] < self.w0 and testdata.iloc[i, 4] != self.differentone):
cont += 1
print("Fish分类算法测试准确率: {:.2%}".format(cont / testdata.shape[0]))3 Fisher分类算法结果分析
(1)线性可分数据集的分类
Fisher分类算法是稳定求解的算法,对于第一类与二三类的线性可分数据集可以做到100%的准确率。
(2)线性不可分数据集的分类
由于第二三类数据线性不可分特性,根据数据集的随机分类准确率在90%到100%直接跳动。推测由于Fisher算法的特性使得其分类稳定度相比前序算法更高。
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
96.67% |
96.67% |
100.00% |
96.67% |
96.67% |
表 Fisher算法线性不可分数据集测试准确率
五、 KNN算法
1 KNN算法原理
(1)算法思想
KNN算法的思路是这样,如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。也就是说,该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。这里我使用了欧氏距离对其进行实现。
(2)算法步骤
1. 计算待分类点与已知点之间的距离
2. 按照距离递增排序
3. 选取距离最近的k个点
4. 返回前k个点出现频率最高的类别作为预测的分类
2 KNN算法实现
KNN算法被封装在了KNN类中,分为了测试,预测两个函数模块
# KNN算法
class KNN:
def __init__(self):
self.difference = clas[differentone]
def predict(self, j):
# 计算欧氏距离
dis = {}
for i in range(trainingdata.shape[0]):
dis[i] = (((trainingdata.iloc[i, 0:4] - testdata.iloc[j, 0:4]) ** 2).sum() ** 0.5)
lis = sorted(dis.items(), key=lambda x: x[1])
# KNN投票
# 计算最近的10个点哪个类型最多并返回类型
cont = [0, 0, 0]
for i in range(10):
if trainingdata.iloc[lis[i][0], 4] == "Setosa":
cont[0] += 1
elif trainingdata.iloc[lis[i][0], 4] == "Versicolor":
cont[1] += 1
else:
cont[2] += 1
return cont.index(max(cont))
def test(self):
cont = 0
for i in range(testdata.shape[0]):
if clas[self.predict(i)] == testdata.iloc[i, 4]:
cont += 1
# elif self.predict(i) > 0 and testdata.iloc[i, 4] != clas[0]:
# cont += 1
print("KNN算法测试准确率: {:.2%}".format(cont / testdata.shape[0]))3 KNN算法结果分析
KNN算法直接对样本所分的三类数据集进行直接分类测试,测试结果的准确率还是相当可观的。根据随机分配的测试数据测试结果如下:
| 运行次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 测试准确率 |
95.56% |
97.78% |
97.78% |
97.78% |
93.33% |
表 KNN算法线性所有数据集分类测试准确率
各个算法结果分析
(1)线性可分数据集
对于线性可分数据集,5种算法都可以得到很好的结果,除了感知器算法在很小一部分的数据集中无法达到100%的测试准确率外,其他算法都能保证在线性可分数据集中保证100%的准确率。对此猜测是由于感知器算法在特定数据集下可能会由于数据集的训练顺序导致产生局部最优的情况。
(2)线性不可分数据集
对于线性不可分数据集,对于大多数数据集5种算法都没有办法达到很好的分类,5种算法的运行准确率表如下:
| 运行次数\算法 |
感知器算法 |
伪逆法算法 |
最小二乘法算法 |
fish分类算法 |
KNN算法 |
| 第1次 |
100.00% |
96.67% |
96.67% |
96.67% |
96.67% |
| 第2次 |
96.67% |
96.67% |
96.67% |
96.67% |
93.33% |
| 第3次 |
100.00% |
100.00% |
100.00% |
100.00% |
96.67% |
| 第4次 |
86.67% |
93.33% |
93.33% |
93.33% |
96.67% |
| 第5次 |
90.00% |
93.33% |
93.33% |
93.33% |
96.67% |
| 第6次 |
100.00% |
100.00% |
100.00% |
100.00% |
93.33% |
| 第7次 |
96.67% |
100.00% |
96.67% |
100.00% |
96.67% |
| 第8次 |
86.67% |
90.00% |
90.00% |
90.00% |
90.00% |
| 第9次 |
93.33% |
93.33% |
93.33% |
93.33% |
96.67% |
| 第10次 |
93.33% |
93.33% |
96.67% |
93.33% |
96.67% |
| 均值 |
90.67% |
93.11% |
93.78% |
93.11% |
94.89% |
| 运行时间(秒) |
34.68 |
0.008 |
2.680 |
0.009 |
1.033 |
表 各个算法在线性不可分数据集中的表现
由表6.1.1可以看出,在线性不可分数据集中都无法保证达到100%的准确率。在这其中,感知器算法的性能最不稳定,平均准确率也最差,但在部分数据集分类下又有很好的表现;KNN算法稳定性最高,平均准确率更高,但是几乎在任何情况下都无法到达100%的准确率。
从运行时间上来看,伪逆法算法与fish分类算法两个直接求解的算法速度最快,而其他三个算法都在同一数量级上(由于感知器算法在每一轮迭代中都计算了损失函数有极大的性能损失,减去其性能损失预估与其他两个算法在同一数量级)。