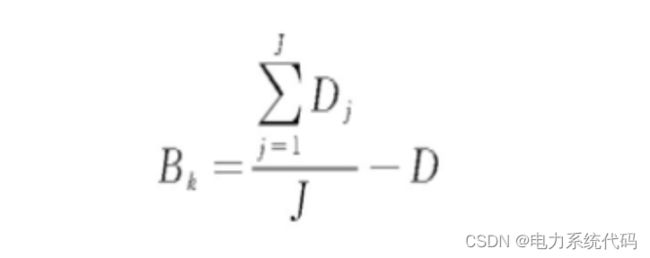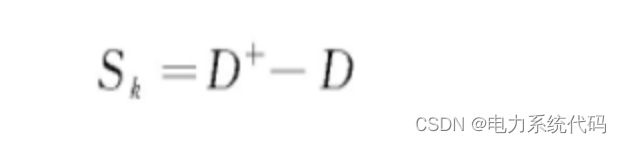蜻蜓优化算法(Matlab完整代码实现)
目录
1 蜻蜓算法概述
2 蜻蜓算法数学模型
2.1 分离
2.2 对齐
2.3 聚集
2.4 食物吸引
2.5 天敌驱散
2.6 程序中的表述
3 完整matlab代码实现
3.1 展现
3.2 Matlab代码
![]()
此算法在电力系统中也有很多应用
1 蜻蜓算法概述
自然充满了执行不同任务的社会行为。尽管所有个体和集体行为的最终目标是生存,但生物在群体、畜群、学校、殖民地和羊群中合作和互动有几个原因:狩猎、防御、导航和觅食。例如,狼群拥有组织最完善的狩猎社交互动之一。狼倾向于遵循社会领导以不同的步骤捕猎猎物:追逐猎物、盘旋猎物、骚扰猎物和攻击猎物 。集体防御的一个例子是海洋中的鱼群。数以千计的鱼类形成了一个鱼群,并通过相互警告来避开捕食者,使得捕食者的捕食变得非常困难。
蜻蜓算法(DA)。 DA算法的主要灵感来源于自然界蜻蜓静态和动态的成群行为。优化、探索和开发的两个基本阶段是通过对蜻蜓在导航、寻找食物和在动态或统计上成群时避开敌人的社会互动进行建模来设计的。接下来文章还考虑了 DA 的二进制和多目标版本的方法,分别称为二进制 DA (BDA) 和多目标 (MODA)。所提出的算法由几个数学测试函数和一个定性和定量的真实案例研究进行了基准测试。该算法能够改善给定问题的初始随机种群,收敛到全局最优,并提供非常有竞争力的结果。 MODA 的结果还表明,该算法倾向于为多目标问题找到具有高度均匀分布的帕累托最优解的非常精确的近似值。潜艇螺旋桨设计问题得到的一组设计证明了MOD的优点。
2 蜻蜓算法数学模型
蜻蜓算法寻优计算主要思路通过模拟蜻蜓的捕食行为来实现(图1),该飞行(进化)寻优机制可以表示为蜻蜓群体分离、对齐、聚集、食物吸引与天敌驱散五个步骤。
2.1 分离
表示避免蜻蜓个体距离太近降低寻优效率:
式中Ek为蜻蜓k的分离度;D表示当前蜻蜓的位置;Dj代表第j个邻近蜻蜓的位置;J代表群体中第k个蜻蜓的邻近蜻蜓的数量。
2.2 对齐
表示某个蜻蜓与其邻近蜻蜓个体速度的相同程度:
式中Uk为蜻蜓k的对齐度;Vj代表第j个邻近蜻蜓的飞行速度;其他符号意义同前。
2.3 聚集
表示某个蜻蜓具有朝着其附近较优蜻蜓个体靠近的趋势:
式中Bk为蜻蜓k的聚集度;其他符号意义同前。
2.4 食物吸引
食物是指某一次迭代计算中最优个体的位置:
式中Sk为蜻蜓k的食物吸引度;D+代表当前计算中最优蜻蜓的位置。
2.5 天敌驱散
目的是使个体尽可能远离最差的蜻蜓个体,提高寻优计算效率:
式中Tk为蜻蜓k的天敌驱散度;D-代表当前计算中最差蜻蜓的位置。
蜻蜓个体k飞行位置更新步长:
蜻蜓飞行位置更新:
式中e、u、b、s、t分别表示分离度、对齐度、聚集度、食物吸引度、天敌驱散度的影响系数;β代表惯性系数;l代表反复迭代计数下标;其他符号意义同前。
2.6 程序中的表述
%====================蜻蜓优化算法的五个步骤===========================
function [Best_score,Best_pos,cg_curve]=DA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)
cg_curve=zeros(1,Max_iteration);
if size(ub,2)==1
ub=ones(1,dim)*ub;
lb=ones(1,dim)*lb;
end
%% 蜻蜓邻域的初始半径
r=(ub-lb)/10;
Delta_max=(ub-lb)/10;
Food_fitness=inf;
Food_pos=zeros(dim,1);
Enemy_fitness=-inf;
Enemy_pos=zeros(dim,1);
X=initialization(SearchAgents_no,dim,ub,lb);
Fitness=zeros(1,SearchAgents_no);
DeltaX=initialization(SearchAgents_no,dim,ub,lb);
for iter=1:Max_iteration
r=(ub-lb)/4+((ub-lb)*(iter/Max_iteration)*2);
w=0.9-iter*((0.9-0.4)/Max_iteration);
my_c=0.1-iter*((0.1-0)/(Max_iteration/2));
if my_c<0
my_c=0;
end
s=2*rand*my_c; % 分离权重
a=2*rand*my_c; % 对齐权重
c=2*rand*my_c; % 聚集权重
f=2*rand; % 食物吸引权重
e=my_c; %天敌驱散权重
for i=1:SearchAgents_no %首先计算所有的目标值
Fitness(1,i)=fobj(X(:,i)');
if Fitness(1,i)Enemy_fitness
if all(X(:,i)lb')
Enemy_fitness=Fitness(1,i);
Enemy_pos=X(:,i);
end
end
end
for i=1:SearchAgents_no
index=0;
neighbours_no=0;
clear Neighbours_DeltaX
clear Neighbours_X
%找到附近的解决方案
for j=1:SearchAgents_no
Dist2Enemy=distance(X(:,i),X(:,j));
if (all(Dist2Enemy<=r) && all(Dist2Enemy~=0))
index=index+1;
neighbours_no=neighbours_no+1;
Neighbours_DeltaX(:,index)=DeltaX(:,j);
Neighbours_X(:,index)=X(:,j);
end
end
%% 分离
S=zeros(dim,1);
if neighbours_no>1
for k=1:neighbours_no
S=S+(Neighbours_X(:,k)-X(:,i));
end
S=-S;
else
S=zeros(dim,1);
end
%% 对齐
if neighbours_no>1
A=(sum(Neighbours_DeltaX')')/neighbours_no;
else
A=DeltaX(:,i);
end
%% 聚集
if neighbours_no>1
C_temp=(sum(Neighbours_X')')/neighbours_no;
else
C_temp=X(:,i);
end
C=C_temp-X(:,i);
%% 食物吸引
Dist2Food=distance(X(:,i),Food_pos(:,1));
if all(Dist2Food<=r)
F=Food_pos-X(:,i);
else
F=0;
end
%% 天敌驱散
Dist2Enemy=distance(X(:,i),Enemy_pos(:,1));
if all(Dist2Enemy<=r)
Enemy=Enemy_pos+X(:,i);
else
Enemy=zeros(dim,1);
end
for tt=1:dim
if X(tt,i)>ub(tt)
X(tt,i)=lb(tt);
DeltaX(tt,i)=rand;
end
if X(tt,i)r)
if neighbours_no>1
for j=1:dim
DeltaX(j,i)=w*DeltaX(j,i)+rand*A(j,1)+rand*C(j,1)+rand*S(j,1);
if DeltaX(j,i)>Delta_max(j)
DeltaX(j,i)=Delta_max(j);
end
if DeltaX(j,i)<-Delta_max(j)
DeltaX(j,i)=-Delta_max(j);
end
X(j,i)=X(j,i)+DeltaX(j,i);
end
else
X(:,i)=X(:,i)+Levy(dim)'.*X(:,i);
DeltaX(:,i)=0;
end
else
for j=1:dim
DeltaX(j,i)=(a*A(j,1)+c*C(j,1)+s*S(j,1)+f*F(j,1)+e*Enemy(j,1)) + w*DeltaX(j,i);
if DeltaX(j,i)>Delta_max(j)
DeltaX(j,i)=Delta_max(j);
end
if DeltaX(j,i)<-Delta_max(j)
DeltaX(j,i)=-Delta_max(j);
end
X(j,i)=X(j,i)+DeltaX(j,i);
end
end
Flag4ub=X(:,i)>ub';
Flag4lb=X(:,i) 3 完整matlab代码实现
3.1 展现
F6:
F12:
F21:
3.2 Matlab代码
clear all
clc
SearchAgents_no=40;
Function_name='F1'; % 测试函数的名称可以从F1换到F23 ( 也可选择自己的目标函数 )。
Max_iteration=500; % 最大迭代次数
%% 所选基准函数的详细信息
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,cg_curve]=DA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
figure('Position',[400 400 560 190])
%% 绘制搜索空间
subplot(1,2,1);
func_plot(Function_name);
title('最优解')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
grid off
%% 目标空间
subplot(1,2,2);
semilogy(cg_curve,'Color','r')
title('收敛曲线')
xlabel('迭代次数');
ylabel('当前最优解');
axis tight
grid off
box on
legend('DA')
display(['DA得到的最优解是 : ', num2str(Best_pos')]);
display(['DA找到的目标函数的最优值是 : ', num2str(Best_score)]);
%====================蜻蜓优化算法的五个步骤===========================
function [Best_score,Best_pos,cg_curve]=DA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)
cg_curve=zeros(1,Max_iteration);
if size(ub,2)==1
ub=ones(1,dim)*ub;
lb=ones(1,dim)*lb;
end
%% 蜻蜓邻域的初始半径
r=(ub-lb)/10;
Delta_max=(ub-lb)/10;
Food_fitness=inf;
Food_pos=zeros(dim,1);
Enemy_fitness=-inf;
Enemy_pos=zeros(dim,1);
X=initialization(SearchAgents_no,dim,ub,lb);
Fitness=zeros(1,SearchAgents_no);
DeltaX=initialization(SearchAgents_no,dim,ub,lb);
for iter=1:Max_iteration
r=(ub-lb)/4+((ub-lb)*(iter/Max_iteration)*2);
w=0.9-iter*((0.9-0.4)/Max_iteration);
my_c=0.1-iter*((0.1-0)/(Max_iteration/2));
if my_c<0
my_c=0;
end
s=2*rand*my_c; % 分离权重
a=2*rand*my_c; % 对齐权重
c=2*rand*my_c; % 聚集权重
f=2*rand; % 食物吸引权重
e=my_c; %天敌驱散权重
for i=1:SearchAgents_no %首先计算所有的目标值
Fitness(1,i)=fobj(X(:,i)');
if Fitness(1,i)Enemy_fitness
if all(X(:,i)lb')
Enemy_fitness=Fitness(1,i);
Enemy_pos=X(:,i);
end
end
end
for i=1:SearchAgents_no
index=0;
neighbours_no=0;
clear Neighbours_DeltaX
clear Neighbours_X
%找到附近的解决方案
for j=1:SearchAgents_no
Dist2Enemy=distance(X(:,i),X(:,j));
if (all(Dist2Enemy<=r) && all(Dist2Enemy~=0))
index=index+1;
neighbours_no=neighbours_no+1;
Neighbours_DeltaX(:,index)=DeltaX(:,j);
Neighbours_X(:,index)=X(:,j);
end
end
%% 分离
S=zeros(dim,1);
if neighbours_no>1
for k=1:neighbours_no
S=S+(Neighbours_X(:,k)-X(:,i));
end
S=-S;
else
S=zeros(dim,1);
end
%% 对齐
if neighbours_no>1
A=(sum(Neighbours_DeltaX')')/neighbours_no;
else
A=DeltaX(:,i);
end
%% 聚集
if neighbours_no>1
C_temp=(sum(Neighbours_X')')/neighbours_no;
else
C_temp=X(:,i);
end
C=C_temp-X(:,i);
%% 食物吸引
Dist2Food=distance(X(:,i),Food_pos(:,1));
if all(Dist2Food<=r)
F=Food_pos-X(:,i);
else
F=0;
end
%% 天敌驱散
Dist2Enemy=distance(X(:,i),Enemy_pos(:,1));
if all(Dist2Enemy<=r)
Enemy=Enemy_pos+X(:,i);
else
Enemy=zeros(dim,1);
end
for tt=1:dim
if X(tt,i)>ub(tt)
X(tt,i)=lb(tt);
DeltaX(tt,i)=rand;
end
if X(tt,i)r)
if neighbours_no>1
for j=1:dim
DeltaX(j,i)=w*DeltaX(j,i)+rand*A(j,1)+rand*C(j,1)+rand*S(j,1);
if DeltaX(j,i)>Delta_max(j)
DeltaX(j,i)=Delta_max(j);
end
if DeltaX(j,i)<-Delta_max(j)
DeltaX(j,i)=-Delta_max(j);
end
X(j,i)=X(j,i)+DeltaX(j,i);
end
else
X(:,i)=X(:,i)+Levy(dim)'.*X(:,i);
DeltaX(:,i)=0;
end
else
for j=1:dim
DeltaX(j,i)=(a*A(j,1)+c*C(j,1)+s*S(j,1)+f*F(j,1)+e*Enemy(j,1)) + w*DeltaX(j,i);
if DeltaX(j,i)>Delta_max(j)
DeltaX(j,i)=Delta_max(j);
end
if DeltaX(j,i)<-Delta_max(j)
DeltaX(j,i)=-Delta_max(j);
end
X(j,i)=X(j,i)+DeltaX(j,i);
end
end
Flag4ub=X(:,i)>ub';
Flag4lb=X(:,i) % 这个函数计算欧氏距离
function o = distance(a,b)
for i=1:size(a,1)
o(1,i)=sqrt((a(i)-b(i))^2);
end
%% 初始化
function Positions=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,2); % 边界数
%% 如果所有变量的边界相等,用户对ub和lb都输入一个标志号
if Boundary_no==1
ub_new=ones(1,dim)*ub;
lb_new=ones(1,dim)*lb;
else
ub_new=ub;
lb_new=lb;
end
%% 如果每个变量具有不同的lb和ub
for i=1:dim
ub_i=ub_new(i);
lb_i=lb_new(i);
Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
Positions=Positions';
%====================目标函数==================
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=10;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=10;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=10;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=10;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=10;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=10;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=10;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=10;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=10;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=10;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=10;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=10;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=10;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
end
function o=Levy(d)
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);
o=0.01*step;