前缀和与差分

---

目录

前缀和

一维前缀和

二维前缀和

差分

一维差分

二维差分

进阶练习NOIP普及组与提高组

---

前缀和

前缀和是一种思想，代码短小精悍是它的特点。相比于数据较大时的从头至尾遍历和优化过的双指针方法来求区间和，前缀和在对于数据进行处理的速度上有着较大的优势，能够以较短的时间求取区间和，极大的优化了时间复杂度。前缀本身就是一种数列的思想。例如我们高中学过的前n项和求Sn，与其不同的是原数列无需满足如等差等比关系，而是任何关系都可以

前缀和算法一般由两个数组构成，a为原数组，s为前缀和数组

一维前缀和的初始化公式:s[i] = s[i - 1] + a[i]

一维区间和的求取公式:ans = s[r] - s[l - 1]

二维前缀和的初始化公式:s[i][j] = s[i-1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]

二维区间和的求取公式:ans = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

一维前缀和

对于一维前缀和来说，顾名思义当然是有一维数组构成的啦

为了方便理解我们可以举个很简单的例子

a数组当中的元素:a[1]，a[2]，a[3]........................................a[n]

s数组当中的元素:s[1]，s[2]，s[3]........................................s[n]

注意下标要从1开始，因为前缀和数组s在初始化的时候方便处理无边界问题，s[0]与a[0]默认为0

那么对于原数组a当中所存的一些元素的值我们不再赘述

对于前缀和数组s，可以列出几项来加强理解

s[1] = s[0] + a[1]

s[2] = s[1] + a[2] = a[1] + a[2]

s[3] = s[2] + a[3] = a[1] + a[2] + a[3] 

由此可见对于前缀和数组当中s中的元素的值是从开头到所在下标的所有原数组元素的和

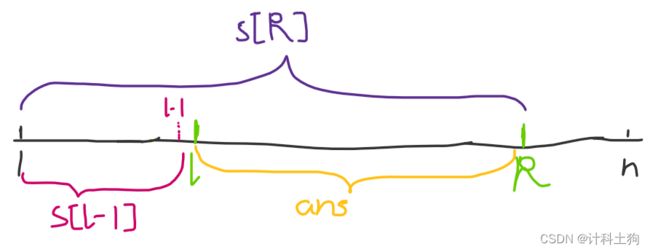
以此来求区间[L,R]上原数组元素的和就简化为了s[R] - s[L - 1]

前缀和

题目描述 

输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。第二行包含n个整数，表示整数数列。接下来m行,每行包含两个整数l和r,表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

1<=l<=r<=n

1<=n,m<=100000

-1000<=数列中元素的值<=1000

样例输入

5 3
2 1 3 6 4
1 2
1 3
2 4

样例输出

3 
6 
10

源代码

#include 
using namespace std;
const int N = 1000000+10;
int a[N],s[N];
int main()
{
	int n,m;
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ )
	{
		cin >> a[i];
		s[i] = s[i - 1] + a[i];
	}
	while(m -- )
	{
		int l,r;
		cin >> l >> r;
		cout<

对应练习AcWing 3127. 来，骗

二维前缀和

一维的时间复杂度优化不明显，对于二维数组的操作，前缀和算法的优势就显得及其突出 

对于二维的数组来说，原数组为a，前缀和数组为s

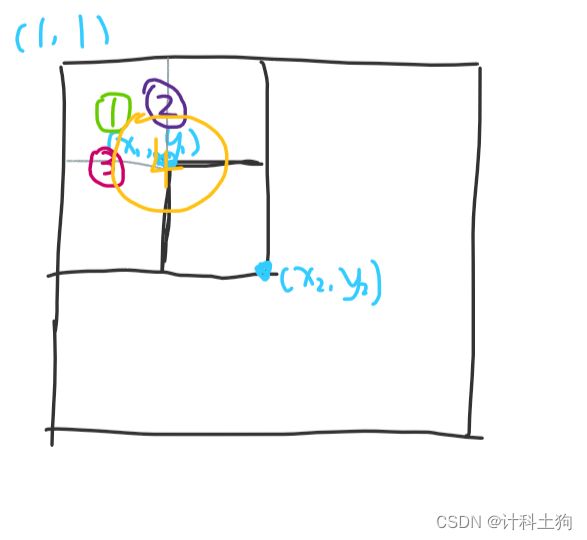
s[x1][y1]、s[x1][y2]、s[x2][y1]、s[x2][y2]所代表的元素之和分别用绿、紫、梅红、黄来表示

利用二维前缀和来求二维数组的区间和

比如(x1,y1)(x2,y2)之间的和则可以用4 - 2 - 3 + 1来表示

换做式子也就是ans = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

对于数组s的初始化则是求从(1,1)到(x,y)的所有元素的和

s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] + s[i - 1][j - 1]

注意下标要从1开始(避免边界问题出现)

s[1][1] = a[1][1]

s[1][2] = a[1][2] + a[1][1]

s[2][1] = a[2][1] + a[1][1]

s[2][2] = a[1][1] + a[1][2] + a[2][1] + a[2][2]

子矩阵的和

题目描述

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。

输入格式

第一行包含三个整数n, m, q。接下来n行，每行包含m个整数,表示整数矩阵。接下来q行，每行包含四个整数x1, y1, x2, y2,表示组询问。

输出格式

共q行，每行输出一个询问的结果。

输入样例

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例

17
27 
21

源代码

#include 
using namespace std;
const int N = 1000+10;
int a[N][N],s[N][N];
int main()
{
	int n,m,q;
	cin >> n >> m >> q;
	for(int i = 1;i <= n;i ++ )
	{
		for(int j = 1;j <= m;j ++ )
		{
			cin >> a[i][j];
			s[i][j] = s[i-1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
		}
	}
	while(q -- )
	{
		int x1,y1,x2,y2;
		cin >> x1 >> y1 >> x2 >> y2;
		cout<

对应练习AcWing 126. 最大的和 

差分

有了前面前缀和的学习之后，就能够更好的理解差分。差分的实质即为前缀和的逆运算，也就是说差分数组在经过自身的前缀和运算之后变成原数组，差分数组常常用来求解对于某一个区间所有元素的操作，大大的优化了时间复杂度与数据处理数量，提高了很高的效率

差分数组有两个数组，a数组为原数组，b数组为差分数组

一维差分的初始化函数

void insert(int l,int r,int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

一维差分的自身前缀和运算

for(int i = 1;i <= n;i ++ )b[i] += b[i - 1];

二位差分的差分初始化函数

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

二位差分的自身前缀和运算

for(int i = 1;i <= n;i ++ )
{
    for(int j = 1;j <= m;j ++ )
    {
        s[i][j] += s[i-1][j] + s[i][j - 1] - s[i - 1][j - 1];
    }
}

一维差分

根据差分和前缀和的性质，对于差分数组b的下标为l加上c的操作等于对于原数组a的下标为l之后的所有元素加上c的操作，由此可见，若是在一维层面上对于区间元素操作则可以解释为

对于a数组[l,r]的区间进行加c的运算可以转化为对于b[l] += c 和b[r + 1] -= c

差分

题目描述

输入一个长度为n的整数序列。接下来输入m个操作，每个操作包含三个整数l,r, c,示将序列中[l, r]之间的每个数加上c。请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数n和m。第二行包含n个整数，表示整数序列。接下来m行，每行包含三个整数l, r, c,表示一个操作。

输出格式

共一行，包含n个整数，表示最终序列。

数据范围

1<=n,m<=100000

1<=l<=r<=n

-1000<=c<=1000

-1000<=整数序列中元素的值<=1000

输入样例

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例

3 4 5 3 4 2

源代码

#include 
using namespace std;
const int N = 1000000+10;
int a[N],b[N];
void insert(int l,int r,int c)
{
	b[l] += c;
	b[r + 1] -= c;
}
int main()
{
	int n,m;
	cin >> n >> m;
	for(int i = 1;i <= n;i ++ )
	{
		cin >> a[i];
		insert(i,i,a[i]);
	}
	while(m -- )
	{
		int l,r,c;
		cin >> l >> r >> c;
		insert(l,r,c);
	}
	for(int i = 1;i <= n;i ++ )b[i] += b[i - 1];
	for(int i = 1;i <= n;i ++ )cout<

对应练习AcWing 2041. 干草堆 

二维差分

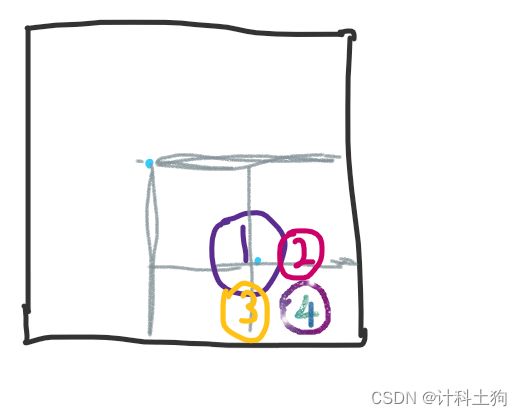
二维差分可以对于从(x1,y1)到(x2,y2)的所有区域进行操作(彩虹笔所标注区域)

 

 

 区域1全部加上c:b[x1][y1] += c

区域2全部减去c:b[x1][y2 + 1] -= c

区域3全部减去c:b[x2 + 1][y1] -= c

区域4全部加上c:b[x2 + 1][y2 + 1] += c

经过这些操作之后可以确保彩虹块内加上了c，而其余区域因加减抵消未发生改变

差分二维数组记得求取自身前缀和运算

差分矩阵

题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, 2, c,其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c,表示一个操作。

输出格式

共n行，每行m个整数,表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,

1≤q≤100000,

1≤x1≤x2≤n,

1≤y1

- 1000< c < 1000,

- 1000≤矩阵内元素的值≤1000

样例输入
 

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1 
1 1 2 2 1 
1 3 2 3 2 
3 1 3 4 1 

样例输出

2 3 4 1
4 3 4 1
2 2 2 2

源代码

#include 
using namespace std;
const int N = 1000+10;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
	b[x1][y1] += c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y1] -= c;
	b[x2 + 1][y2 + 1] += c;
}
int main()
{
	int n,m,q;
	cin >> n >> m >> q ;
	for(int i = 1;i <= n;i ++ )
	{
		for(int j = 1;j <= m;j ++ )
		{
			cin >> a[i][j];
			insert(i,j,i,j,a[i][j]);
		}
	}
	while(q -- )
	{
		int x1,y1,x2,y2,c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1,y1,x2,y2,c);
	}
	for(int i = 1;i <= n;i ++ )
	{
		for(int j = 1;j <= m;j ++ )
		{
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
			cout<

对应练习AcWing3203. 画图

进阶练习NOIP普及组与提高组

P1047 [NOIP2005 普及组] 校门外的树(一维差分)

P2367 语文成绩(一维差分) 

P1830 轰炸III(二维差分)P3397 地毯(二维差分)

P3131 [USACO16JAN]Subsequences Summing to Sevens S(一维前缀和)