【小技巧】STA静态时序分析概述
STA的简单定义如下:套用特定的时序模型(Timing Model),针对特定电路分析其是否违反设计者给定的时序限制(Timing Constraint)。以分析的方式区分,可分为Path-Based及Block-Based两种。
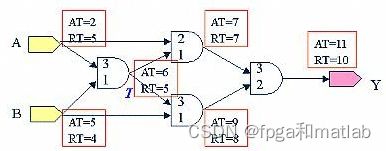
先来看看Path-Based这种分析方式。如图一所示,讯号从A点及B点输入,经由4个逻辑闸组成的电路到达输出Y点。套用的Timing Model标示在各逻辑闸上,对于所有输入端到输出端都可以找到相对应的延迟时间。而使用者给定的Timing Constraint为:
1.讯号A到达电路输入端的时间点为2(AT=2,AT为Arrival Time);
2.讯号B到达电路输入端的时间点为5(AT=5);
3.讯号必须在时间点10之前到达输出端Y(RT=10,RT为Required Time);
现在我们针对P1及P2两条路径(Path)来做分析。P1的起始点为A,讯号到达时间点为2。经过第1个逻辑闸之后,由于此闸有2单位的延迟时间,所以讯号到达此闸输出的时间点为4(2+2)。依此类推,讯号经由P1到达输出Y的时间点为7(2+2+3)。在和上述第三项Timing Constraint比对之后,我们可以得知对P1这个路径而言,时序(Timing)是满足使用者要求的。
按照同样的方式可以得到讯号经由路径B到达输出Y的时间点为11(5+1+3+2),照样和上述第三项Timing Constraint比对,我们可以得知对P2这个路径而言,Timing是不满足使用者要求的。 EDA中国门户网站‑o1DG‑Q@
对图一的设计而言,总共有6个讯号路径。对于采用Path-Based分析方式的STA软体来说,它会对这6个讯号路径作逐一的分析,然后记录下结果。IC设计者藉由检视其分析报告的方式来判断所设计的电路是否符合给定的Timing Constraint。由于最常用来做静态时序分析验证核可(STA Signoff)的EDA软体PrimeTime?采用Path-Based的分析方式,所以本文将以Path-Based的分析方式介绍为主。
再来看看Block-Based的分析方式。此时时序资讯(Timing Information)的储存不再是以路径为单位,而是以电路节点(Node)为单位。由Timing Constraint我们仅能得知A节点的AT为2,B节点的AT为5以及Y节点的RT为10。Block-Based的分析方式会找出每个节点的AT和RT,然后比对这两个数值。当RT的值大于AT时表示讯号比Timing Constrain中要求的时间还早到达,如此则Timing是满足的,反之则不满足。
STA流程及分析方式
STA其分析验证的项目就是我们前文提及之时序检查相关的Timing Arc,如Setup Time、Hold Time等等。以下我们针对Setup Time举实际范例来说明STA的分析方式。 EDA中国门户网站
·Setup Time
设计电路如图所示,时序模型(Timing Model)及时序限制(Timing Constraint)如下:
所有逻辑闸在输出讯号上升时最长的延迟时间为3ns,最短为2ns。
所有逻辑闸在输出讯号上升时最长的延迟时间为2ns,最短为1ns。
所有连线(Net)最长的延迟时间为2ns,最短为1ns。
所有Flip-Flop Clock到Q的延迟时间为3ns。
所有Flip-Flop的Setup Time为1ns(Ts)。
所有Flip-Flop的Hold Time为1ns(Th)。
Clock周期为14ns(Dclkp)。
Clock source latency为2ns(Dclks)。
Clock network latency为3ns(Dclkn)。
Clock uncertainty为1ns(Dclku)。
B及C的input delay皆为1ns(Da、Db、Dc)。
Y的output delay为3ns(DY)。
时序分析的方式。
1.首先找出所有Timing Path,我们只列出具代表性的3条Timing Path来加以说明。
2.假设输入A讯号由0变1,计算第1条Path终点讯号到达的时间(Arrival Time简称AT)。
|
3.假设输入A讯号由1变0,计算第1条Path终点AT。
|
4.计算第1条Path终点的需求时间(Required Time,简称RT)。
|
5.假设输入A讯号由0变1,计算第1条Path终点的Slack。Slack等于RT和AT的差值,对于Setup Time验证来说等于RT - AT,对于Hold Time验证来说等于AT - RT。在此Setup Time范例中,Slack为正,表示讯号实际到达Path终点时间比必须到达的时间还早,因此Timing是满足的。
6.假设输入A讯号由1变0,计算第1条Path终点的Slack。Slack为正,因此Timing是满足的。
|
综合5和6,第1条Path的Timing是符合规格的,其Slack为4ns(取较差状况)。
7.假设前级Flip-Flop的讯号由0变1,计算第2条Path终点的AT。
|
8.假设前级Flip-Flop的讯号由1变0,计算第2条Path终点的AT。
|
9.计算第2条Path终点的RT
|
10. 假设前级Flip-Flop的讯号由0变1,计算第2条Path终点的Slack。Slack为负,因此Timing不满足。
|
11.假设前级Flip-Flop的讯号由1变0,计算第2条Path终点的Slack。Slack为负,因此Timing不满足。
|
综合10和11,第2条Path的Timing不满足,其Slack为-3。
12.假设前级Flip-Flop的讯号由0变1,计算第3条Path终点的AT。
|
13. 假设前级Flip-Flop的讯号由1变0,计算第3条Path终点的AT。
|
14. 计算第3条Path终点的RT。
|
15.假设前级Flip-Flop的讯号由0变1,计算第3条Path终点的Slack。Slack为负,因此Timing不满足。
|
16.假设前级Flip-Flop的讯号由1变0,计算第3条Path终点的Slack。Slack为负,因此Timing不满足。
|
综合15和16,第3条Path Timing不符合规格,其Slack为-4。
打开实现分析工具
显示时序分析软件
其左下角为时序分析的选项