朴素贝叶斯算法之鸢尾花特征分类【机器学习】【伯努利分布,多项式分布,高斯分布】
文章目录
- 一.前言
-
- 1.1 本文原理
- 1.2 本文目的
- 二.实验过程
-
- 2.1使用BernoulliNB(伯努利分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析;
- 2.2 使用MultinomailNB(多项式分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析
- 2.3 使用GaussianNB(高斯分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析;
- 2.4 总结
一.前言
1.1 本文原理
1.熟悉机器学习之朴素贝叶斯算法
2.使用朴素贝叶斯算法解决问题
贝叶斯定理是关于随机事件a和B的条件概率(或边际概率)的定理。其中p(a | B)是当B发生时a发生的可能性。
朴素贝叶斯算法:
对于样本集:
![]()
其中m表示有m个样本,N表示有N个特征。yi,i=1,2,。。,M表示样本类别,值为{c1,C2,…,ck}。
朴素贝叶斯分类的基本公式:
![]()
计算先验概率:计算样本类别数k。对于每个样本y=ck,计算P(y=ck)。这是总样本集中CK类的频率。
计算条件概率:将样本集划分为k个子样本集,分别计算属于CK的子样本集,计算特征概率P(Xj=ajl|Y=Ck)。它是子集中特征值为AJL的样本数与子集中样本数的比率。
对于要预测的样本xtest,计算每个类别CK的后验概率:
![]()
1.2 本文目的
- 使用BernoulliNB(伯努利分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析; 参考代码:bayes =naive_bayes.BernoulliNB()
- 使用MultinomailNB(多项式分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析
- 使用GaussianNB(高斯分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析;
二.实验过程
2.1使用BernoulliNB(伯努利分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析;
和前几篇一样,先使用load_iris模块,里面有150组鸢尾花特征数据,我们可以拿来进行学习特征分类。
如下代码:
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
引入朴素贝叶斯算法模块:
from sklearn import naive_bayes
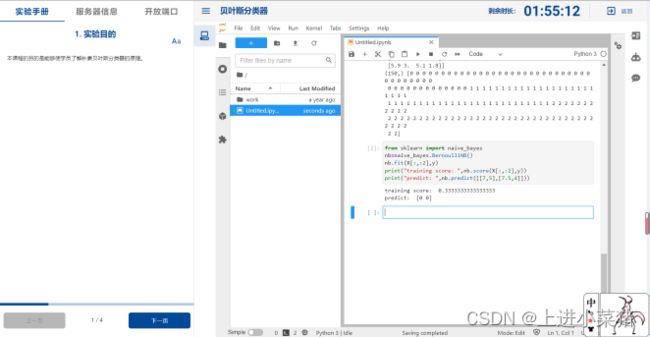
使用朴素贝叶斯算法机器分类器:BernoulliNB的用法如下:(伯努利分布)
nb=naive_bayes.BernoulliNB()
先采用俩个特征集,给鸢尾花分类,输出训练得分和预测,如下代码:
nb.fit(X[:,:2],y)
print("training score: ",nb.score(X[:,:2],y))
print("predict: ",nb.predict([[7,5],[7.5,4]]))
2.2 使用MultinomailNB(多项式分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析
首先,上面的步骤肯定已经做完了,我们接下来在之前的基础上,使用MultinomailNB给鸢尾花特征分类
先保证朴素贝叶斯算法naive_bayes成功引入:
from sklearn import naive_bayes
还有就是load_iris模块,这里省略。
我们使用多项式分布MultinomailNB分类器,如下代码:
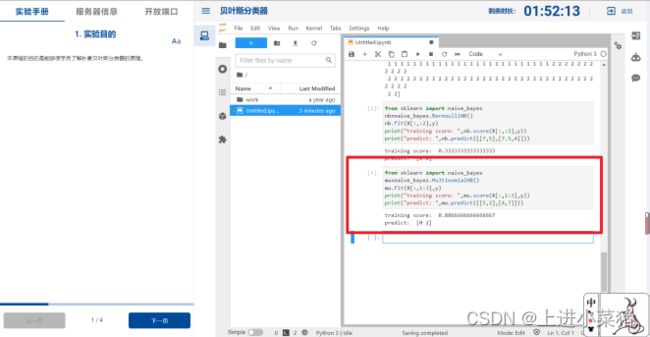
mu=naive_bayes.MultinomialNB()
标准如下:
naive_bayes.MultinomialNB(alpha=1.0,
fit_prior=True,
class_prior=None)
alpha:浮点可选参数。默认值为1.0。实际上,它添加了拉普拉斯平滑,即λ,如果该参数设置为0,则不添加平滑;
fit_prior:布尔可选参数。
是输出为类别K的训练集样本数。
class_prio:可选参数。默认值为“无”。
这里我们选择使用第2,3特征进行鸢尾花特征分类,代码如下:
mu.fit(X[:,1:3],y)
给鸢尾花分类,输出训练得分和预测,如下代码:
print("training score: ",mu.score(X[:,1:3],y))
print("predict: ",mu.predict([[5,2],[4,7]]))
2.3 使用GaussianNB(高斯分布)给鸢尾花分类,写出代码,对运行结果截图并对分类结果进行分析;
我们接下来在之前的基础上,使用GaussianNB给鸢尾花特征分类
先保证朴素贝叶斯算法naive_bayes成功引入:(省略),还有就是load_iris模块,这里省略。
我们使用多项式分布GaussianNB分类器,如下代码:
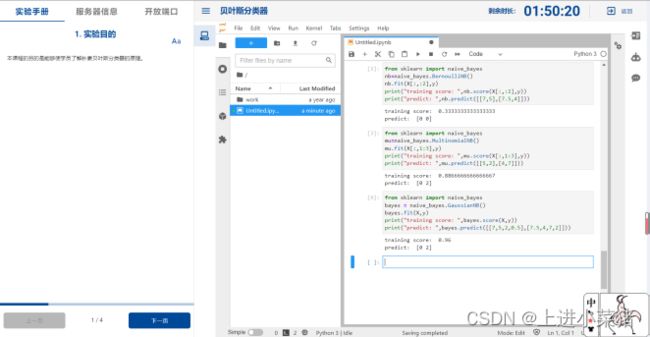
bayes = naive_bayes.GaussianNB()
这里我们选择使用第全特征进行鸢尾花特征分类,代码如下:
bayes.fit(X,y)
给鸢尾花分类,输出训练得分和预测,如下代码:
print("training score: ",bayes.score(X,y))
print("predict: ",bayes.predict([[7,5,2,0.5],[7.5,4,7,2]]))
2.4 总结
需要充分的了解了贝叶斯定理和朴素贝叶斯算法的相关内容。初步可以使用BernoulliNB(伯努利分布),MultinomailNB(多项式分布),GaussianNB(高斯分布)给鸢尾花分类。
主要:
1.熟悉机器学习之朴素贝叶斯算法
2.使用朴素贝叶斯算法解决问题