python数据分析实战之异常值处理

1、异常值定义

在统计学中，离群点是并不属于特定族群的数据点，是与其它值相距甚远的异常观测。离群点是一种与其它结构良好的数据不同的观测值。

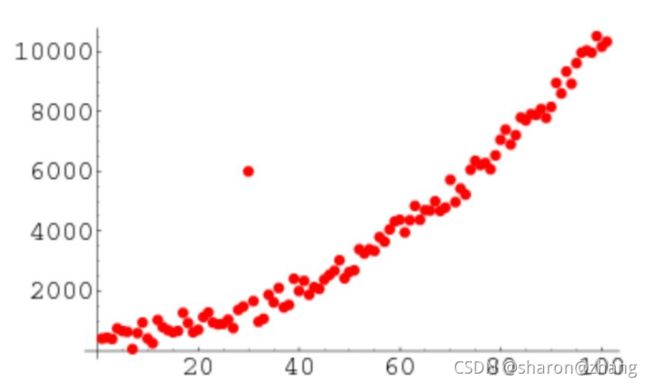
例如，你可以很清楚地看到这个列表中的离群点：[20,24,22,19,29,18,4300,30,18]

当观测值是一堆数字且都是一维时，辨别离群点很容易，但如果有数以千计的观测值或数据是多维的，你可能会需要更机智的方法来检测这些离群点。

2、异常值处理方式

2.1 均方差

3σ原则
如果数据服从正态分布，在3σ原则下，异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。
在正态分布下，距离平均值3σ之外的值出现的概率为 P(|x-μ|>3σ)<=0.003，属于极个别的小概率事件。
如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述

这个原则有个前提条件：数据需要服从正态分布

在3∂原则下，如果观测值与平均值的差值超过3倍标准差，那么可以将其视为异常值。
正负3∂的概率是99.7%，那么距离平均值3∂之外的值出现的概率为P(|x-u| > 3∂) <= 0.003，属于极个别的小概率事件。

import numpy as np
import pandas as pd

def detect_outliers(data,threshold=3):
    mean_d = np.mean(data)
    std_d = np.std(data)
    outliers = []
    
    for y in data_d:
        z_score= (y - mean_d)/std_d 
        if np.abs(z_score) > threshold:
            outliers.append(y)
    return outliers

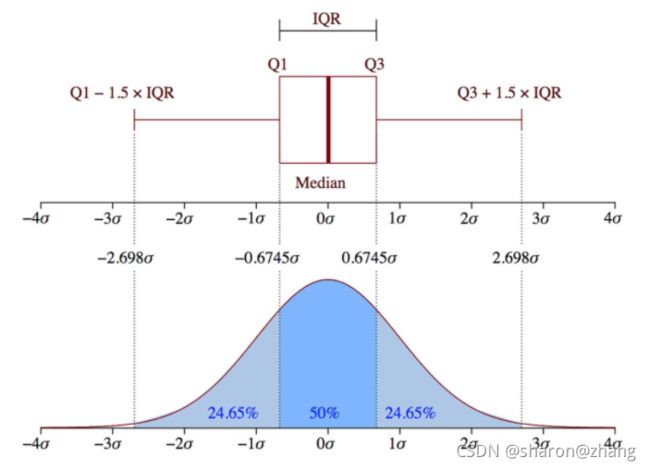
2.3 箱形图

四分位间距 (IQR) 的概念被用于构建箱形图。IQR 是统计学中的一个概念，通过将数据集分成四分位来衡量统计分散度和数据可变性。

简单来说，任何数据集或任意一组观测值都可以根据数据的值以及它们与整个数据集的比较情况被划分为四个确定的间隔。四分位数会将数据分为三个点和四个区间。

四分位间距对定义离群点非常重要。它是第三个四分位数和第一个四分位数的差 (IQR = Q3 -Q1)。在这种情况下，离群点被定义为低于箱形图下触须（或 Q1 − 1.5x IQR）或高于箱形图上触须（或 Q3 + 1.5x IQR）的观测值。

IQR是统计分散程度的一个度量，分散程度通过需要借助箱线图来观察，通常把小于 Q1 - 1.5 * IQR 或者大于 Q3 + 1.5 * IQR的数据点视作离群点，探测离群点的公式是：

outliers =  value < ( Q1 - 1.5 * IQR )  or value > ( Q3 + 1.5 * IQR )

这种探测离群点的方法，是箱线图默认的方法，箱线图提供了识别异常值/离群点的一个标准：

异常值通常被定义为小于 QL - l.5 IQR 或者 大于 Qu + 1.5 IQR的值，QL称为下四分位数， Qu称为上四分位数，IQR称为四分位数间距，是Qu上四分位数和QL下四分位数之差，其间包括了全部观察值的一半。

def detect_outliers(sr):
    q1 = sr.quantile(0.25)
    q3 = sr.quantile(0.75)
    iqr = q3-q1 #Interquartile range
    fence_low  = q1-1.5*iqr
    fence_high = q3+1.5*iqr
    outliers = sr.loc[(sr < fence_low) | (sr > fence_high)]
    return outliers

3、实战

上面数据基础知识的介绍了，下面我们进入今天的正题，也就是利用python与pandas进行数据分析，今天的主要目标就是找到数据中的异常值。（我们使用的是前面介绍的第一种方法）

3.1 加载数据

首先，我们需要加载进行分析的数据，同样使用beer的数据，不过这里的数据是经过处理的，可以看到abv属性列的值中大部分都是0.0*，基本都不超过1，但是也有数据是55，也就是说这些数据是远大于其他数据的，我们主要是对这部分数据进行处理。

class Repair_Dirty(object):
    __init_data = 0

    def __init__(self, filename):
        self.filename = filename

    def get_data(self):
        if self.filename == " ":
            # print("您输入的文件路径为空")
            return
        else:
            self.__init_data = pd.read_csv(self.filename)

        return self.__init_data

#主函数定义一个对象，并实现对方法的调用
if __name__ == "__main__":
    file_path = 'dirty_beer_last.csv'
    data_cla = Repair_Dirty(file_path)
    data = data_cla.get_data()#得到数据

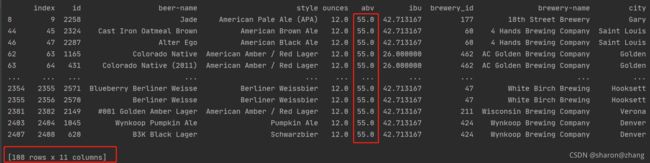
形如下面的数据图，红色框内数据为55的，就是我们所说的异常值，我们的目标就是通过第一种方法，将此类数据找出来。

3.2 检测异常值数据

使用第一种检测方式来检测异常值，我们主要是定义一个函数find_outlier()，并且函数是在类的内部实现的。

    # 找到异常值,abv列
    def find_outlier(self, attribute):
        data_att = self.__init_data[attribute]
        # 找到异常值
        outlier = data_att[np.abs(data_att - data_att.mean()) > 3 * data_att.std()]
        print(data.loc[data[attribute] == 55])#对abv属性的异常值进行输出
        #print(np.where(self.__init_data[attribute] == 55))  # 返回指定位置的索引
        return outlier

下面的图片中可以看到整个数据表中有108行数据中abv值为55的，所以很明显，我们基本上已经达到了想要的目标，找到了数据中的异常值，根据索引或者id我们便可以将其进行值替换操作，对异常值进行修复。

3.4 显示异常值的索引位置

既然已经找到了异常值，那我们再对其进行索引显示就比较简单了，也就是一行代码的事，其实在上面代码中也可以看到，只不过上面这行代码被我们给注释掉了，下面将其单独拿出来显示。

print(np.where(self.__init_data[attribute] == 55))  # 返回指定位置的索引

这行代码就是对异常值索引进行显示了。

至此，我们今天的数据分析异常值处理的博文就写到这里了，小张同学仍在马不停蹄的进行学习，希望这篇文章能够帮助正在学习数据分析的小伙伴！！！
奥利给

最后，将源代码附上，有需要的小伙伴可以自取。

import pandas as pd
import numpy as np
import re

class Repair_Dirty(object):
    __init_data = 0

    def __init__(self, filename):
        self.filename = filename

    def get_data(self):
        if self.filename == " ":
            # print("您输入的文件路径为空")
            return
        else:
            self.__init_data = pd.read_csv(self.filename)

        return self.__init_data
        
	# 找到异常值,abv列
    def find_outlier(self, attribute):
        data_att = self.__init_data[attribute]
        # 找到异常值
        outlier = data_att[np.abs(data_att - data_att.mean()) > 3 * data_att.std()]
        print(data.loc[data[attribute] == 55])#对abv属性的异常值进行输出
        print(np.where(self.__init_data[attribute] == 55))  # 返回指定位置的索引
        return outlier
        
if __name__ == "__main__":
    file_path = 'dirty_beer_last.csv'
    data_cla = Repair_Dirty(file_path)
    data = data_cla.get_data()
    print((data))
    if data is None:
        print("路径为空，程序退出！！！")
    else:
        data = data_cla.fill_na()
        outlier = data_cla.find_outlier()
        print(outlier)