Caputo 分数阶导数快速的 H2N2 插值逼近(附Matlab代码)
Caputo 分数阶导数快速的 H2N2 插值逼近
Caputo 分数阶导数的 H2N2 插值逼近 (附Matlab程序)
文章目录
- Caputo 分数阶导数快速的 H2N2 插值逼近
-
- H2N2 插值逼近格式推导
- 分数阶微分方程数值算例
-
- 数值算例
- 迭代格式
-
- 启动层(两层格式)
- 三层格式
- 数值结果
- 源代码
- 参考文献
H2N2 插值逼近格式推导
众所周知, 分数阶微分方程由于其存在全局依赖(非局部性)加大了求解困难, 于是有学者给出了一系列的快速算法,此处我们讨论 Caputo 分数阶导数基于 H2N2 逼近的快速算法, 其中分数阶导数的阶 γ ∈ ( 1 , 2 ) \gamma \in(1,2) γ∈(1,2).
本文中, 为简单起见, 省去了 N exp ( γ − 1 ) , s l ( γ − 1 ) , ω l ( γ − 1 ) N_{\exp }^{(\gamma-1)}, s_{l}^{(\gamma-1)}, \omega_{l}^{(\gamma-1)} Nexp(γ−1),sl(γ−1),ωl(γ−1) 中的上标 ( γ − 1 ) (\gamma-1) (γ−1). 应用引理 1.7.1 (见文末参考文献) 可得
0 C D t γ f ( t ) ∣ t = t n − 1 2 = 1 Γ ( 2 − γ ) [ ∫ t 0 t 1 2 f ′ ′ ( t ) ( t n − 1 2 − t ) 1 − γ d t + ∑ k = 1 n − 1 ∫ t k − 1 2 t k + 1 2 f ′ ′ ( t ) ( t n − 1 2 − t ) 1 − γ d t ] ≈ 1 Γ ( 2 − γ ) [ ∫ t 0 t 1 2 H 2 , 0 ′ ′ ( t ) ∑ l = 1 N exp ω l e − s l ( t n − 1 2 − t ) d t + ∑ k = 1 n − 2 ∫ t k − 1 2 t k + 1 2 N 2 , k ′ ′ ( t ) ∑ l = 1 N exp ω l e − s l ( t n − 1 2 − t ) d t + ∫ t n − 3 2 t n − 1 2 N 2 , n − 1 ′ ′ ( t ) ( t n − 1 2 − t ) 1 − γ d t ] = 1 Γ ( 2 − γ ) [ ∑ l = 1 N exp ω l F l n + δ t 2 f n − 1 ∫ t n − 3 2 t n − 1 2 2 ( t n − 1 2 − t ) 1 − γ d t ] ≡ F D ^ γ f ( t n − 1 2 ) , 2 ⩽ n ⩽ N , \begin{aligned} &\left.{ }_{0}^{C} D_{t}^{\gamma} f(t)\right|_{t=t_{n-\frac{1}{2}}} \\ =& \frac{1}{\Gamma(2-\gamma)}\left[\int_{t_{0}}^{t_{\frac{1}{2}}} f^{\prime \prime}(t)\left(t_{n-\frac{1}{2}}-t\right)^{1-\gamma} \mathrm{d} t+\sum_{k=1}^{n-1} \int_{t_{k-\frac{1}{2}}}^{t_{k+\frac{1}{2}}} f^{\prime \prime}(t)\left(t_{n-\frac{1}{2}}-t\right)^{1-\gamma} \mathrm{d} t\right] \\ \approx & \frac{1}{\Gamma(2-\gamma)}\left[\int_{t_{0}}^{t_{\frac{1}{2}}} H_{2,0}^{\prime \prime}(t) \sum_{l=1}^{N_{\text {exp }}} \omega_{l} \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t\right. &\left.+\sum_{k=1}^{n-2} \int_{t_{k-\frac{1}{2}}}^{t_{k+\frac{1}{2}}} N_{2, k}^{\prime \prime}(t) \sum_{l=1}^{N_{\text {exp }}} \omega_{l} \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t+\int_{t_{n-\frac{3}{2}}}^{t_{n-\frac{1}{2}}} N_{2, n-1}^{\prime \prime}(t)\left(t_{n-\frac{1}{2}}-t\right)^{1-\gamma} \mathrm{d} t\right] \\ =& \frac{1}{\Gamma(2-\gamma)}\left[\sum_{l=1}^{N_{\text {exp }}} \omega_{l} F_{l}^{n}+\delta_{t}^{2} f^{n-1} \int_{t_{n-\frac{3}{2}}}^{t_{n-\frac{1}{2}}^{2}}\left(t_{n-\frac{1}{2}}-t\right)^{1-\gamma} \mathrm{d} t\right] \\ \equiv &{ }^{\mathcal{F}} \hat{D}^{\gamma} f\left(t_{n-\frac{1}{2}}\right), \quad 2 \leqslant n \leqslant N, \end{aligned} =≈=≡0CDtγf(t)∣∣t=tn−21Γ(2−γ)1⎣⎡∫t0t21f′′(t)(tn−21−t)1−γdt+k=1∑n−1∫tk−21tk+21f′′(t)(tn−21−t)1−γdt⎦⎤Γ(2−γ)1⎣⎡∫t0t21H2,0′′(t)l=1∑Nexp ωle−sl(tn−21−t)dtΓ(2−γ)1⎣⎡l=1∑Nexp ωlFln+δt2fn−1∫tn−23tn−212(tn−21−t)1−γdt⎦⎤FD^γf(tn−21),2⩽n⩽N,+k=1∑n−2∫tk−21tk+21N2,k′′(t)l=1∑Nexp ωle−sl(tn−21−t)dt+∫tn−23tn−21N2,n−1′′(t)(tn−21−t)1−γdt⎦⎤
其中
F l n = ∫ t 0 t 1 2 H 2 , 0 ′ ′ ( t ) e − s l ( t n − 1 2 − t ) d t + ∑ k = 1 n − 2 ∫ t k − 1 2 t k + 1 2 N 2 , k ′ ′ ( t ) e − s l ( t n − 1 2 − t ) d t 1 ⩽ l ⩽ N exp , 2 ⩽ n ⩽ N \begin{aligned} F_{l}^{n}=\int_{t_{0}}^{t_{\frac{1}{2}}} H_{2,0}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t+& \sum_{k=1}^{n-2} \int_{t_{k-\frac{1}{2}}}^{t_{k+\frac{1}{2}}} N_{2, k}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t \\ & 1 \leqslant l \leqslant N_{\exp }, \quad 2 \leqslant n \leqslant N \end{aligned} Fln=∫t0t21H2,0′′(t)e−sl(tn−21−t)dt+k=1∑n−2∫tk−21tk+21N2,k′′(t)e−sl(tn−21−t)dt1⩽l⩽Nexp,2⩽n⩽N
利用如下递推算法计算 F l n F_{l}^{n} Fln :
F l n = ∫ t 0 t 1 2 H 2 , 0 ′ ′ ( t ) e − s l ( t n − 1 2 − t ) d t + ∑ k = 1 n − 2 ∫ t k − 1 2 t k + 1 2 N 2 , k ′ ′ ( t ) e − s l ( t n − 1 2 − t ) d t F_{l}^{n}=\int_{t_{0}}^{t_{\frac{1}{2}}} H_{2,0}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t+\sum_{k=1}^{n-2} \int_{t_{k-\frac{1}{2}}}^{t_{k+\frac{1}{2}}} N_{2, k}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t Fln=∫t0t21H2,0′′(t)e−sl(tn−21−t)dt+∑k=1n−2∫tk−21tk+21N2,k′′(t)e−sl(tn−21−t)dt
= e − s l τ [ ∫ t 0 t 1 H 2 , 0 ′ ′ ( t ) e − s l ( t n − 3 2 − t ) d t + ∑ k = 1 n − 3 ∫ t k − 1 2 t k + 1 2 N 2 , k ′ ′ ( t ) e − s l ( t n − 3 2 − t ) d t ] =\mathrm{e}^{-s_{l} \tau}\left[\int_{t_{0}}^{t_{1}} H_{2,0}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{3}{2}}-t\right)} \mathrm{d} t+\sum_{k=1}^{n-3} \int_{t_{k-\frac{1}{2}}}^{t_{k+\frac{1}{2}}} N_{2, k}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{3}{2}}-t\right)} \mathrm{d} t\right] =e−slτ[∫t0t1H2,0′′(t)e−sl(tn−23−t)dt+∑k=1n−3∫tk−21tk+21N2,k′′(t)e−sl(tn−23−t)dt]
+ ∫ t n − 5 2 t n − 3 2 N 2 , n − 2 ′ ′ ( t ) e − s l ( t n − 1 2 − t ) d t +\int_{t_{n-\frac{5}{2}}}^{t_{n-\frac{3}{2}}} N_{2, n-2}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t +∫tn−25tn−23N2,n−2′′(t)e−sl(tn−21−t)dt
= e − s l τ F l n − 1 + δ t 2 f n − 2 ∫ t n − 5 2 t n − 3 2 e − s l ( t n − 1 2 − t ) d t =\mathrm{e}^{-s_{l} \tau} F_{l}^{n-1}+\delta_{t}^{2} f^{n-2} \int_{t_{n-\frac{5}{2}}}^{t_{n-\frac{3}{2}}} \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t =e−slτFln−1+δt2fn−2∫tn−25tn−23e−sl(tn−21−t)dt
= e − s l τ F l n − 1 + B l ( δ t f n − 3 2 − δ t f n − 5 2 ) , 3 ⩽ n ⩽ N =\mathrm{e}^{-s_{l} \tau} F_{l}^{n-1}+B_{l}\left(\delta_{t} f^{n-\frac{3}{2}}-\delta_{t} f^{n-\frac{5}{2}}\right), \quad 3 \leqslant n \leqslant N =e−slτFln−1+Bl(δtfn−23−δtfn−25),3⩽n⩽N,
其中
F l 2 = ∫ t 0 t 1 2 H 2 , 0 ′ ′ ( t ) e − s l ( t 3 2 − t ) d t = 2 s l τ ( e − s l τ − e − 3 2 s l τ ) ( δ t f 1 2 − f ′ ( t 0 ) ) F_{l}^{2}=\int_{t_{0}}^{t_{\frac{1}{2}}} H_{2,0}^{\prime \prime}(t) \mathrm{e}^{-s_{l}\left(t_{\frac{3}{2}}-t\right)} \mathrm{d} t=\frac{2}{s_{l} \tau}\left(\mathrm{e}^{-s_{l} \tau}-\mathrm{e}^{-\frac{3}{2} s_{l} \tau}\right)\left(\delta_{t} f^{\frac{1}{2}}-f^{\prime}\left(t_{0}\right)\right) Fl2=∫t0t21H2,0′′(t)e−sl(t23−t)dt=slτ2(e−slτ−e−23slτ)(δtf21−f′(t0))
B l = 1 τ ∫ t n − 5 2 t n − 3 2 e − s l ( t n − 1 2 − t ) d t = 1 s l τ ( e − s l τ − e − 2 s l τ ) B_{l}=\frac{1}{\tau} \int_{t_{n-\frac{5}{2}}}^{t_{n-\frac{3}{2}}} \mathrm{e}^{-s_{l}\left(t_{n-\frac{1}{2}}-t\right)} \mathrm{d} t=\frac{1}{s_{l} \tau}\left(\mathrm{e}^{-s_{l} \tau}-\mathrm{e}^{-2 s_{l} \tau}\right) Bl=τ1∫tn−25tn−23e−sl(tn−21−t)dt=slτ1(e−slτ−e−2slτ)
综上得到计算 0 C D t γ f ( t ) ∣ t = t n − 1 2 { }_{0}^{C} D_{t}^{\gamma} f(t)\mid_{t=t_{n-\frac{1}{2}}} 0CDtγf(t)∣t=tn−21 的如下算法:
{ F D ^ γ f ( t n − 1 2 ) = 1 Γ ( 2 − γ ) [ ∑ l = 1 N exp ω l F l n + τ 2 − γ 2 − γ δ t 2 f n − 1 ] , 2 ⩽ n ⩽ N , F l 2 = 2 τ ∫ t 0 t 1 2 e − s l ( t 3 2 − t ) d t ( δ t f 1 2 − f ′ ( t 0 ) ) , 1 ⩽ l ⩽ N exp F l n = e − s l τ F l n − 1 + B l ( δ t f n − 3 2 − δ t f n − 5 2 ) , 1 ⩽ l ⩽ N exp , 3 ⩽ n ⩽ N . \left\{\begin{array}{l} {}^{F} \hat{D}^{\gamma} f\left(t_{n-\frac{1}{2}}\right)=\frac{1}{\Gamma(2-\gamma)}\left[\sum\limits_{l=1}^{N_{\exp }} \omega_{l} F_{l}^{n}+\frac{\tau^{2-\gamma}}{2-\gamma} \delta_{t}^{2} f^{n-1}\right], \quad 2 \leqslant n \leqslant N, \\ F_{l}^{2}=\frac{2}{\tau} \int_{t_{0}}^{t_{\frac{1}{2}}} \mathrm{e}^{-s_{l}\left(t_{\frac{3}{2}}-t\right)} \mathrm{d} t\left(\delta_{t} f^{\frac{1}{2}}-f^{\prime}\left(t_{0}\right)\right), \quad 1 \leqslant l \leqslant N_{\exp } \\ F_{l}^{n}=\mathrm{e}^{-s_{l} \tau} F_{l}^{n-1}+B_{l}\left(\delta_{t} f^{n-\frac{3}{2}}-\delta_{t} f^{n-\frac{5}{2}}\right), \quad 1 \leqslant l \leqslant N_{\exp }, 3 \leqslant n \leqslant N . \end{array}\right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧FD^γf(tn−21)=Γ(2−γ)1[l=1∑NexpωlFln+2−γτ2−γδt2fn−1],2⩽n⩽N,Fl2=τ2∫t0t21e−sl(t23−t)dt(δtf21−f′(t0)),1⩽l⩽NexpFln=e−slτFln−1+Bl(δtfn−23−δtfn−25),1⩽l⩽Nexp,3⩽n⩽N.
我们称上述公式为快速的 H2N2 逼近或快速的 H2N2 公式. 应用快速的 H2N2 公式可以对时间分数阶波方程建立 3 − γ 3-\gamma 3−γ 阶时间精度的差分格式.
分数阶微分方程数值算例
数值算例
求解初值问题
{ 0 C D t γ u ( t ) = f ( t ) , 0 < t ⩽ T u ( 0 ) = 0 , u ′ ( 0 ) = 0 \left\{\begin{array}{l} { }_{0}^{C} \mathbf{D}_{t}^{\gamma} u(t)=f(t), \quad 0
其中 γ ∈ ( 1 , 2 ) \gamma \in(1,2) γ∈(1,2), f ( t ) = 6 Γ ( 2 − γ ) ( 1 2 − γ − 1 3 − γ ) t 3 − γ . f(t)=\frac{6}{\Gamma(2-\gamma)}(\frac{1}{2-\gamma}-\frac{1}{3-\gamma})t^{3-\gamma}. f(t)=Γ(2−γ)6(2−γ1−3−γ1)t3−γ.
该方程精确解为 u ( t ) = t 3 . u(t)=t^3. u(t)=t3.
迭代格式
将数值算例结合 H2N2 逼近公式可得到如下迭代格式.
启动层(两层格式)
由于启动层不存在明显全局依赖, 故直接采用如下的传统 H2N2 格式求解即可.
1 Γ ( 2 − γ ) [ b ^ 0 ( 1 , γ ) ⋅ u 1 − u 0 τ − b ^ 0 ( 1 , γ ) u ′ ( t 0 ) ] = f ( t 1 ) \frac{1}{\Gamma(2-\gamma)}\left[\hat{b}_{0}^{(1, \gamma)} \cdot \frac{u^{1}-u^{0}}{\tau}-\hat{b}_{0}^{(1, \gamma)} u^{\prime}\left(t_{0}\right)\right]=f\left(t_{1}\right) Γ(2−γ)1[b^0(1,γ)⋅τu1−u0−b^0(1,γ)u′(t0)]=f(t1)
b 0 ( 1 , γ ) ^ ⋅ u 1 − u 0 τ − b ^ 0 ( 1 , γ ) u ′ ( t 0 ) = f ( t 1 ) ⋅ Γ ( 2 − r ) \hat{b_{0}^{(1, \gamma)}} \cdot \frac{u^{1}-u^{0}}{\tau}-\hat{b}_{0}^{(1, \gamma)} u^{\prime}\left(t_{0}\right)=f\left(t_{1}\right) \cdot\Gamma(2-r) b0(1,γ)^⋅τu1−u0−b^0(1,γ)u′(t0)=f(t1)⋅Γ(2−r)
得到启动层:
u ( t 1 ) = τ ⋅ Γ ( 2 − r ) b ^ 0 ( 1 , γ ) ⋅ f ( t 1 ) + τ b ^ 0 ( 1 , γ ) u ′ ( t 0 ) + u ( t 0 ) . u\left(t_{1}\right) =\frac{\tau \cdot\Gamma(2-r)}{\hat{b}_{0}^{(1, \gamma)}} \cdot f\left(t_{1}\right)+\tau \hat{b}_{0}^{(1, \gamma)} u^{\prime}\left(t_{0}\right)+u\left(t_{0}\right) . u(t1)=b^0(1,γ)τ⋅Γ(2−r)⋅f(t1)+τb^0(1,γ)u′(t0)+u(t0).
三层格式
1 Γ ( 2 − γ ) [ ∑ l = 1 N exp ω l F l n + τ 2 − γ 2 − γ ( 1 τ 2 u n − 2 τ 2 u n − 1 + 1 τ 2 u n − 2 ) = f ( t n − 1 2 ) \frac{1}{\Gamma(2-\gamma)}\left[\sum\limits_{l=1}^{N_{\text {exp }}} \omega_{l} F_{l}^{n}+\frac{\tau^{2-\gamma}}{2-\gamma}\left(\frac{1}{\tau^{2}} u^{n}-\frac{2}{\tau^{2}} u^{n-1}+\frac{1}{\tau^{2}} u^{n-2}\right)=f\left(t_{n-\frac{1}{2}}\right)\right. Γ(2−γ)1⎣⎡l=1∑Nexp ωlFln+2−γτ2−γ(τ21un−τ22un−1+τ21un−2)=f(tn−21)
得到三层迭代格式:
u ( t n ) = Γ ( 3 − γ ) ⋅ τ γ ⋅ f ( t n − 1 2 ) − ( 2 − γ ) τ γ ∑ i = 1 N e x p ω l F l n + 2 u ( t n − 1 ) − u ( t n − 2 ) u\left(t_{n}\right)=\Gamma(3-\gamma) \cdot \tau^{\gamma} \cdot f\left(t_{n-\frac{1}{2}}\right)-(2 - \gamma) \tau^{\gamma} \sum\limits_{i=1}^{N_{e x p}} \omega_{l} F_{l}^{n}+2 u\left(t_{n-1}\right)-u\left(t_{n-2}\right) u(tn)=Γ(3−γ)⋅τγ⋅f(tn−21)−(2−γ)τγi=1∑NexpωlFln+2u(tn−1)−u(tn−2)
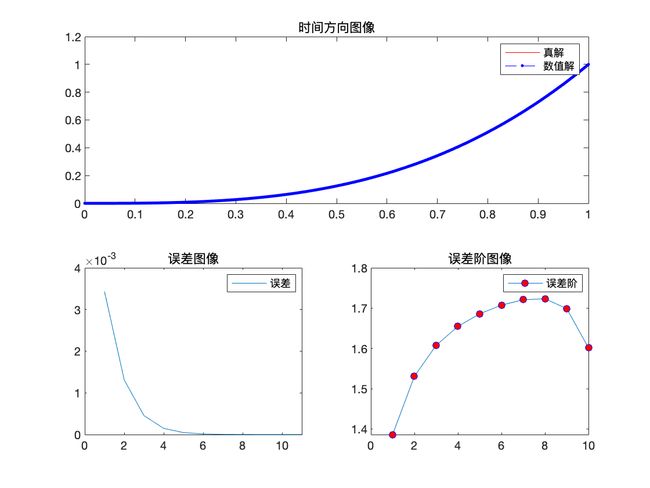
数值结果
程序运行时间:
时间步长为 0.000100 时快速 H2N2 插值逼近历时 0.751304 秒.
而相同的网格剖分及精度下, 传统的 H2N2 插值逼近需历时 57.789599 秒.
源代码
主程序:
clc,clear
tic
%% 初始化定解问题
alpha=1.2;
epsilon=1e-8;
tau_hat=1e-6;
tau=1/10000; % @tau 时间步长
T_a=0; % @T 时间求解区域
T_b=1;
N=(T_b-T_a)/tau; % @N t被分割的区间数
t=T_a:tau:T_b; % @t 时间向量
u=zeros(1,N+1); % @u 初始化数值解
u(1)=f_ic(t(1),0); % 定义初值条件
[xs,ws,nexp] = sumofexpappr2new(alpha-1,epsilon,tau_hat,T_b);
%% 两层格式(启动层)
n=2;
m=n-1;
% 求解迭代系统(由0层求第1层的值)
u(n)=tau*gamma(2-alpha)/b_hat(0,m,alpha,tau)*f_source((t(2)+t(1))/2,alpha)...
+tau*b_hat(0,m,alpha,tau)*f_ic(t(1),1)...
+u(n-1);
fprintf('进程:\t%d/%d\n',n,N+1)
%% 三层格式
F_l=2./(xs*tau).*(exp(1).^(-xs*tau)-exp(1).^(-3/2*xs*tau)).*(1/tau*(u(2)-u(1))-f_ic(t(1),1));
B_l=1./(xs*tau).*(exp(1).^(-xs*tau)-exp(1).^(-2*xs*tau));
for n=3:N+1
% 求解迭代系统(由 k-2 层及第 k-1 层求第 k 层的值)
u(n)=gamma(3-alpha)*tau^alpha*f_source((t(n)+t(n-1))/2,alpha)...
-(2-alpha)*tau^alpha*(ws'*F_l)...
+2*u(n-1)-u(n-2);
F_l=exp(1).^(-xs*tau).*F_l+B_l.*(1/tau*(u(n)-2*u(n-1)+u(n-2)));
fprintf('进程:\t%d/%d\n',n,N+1)
end
clc
fprintf('时间步长为 %f 时快速 H2N2 插值逼近 %d\n',tau)
toc
%% 误差分析
U=zeros(size(u));
for n=1:N+1
U(n)=u_exact(t(n),0);
end
Error=max(max(abs(u-U)))
%% 绘图
% figure
% plot(t,u)
% hold on
% plot(t,U)
% legend('数值解','精确解')
此处由于字数限制, 仅展示了主程序代码部分, 若需要绘图及误差分析等完整代码, 请在评论区留下邮箱.
参考文献
孙志忠,高广花.分数阶微分方程的有限差分方法(第二版).北京:科学出版社,2021.
本人水平有限, 若有不妥之处, 恳请批评指正.
作者:图灵的猫
作者邮箱: [email protected]