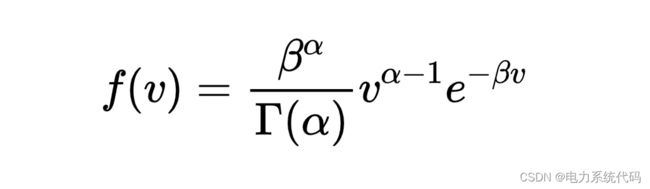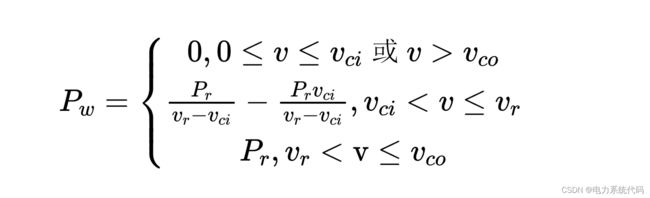基于蒙特卡诺的风、光模型出力（Matlab代码实现）
目录
1 概述
2 光伏DG出力概率模型
2.1 光照强度分布特性
2.2 光伏DG有功出力
3 风电DG出力概率模型
3.1 风速分布特性
3.2 风电 DG有功出力
4 Matlab实现
1 概述
(1)规模化新能源挤占通道,消纳能力与利用率相互制约。
大规模新能源并网,新能源电力、电量占比不断提高,消纳与利用率矛盾突出:与常规机组相互挤占通道,重要断面满功率运行压力较大;风电反调峰特性突出,加剧电网调峰困难,消纳与利用率相互制约,保证消纳水平的基础上,利用率存在下降的趋势。在大型风电场附近如果有500kV特高压输电线路,这个风电场风电利用率可以基本可以达到接近100% ,可以通过特高压线路输送到远方;如果没有特高压线路,只能就近消纳。还有新能源只能发有功,由于功角因素,有时潮流不是按照我们想要的方向流入,如部分流到其它地区啦,需要在-些地方加装大型无功装置,形成一 个“截面” ,不让新能源流过去。
(2)新能源出力不可控因素较多,电力平衡不确定性较大。
风光新能源出力受夭气、气候影响巨大,短期、中长期电力供应均处于难预测状态。受风向、风力、光照强度等影响,风光出力具有随机性、波动性、间歇性等特点,新能源日内出力波折;寒潮或连晴高温等极端气候下,电力需求陡增,但新能源最小出力可能处于较低水平，平衡支 撑能力不足。
(3)系统等效转动惯量下降,频率调节和稳定问题凸显
新能源并网规模、出幼占比不断提高,常规机组被大量电力电子设备替代,系统旋转惯量持续减小,频率调节能力严重下降,电网存在频率越限甚至稳定破坏风险。
2019年8月,英国伦敦发生大停电事故，损失负荷约93万千瓦,约100万人受到停电影响。这是自2003年伦敦大停电”以来，英国发生的规模最大、影响人口最多的停电事故!经分析,事故原因在于风电新能源装机容量占比达到34.71%，系统等效转动惯量不足,系统频率在机组连续脱网后陡降至49Hz以吓,低频减载动作,切除5%负荷导致的停电。
(4)无功支撑能力下降，电压控制和稳定问题突出
一方面新能源调压能力不足 ，大规模新能源并网地区电压控制困难另一方面高比例受电地区动态无功支撑能力不足,系统电压调节能力持续下降，系统安全面临电压失稳风险。
直流与新能源机组不具备常规电源的动态无功支撑能力,随着受端直流大量馈入,新能源比快
速提高,系统动态无功储备急剧下降。特高压直流故障诱发电压稳定问题,对于送端电网表现为过电压;对于受端电网表现为持续低压甚电压崩溃,系统面临大面积停电风险。
(5)跨区交直流耦合故障全局化,存在非I频稳定性问题
随着新能源并网规模的扩大以及特高压交直流互联网的快速发展,在扰动事件冲击下,系统的能量吸放特性更为复杂，呈现出新的形态。
送、受端电网通过交直流紧密耦合,电网.一体化特征显著,跨区交直流动态交互特性更加复杂，局部的暂态能量冲击易引发全局的稳定性问题。新能源大规模并网,电源结构深度调整电网稳定形态更加复杂,电力电子装置的快速响应特性引发非I频的稳定性问题。
2 光伏DG出力概率模型
2.1 光照强度分布特性
光伏发电机组产生的有功功率通常取决于光伏发电机组所在位置的光强。为了获得更精确的概率分布特性,采用有效的方法对测量的光强数据进行拟合是非常重要的。
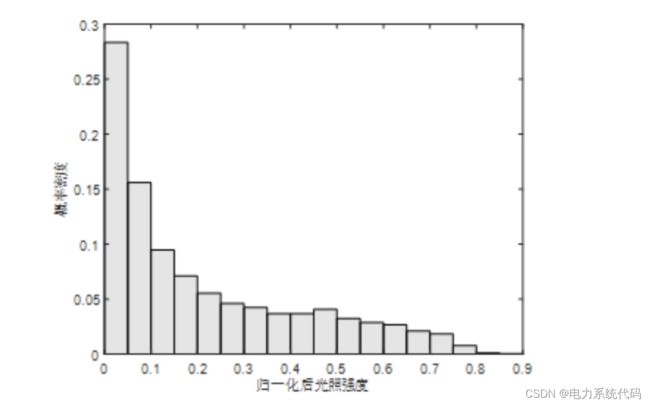
上图为某光伏电站全年7:00-18:00实测光照强度数据，从图中可以看出风速的确存在一定的分布特性，所以本文采用Beta分布，Normal分布，同实测光照强度数据进行拟合。
(1)Beta分布
概率密度函数:
式中:
为光照强度
，
为Gamma函数，
为最大光照强度，
、
为Beta分布的参数。参数的确定由实际数据进行拟合得到。
( 2)Normal分布
概率密度函数:
式中: 为光照强度
， 
、
为 Normal分布的参数。参数的确定由实际数据进行拟合得到。
2.2 光伏DG有功出力
光伏功率 = Beta分布 * 最大光强 * 组件总面积 * 光电转换率
% 光伏有功出力样本
pv_samp(1,:)=betarnd(a_pv,b_pv,1,times);%生成形状为(1,times,)，参数为a_pv,b_pv的Beta分布
Ppv_samp(1,:)=pv_samp(1,:)*rmax*S_pv*prey_pv;% 光伏功率=Beta分布*最大光强*组件总面积*光电转换率3 风电DG出力概率模型
3.1 风速分布特性
风电机组发出的有功功率与机组所在位置的风速大小。针对实测的风速数据用有效的方法去拟合来获得较为精确的概率分布特性,意义显得尤为重要。
上图为风力发电站的年实测风速数据。从图中可以看出,风速具有一定的分布特征:偏态分布。本文采用Weibull分布、Rayleigh分布和Gamma分布对实测风速数据进行拟合。
(1)Gamma分布
概率密度函数:
式中: 
为风速(m/s)，为Gamma 函数，α、β为Gamma分布的参数。参数的确定由实际数据进行拟合得到。
本文采用Gamma分布，当然也可以换成下面两个分布。
wt_samp =gamrnd(c_wt,k_wt,1,times); % 风速 产生服从gammer分布的样本 ，形状为（(1,times,)
%wt_samp =wblrnd(c_wt,k_wt,1,times); % 风速 可以修改为服从weibull分布的样本 ，形状为（(1,times,)(2)Rayleigh分布
概率密度函数:
式中:为风速(m/s)，为 Rayleigh分布的参数。参数的确定由实际数据进行拟合得到。
Rayleigh分布属于weibull分布的一个特例，通常适用于长时间（一年）及其以上风速统计数据，拟合的结果与实际的结果有10%的误差。
(3)Weibull分布
概率密度函数:
式中:为风速(m/s)，
、
为 Weibull,分布的两个参数。参数的确定由实际数据进行拟合得到。
weibull分布应用广泛，形式简单，计算简单，但其缺点是不能适应某些地区极端天气的风速分布。
3.2 风电 DG有功出力
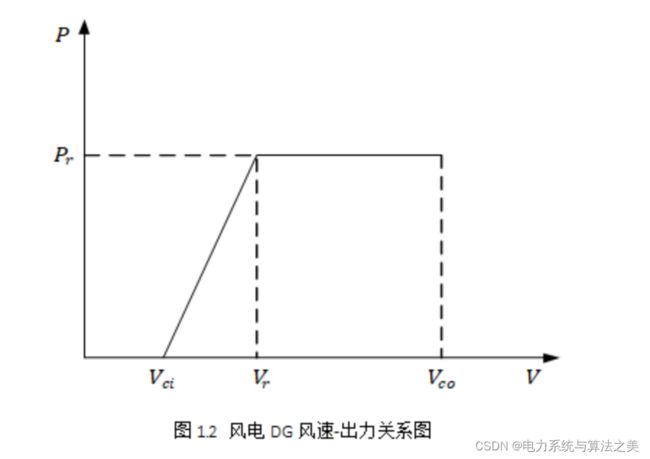
在得到风速模型后，需要得到风力机出力和风速的公式:
式中:为风速，
为切入风速，
为切出风速,
,为风电机组额定风速，
为风电机组的额定输出功率。
4 Matlab实现
本文只展示部分代码，全部代码点这里：正在为您运送作品详情
%% 风机出力
for i=1:times %得到风电出力样本
if wt_samp(i)vci&&wt_samp(i)PN_wt %如果风电功率大于额定功率
Pwt_samp(i)=PN_wt; %则风电功率等于额定功率
end
end
if wt_samp(i)>vN&&wt_samp(i)< vco %如果风速大于额定风速 同时小于切出风速
Pwt_samp(i)=PN_wt;%风电功率等于额定功率
end
if wt_samp(i)> vco %如果风速大于切出风速
Pwt_samp(i)=0;%风电功率等于0
end
end