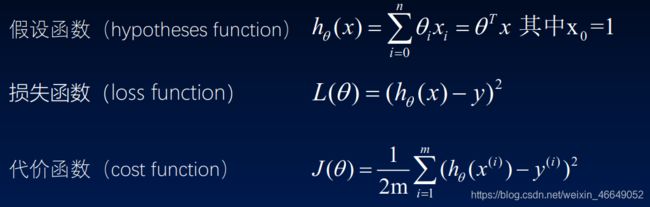机器学习1-线性回归、Ridge回归、LASSO回归
文章目录
-
-
- 1.形式化定义
- 2.梯度下降法
-
- 1)举例
- 2)数学原理
- 3)代码演示
- 3.梯度下降法求解线性回归
-
- 1)理论
- 2)线性回归代码实现梯度下降算法
- 4.梯度下降算法的变形
- 5.模型评价指标
-
- 1)理论
- 2)模型评价指标代码
- 6.欠拟合与过拟合与正则化
- 7.岭回归求解与代码实现
- 8.LASSO回归推导过程、求解举例说明及其代码实现
-
- 1)推导过程
- 2)求解举例说明
- 3)代码实现
- 9. 最小二乘法求线性回归
-
- 1)理论部分
- 2)最小二乘法求解线性回归代码实现
- 10.使用sklearn实现线性回归、Ridge、 LASSO 、ElasyicNet
-
- 1)Scikit learn介绍
- 2)sklearn代码实现
- 11.案例:波士顿房价预测
-
- 1)机器学习项目流程
- 2)代码实现
-
1.形式化定义
2.梯度下降法
1)举例
2)数学原理
3)代码演示
# 梯度下降法代码实现
import matplotlib.pyplot as plt
# 梯度下降法代码实现
import numpy as np
x = np.linspace(-6, 4, 100)
y = x ** 2 + 2 * x + 5
# 构建绘图窗口与坐标
fig, ax = plt.subplots()
ax.plot(x, y, linewidth=3)
plt.show()
# 初始化x,步长α和迭代次数
# 步长要控制,不宜过大
# 可以通过设置精度来控制迭代次数
x = 3
alpha = 0.8
iteraterNum = 10
# y的导数为2x-2,迭代求theta
for i in range(iteraterNum):
x = x - alpha * (2 * x + 2)
print(x)
-0.9758135295999999
3.梯度下降法求解线性回归
1)理论
2)线性回归代码实现梯度下降算法
# 线性回归代码实现梯度下降算法
import matplotlib.pyplot as plt
import numpy as np
# 定义一个加载数据的函数
def loaddata():
data = np.loadtxt('data1.txt', delimiter=',')
n = data.shape[1] - 1 # 特征数
X = data[:, 0:n]
# reshape(-1,1)表示转变成一行
y = data[:, 1].reshape(-1, 1)
return X, y
# 定义特征标准化函数-减小异常点的影响
# 标准化方式是:对每一个特征,这列中的每个数据分别减去这列的均值,然后再除以这列的方差
def featureNormalize(X):
# 均值
mu = np.average(X, axis=0)
# 方差
# 参数ddof=1,表示求方差时除的n-1,否则的话,除以n
sigma = np.std(X, axis=0, ddof=1)
X = (X - mu) / sigma
return X, mu, sigma
# 定义计算代价函数
def computeCost(X, y, theta):
m = X.shape[0] # 数据量
# np.dot()这里均为一维向量,向量点乘
# np.power(x1,x2)表示对x1中的每个元素求x2次方
return np.sum(np.power(np.dot(X, theta) - y, 2)) / (2 * m)
# 定义梯度下降求解函数
def gradientDescent(X, y, theta, iterations, alpha):
# transpose()转置
c = np.ones(X.shape[0]).transpose()
# 对原始数据加入一个全为1的列,插入
X = np.insert(X, 0, values=c, axis=1)
m = X.shape[0] # 数据量
n = X.shape[1] # 特征数
costs = np.zeros(iterations)
for num in range(iterations):
for j in range(n):
theta[j] = theta[j] + (alpha / m) * np.sum((y - np.dot(X, theta)) * X[:, j].reshape(-1, 1))
costs[num] = computeCost(X, y, theta)
return theta, costs
# 预测函数-预测值
def predict(X):
X = (X - mu) / sigma
c = np.ones(X.shape[0]).transpose()
X = np.insert(X, 0, values=c, axis=1)
return np.dot(X, theta)
# 定义评价函数mse
def mse(y_true, y_pred):
return (1 / len(y_true)) * np.sum(np.power(y_true - y_pred, 2))
if __name__ == '__main__':
# 加载数据
X_orgin, y = loaddata()
# 标准化
X, mu, sigma = featureNormalize(X_orgin)
theta = np.zeros(X.shape[1] + 1).reshape(-1, 1)
iterations = 400
alpha = 0.01
# 梯度下降求解
theta, costs = gradientDescent(X, y, theta, iterations, alpha)
print(theta)
# 预测值
print(predict([[5.734]]))
# 模型的评价
model_pred = predict(X_orgin)
print(model_pred)
print('mse',mse(y,model_pred))
# mse 8.972317211137899
# 画子图
ax1 = plt.subplot(121)
ax2 = plt.subplot(122)
# 画函数损失图
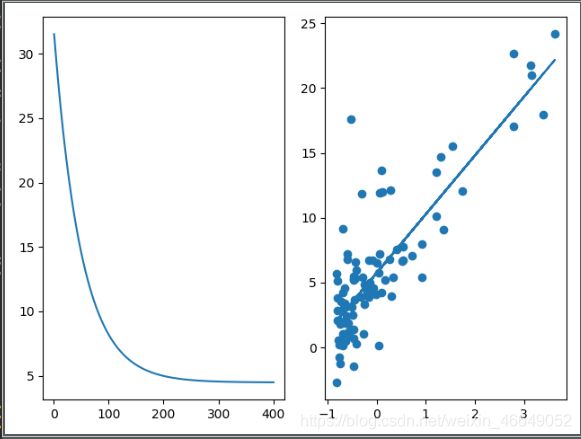
x_axis = np.linspace(1, iterations, iterations)
ax1.plot(x_axis, costs[0:iterations])
# 画数据散点图与直线
ax2.scatter(X, y)
h_theta = theta[0] + theta[1] * X
ax2.plot(X, h_theta)
plt.show()
[[5.73431935]
[4.53050051]]
[[2.89441782]]
4.梯度下降算法的变形
批量梯度下降:
每次theta的更新,需要使用全部数据样本,耗时
随机梯度下降:
每一次theta更新,只使用一个样本,减少了计算量
小批量梯度下降:推荐
介于批量梯度下降与随机梯度下降的折中,每一次使用batch_size个样本进行更新,较少计算量
将样本随机打乱,每一次使用batch_size个样本进行更新,进行梯度下降的次数m/batch_size
5.模型评价指标
1)理论
2)模型评价指标代码
# 常见模型评价指标
# 1.均方误差
import numpy as np
y_true = np.array([1, 2, 3, 4, 5])
y_pred = np.array([1.1, 2.2, 3.1, 4.2, 5])
# 定义函数
def mse(y_true, y_pred):
return (1 / len(y_true)) * np.sum(np.power(y_true - y_pred, 2))
print(mse(y_true, y_pred)) # 0.020000000000000035
# 2.均方根误差
# 定义函数
def rmse(y_true, y_pred):
# np.sqrt表示开根号
return np.sqrt((1 / len(y_true)) * np.sum(np.power(y_true - y_pred, 2)))
print(rmse(y_true, y_pred)) # 0.14142135623730964
# 3.平均绝对误差
# 定义函数
def mae(y_true, y_pred):
# np.abs表示绝对值
return np.sum(np.abs(y_true - y_pred)) / len(y_true)
print(mae(y_true, y_pred)) # 0.1200000000000001
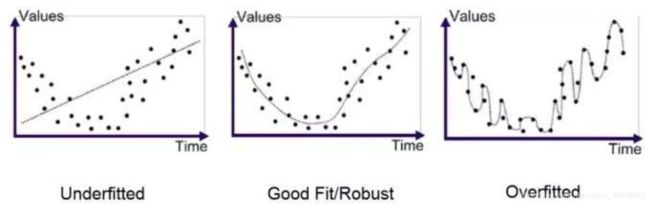
6.欠拟合与过拟合与正则化
7.岭回归求解与代码实现
# 岭回归求解
import matplotlib.pyplot as plt
import numpy as np
# 定义一个加载数据的函数
def loaddata():
data = np.loadtxt('data1.txt', delimiter=',')
n = data.shape[1] - 1 # 特征数
X = data[:, 0:n]
# reshape(-1,1)表示转变成一行
y = data[:, 1].reshape(-1, 1)
return X, y
# 定义特征标准化函数-减小异常点的影响
# 标准化方式是:对每一个特征,这列中的每个数据分别减去这列的均值,然后再除以这列的方差
def featureNormalize(X):
# 均值
mu = np.average(X, axis=0)
# 方差
# 参数ddof=1,表示求方差时除的n-1,否则的话,除以n
sigma = np.std(X, axis=0, ddof=1)
X = (X - mu) / sigma
return X, mu, sigma
# 定义计算代价函数
def computeCost(X, y, theta, lamda=0.001):
m = X.shape[0] # 数据量
# np.dot()这里均为一维向量,向量点乘
# np.power(x1,x2)表示对x1中的每个元素求x2次方
return np.sum(np.power(np.dot(X, theta) - y, 2)) / (2 * m) + np.sum(np.power(theta, 2)) * lamda
# 定义梯度下降求解函数
def gradientDescent(X, y, theta, iterations, alpha, lamda=0.001):
# transpose()转置
c = np.ones(X.shape[0]).transpose()
# 对原始数据加入一个全为1的列,插入
X = np.insert(X, 0, values=c, axis=1)
m = X.shape[0] # 数据量
n = X.shape[1] # 特征数
costs = np.zeros(iterations)
for num in range(iterations):
for j in range(n):
theta[j] = theta[j] + (alpha / m) * np.sum((y - np.dot(X, theta)) * X[:, j].reshape(-1, 1)) - 2 * lamda * \
theta[j]
costs[num] = computeCost(X, y, theta)
return theta, costs
# 预测函数-预测值
def predict(X):
X = (X - mu) / sigma
c = np.ones(X.shape[0]).transpose()
X = np.insert(X, 0, values=c, axis=1)
return np.dot(X, theta)
# 定义评价函数mse
def mse(y_true, y_pred):
return (1 / len(y_true)) * np.sum(np.power(y_true - y_pred, 2))
if __name__ == '__main__':
# 加载数据
X_orgin, y = loaddata()
# 标准化
X, mu, sigma = featureNormalize(X_orgin)
theta = np.zeros(X.shape[1] + 1).reshape(-1, 1)
iterations = 400
alpha = 0.01
# 梯度下降求解
theta, costs = gradientDescent(X, y, theta, iterations, alpha)
print(theta)
# 模型的评价
model_pred = predict(X_orgin)
# print(model_pred)
print('mse', mse(y, model_pred))
# mse 8.972317211137899
# 画子图
ax1 = plt.subplot(121)
ax2 = plt.subplot(122)
# 画函数损失图
x_axis = np.linspace(1, iterations, iterations)
ax1.plot(x_axis, costs[0:iterations])
# 画数据散点图与直线
ax2.scatter(X, y)
h_theta = theta[0] + theta[1] * X
ax2.plot(X, h_theta)
plt.show()
[[4.82704628]
[3.80873725]]
mse 10.624662198742348
8.LASSO回归推导过程、求解举例说明及其代码实现
1)推导过程
2)求解举例说明
3)代码实现
# LASSO回归代码实现
import matplotlib.pyplot as plt
import numpy as np
# 定义一个加载数据的函数
def loaddata():
data = np.loadtxt('data1.txt', delimiter=',')
n = data.shape[1] - 1 # 特征数
X = data[:, 0:n]
# reshape(-1,1)表示转变成一行
y = data[:, 1].reshape(-1, 1)
return X, y
# 定义特征标准化函数-减小异常点的影响
# 标准化方式是:对每一个特征,这列中的每个数据分别减去这列的均值,然后再除以这列的方差
def featureNormalize(X):
# 均值
mu = np.average(X, axis=0)
# 方差
# 参数ddof=1,表示求方差时除的n-1,否则的话,除以n
sigma = np.std(X, axis=0, ddof=1)
X = (X - mu) / sigma
return X, mu, sigma
# LASSO回归实现梯度下降法
def lasso_regression(X, y, iterations, lambd=0.2):
m, n = X.shape
# np.matric()表示矩阵
theta = np.matrix(np.zeros((n, 1)))
for it in range(iterations):
for k in range(n): # n个特征
# 计算常量值z_k和p_k
z_k = np.sum(X[:, k] ** 2)
p_k = 0
for i in range(m):
# 开始,根据公式计算p_k
p_k += X[i, k] * (y[i, 0] - np.sum([X[i, j] * theta[j, 0] for j in range(n) if j != k]))
# 结束
# w_k是一个临时变量,根据p_k的不同取值进行计算
if p_k < -lambd / 2:
w_k = (p_k + lambd / 2) / z_k
elif p_k > lambd / 2:
w_k = (p_k - lambd / 2) / z_k
else:
w_k = 0
theta[k, 0] = w_k
return theta
if __name__ == '__main__':
# 加载数据
X_orgin, y = loaddata()
# 标准化
X, mu, sigma = featureNormalize(X_orgin)
# 插入一列值为1的数据
X_1 = np.insert(X, 0, values=1, axis=1)
iterations = 400
theta = lasso_regression(X_1, y, iterations)
print(theta)
# 画数据散点图与直线
fig, ax = plt.subplots()
ax.scatter(X, y)
line = theta[0, 0] + theta[1, 0] * X
ax.plot(X, line)
plt.show()
[[5.83810412]
[4.61585958]]
9. 最小二乘法求线性回归
1)理论部分
详细过程见西瓜书多元线性回归推导部分
2)最小二乘法求解线性回归代码实现
# 最小二乘法求解线性回归
import matplotlib.pyplot as plt
import numpy as np
# 定义一个加载数据的函数
def loaddata():
data = np.loadtxt('data1.txt', delimiter=',')
n = data.shape[1] - 1 # 特征数
X = data[:, 0:n]
# reshape(-1,1)表示转变成一行
y = data[:, 1].reshape(-1, 1)
return X, y
if __name__ == '__main__':
X_orgin, y = loaddata()
# 插入一列值为1的数据
X = np.insert(X_orgin, 0, values=1, axis=1)
# 利用最小二乘法定义theta
# 数据量很大时,求逆效率很低;此时,可以考虑使用梯度下降法
# theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
# 如果逆矩阵不存在时,如下定义
lamda = 0.5
theta = np.linalg.inv(X.T.dot(X) + lamda * (np.matrix(np.identity(X.shape[1])))).dot(X.T).dot(y)
print(theta)
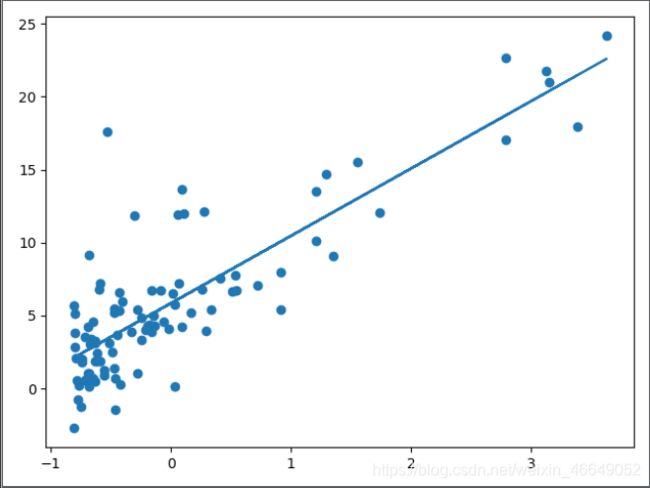
# 画出数据散点图与直线图
fig, ax = plt.subplots()
ax.scatter(X_orgin, y)
h_theta = theta[0] + theta[1] * X_orgin
ax.plot(X_orgin, h_theta, 'r', linewidth=2)
plt.show()
10.使用sklearn实现线性回归、Ridge、 LASSO 、ElasyicNet
1)Scikit learn介绍
2)sklearn代码实现
# 使用sklearn实现Ridge LASSO ElasyicNet
import numpy as np
import matplotlib.pyplot as plt
# LinearRegression线性回归(最小二乘法实现)
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
# 定义一个加载数据的函数
def loaddata():
data = np.loadtxt('data1.txt', delimiter=',')
n = data.shape[1] - 1 # 特征数
X = data[:, 0:n]
# reshape(-1,1)表示转变成一行
y = data[:, 1].reshape(-1, 1)
return X, y
if __name__ == '__main__':
X, y = loaddata()
# 线性回归(最小二乘实现)
model1 = LinearRegression()
# 加载数据并进行训练
model1.fit(X, y)
# intercept_属性可以输出 0 的值,coef_属性可以输出 1 到 的值
# 输出系数
print(model1.coef_)
# 输出截距
print(model1.intercept_)
# 岭回归
# alpha相当于lamda,表示正则化强度
# normalize设置为True表示对训练数据进行标准化
model2 = Ridge(alpha=0.01, normalize=True)
model2.fit(X, y)
# 输出系数
print(model2.coef_)
# 输出截距
print(model2.intercept_)
# LASSO回归
# alpha相当于lamda,表示正则化强度
# normalize设置为True表示对训练数据进行标准化
model3 = Lasso(alpha=0.01, normalize=True)
model3.fit(X, y)
# 输出系数
print(model3.coef_)
# 输出截距
print(model3.intercept_)
# ElasticNet回归
# alpha相当于lamda,表示正则化强度
# normalize设置为True表示对训练数据进行标准化
# l1_ratio表示L1与L2的占比
model4 = ElasticNet(alpha=0.01, l1_ratio=0.9, normalize=True)
model4.fit(X, y)
# 输出系数
print(model4.coef_)
# 输出截距
print(model4.intercept_)
# 画四个子图
ax1 = plt.subplot(221)
ax2 = plt.subplot(222)
ax3 = plt.subplot(223)
ax4 = plt.subplot(224)
ax1.scatter(X,y)
y_predict_1 = model1.predict(X)
ax1.plot(X,y_predict_1,'r')
ax2.scatter(X, y)
y_predict_2 = model2.predict(X)
ax2.plot(X, y_predict_2,'r')
ax3.scatter(X, y)
y_predict_3 = model3.predict(X)
ax3.plot(X, y_predict_3,'r')
ax4.scatter(X, y)
y_predict_4 = model4.predict(X)
ax4.plot(X, y_predict_4,'r')
plt.show()
[[1.19303364]]
[-3.89578088]
[[1.18122143]]
[-3.79939557]
[1.16745142]
[-3.68703508]
[1.06655392]
[-2.8637316]
11.案例:波士顿房价预测
1)机器学习项目流程
1获取数据
2数据预处理(数据清洗)
3数据分析与可视化
4选择合适的机器学习模型
5训练模型(使用交叉验证选择合适的参数)
6评价模型
7上线部署使用模型
2)代码实现
数据预处理(数据清洗)
我们获取的数据有可能存在下面的一些情况:
缺少数据值
含有错误的数据值,如年龄=200
数据不一致,等级编码有的是“1,2,3”有的却是“A,B,C ”
重复的记录值
数据集的分割
训练集:训练模型
验证集:选择合适的参数
测试集:测试模型的泛化能力
训练集与验证集-交叉验证
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
# 模型保存
import joblib
# 获取数据
boston = load_boston()
# 数据集的描述
# print(boston.DESCR)
# 特征X与标签y
X = boston.data
y = boston.target
# # pandas方法读取数据
# data = pd.read_csv('boston.xls')
# # 特征值与目标值
# X = data[data.columns[0:-1]]
# y = data[data.columns[-1]]
# 数据集的分割
x_train,x_test,y_train,y_test = train_test_split(X,y,train_size=0.7)
ridge_model = Ridge()
param_test = {'alpha':[0.01,0.03,0.05,0.07,0.1,0.5,0.8,1],
'normalize':[True,False]}
# scoring表示内部评价准则
gv_ridge = GridSearchCV(estimator=ridge_model,param_grid=param_test,scoring='neg_mean_squared_error',cv=5)
gv_ridge.fit(x_train,y_train)
print('最好的参数模型',gv_ridge.best_params_)
print('最优模型的评分值', gv_ridge.best_score_)
# 模型评价
final_model = Ridge(alpha=0.05,normalize=True)
final_model.fit(x_train,y_train)
# 预测值
y_predict = final_model.predict(x_test)
# MSE
print('mse =',mean_squared_error(y_test,y_predict))
# 模型保存
joblib.dump(final_model,'house_train_model.m')
# 模型读取
clf = joblib.load('house_train_model.m')
predict = clf.predict(x_test)
print('predict = ', predict)
运行结果:
最好的参数模型 {'alpha': 0.03, 'normalize': True}
最优模型的评分值 -24.989734166438268
mse = 26.374721342289842
predict = [27.62730422 21.27319992 26.38649443 0.72196531 38.65675597 29.23941796
36.05087796 32.56484169 19.96407992 16.14210164 16.36591237 39.28294151
19.48974731 25.66591558 23.86767948 23.36773203 30.53412109 12.93148209
31.90062094 16.50168194 28.14791315 20.65767579 38.18272154 15.09670314
21.64409899 22.81266938 25.53729586 32.43443113 23.82742374 24.70861029
22.93379668 17.28994811 30.34172645 32.80517236 16.22604066 17.55617785
33.78670965 32.57300009 6.57952313 32.00804666 21.4265085 19.34730491
20.07725354 22.31214738 28.56628025 31.5666024 13.30766307 24.17702657
20.64302316 18.64510293 25.37001 35.20837679 34.84288918 9.01544148
19.66147062 27.55259222 20.46740267 17.96642259 29.45846599 13.82903107
26.81102377 14.32780977 29.06308931 16.03184298 24.75331024 16.30822875
1.33163796 25.20157459 16.19686952 17.21700864 17.41561113 30.09389483
24.86098999 21.2736113 27.4927086 20.51293216 27.56503633 32.71561938
40.08115884 18.37243134 15.96894462 36.49683289 19.0338362 22.32138586
10.60387297 28.9322626 39.56328393 17.8112504 17.5708612 36.09136896
26.9348509 21.8172934 3.6852502 21.16247922 17.14071607 14.29479597
17.96274048 25.28054701 13.0337754 17.93145403 22.51553882 18.24708355
21.63908227 21.57939998 28.79933753 20.26456397 28.55153246 14.37094609
38.26441208 17.99169714 25.66888267 19.85234744 32.02285332 32.70743443
28.82426478 24.66041754 33.23250865 22.22008918 21.15294815 16.99037595
12.75121752 17.34729732 13.97161254 16.65531886 16.93867585 21.34770394
33.1052382 31.24409521 20.39510937 19.99361394 16.3314265 40.2090575
27.49263462 15.36703238 30.87557293 35.23519836 27.87455158 19.54911193
26.25636086 19.14095492 15.08194954 11.76916039 24.97622543 27.66718388
19.01087556 5.68797767 41.27947717 14.78844916 20.92050563 19.67098371
19.0361772 24.30077008]