最短路径算法-迪杰斯特拉(Dijkstra)算法
最短路径算法-迪杰斯特拉(Dijkstra)算法
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先遍历思想),直到扩展到终点为止。
基本思想
- 通过Dijkstra计算图G中的最短路径时,需要指定一个起点D(即从顶点D开始计算)。
- 此外,引进两个数组S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点D的距离)。
- 初始时,数组S中只有起点D;数组U中是除起点D之外的顶点,并且数组U中记录各顶点到起点D的距离。如果顶点与起点D不相邻,距离为无穷大。
- 然后,从数组U中找出路径最短的顶点K,并将其加入到数组S中;同时,从数组U中移除顶点K。接着,更新数组U中的各顶点到起点D的距离。
- 重复第4步操作,直到遍历完所有顶点。
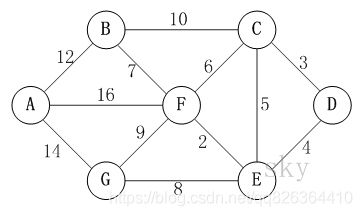
迪杰斯特拉(Dijkstra)算法图解
以上图为例,来对迪杰斯特拉进行算法演示(以顶点D为起点)。
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
迪杰斯特拉算法的C#实现
using System;
/**
* Dijkstra算法获取最短路径
*/
public class Dijkstra
{
public static int MAX = int.MaxValue;
// 邻接表中表对应的链表的顶点
public class ENode
{
public int ivex; // 该边所指向的顶点的位置
public int weight; // 该边的权
public ENode nextEdge; // 指向下一条弧的指针
}
// 邻接表中表的顶点
public class VNode
{
public char data; // 顶点信息
public ENode firstEdge; // 指向第一条依附该顶点的弧
}
// 边的结构体
public class EData
{
public char start; // 边的起点
public char end; // 边的终点
public int weight; // 边的权重
public EData(char start, char end, int weight)
{
this.start = start;
this.end = end;
this.weight = weight;
}
}
public int mEdgNum; // 边的数量
public VNode[] mVexs; // 顶点数组
/*
* 创建图
*
* 参数说明:
* vexs -- 顶点数组
* edges -- 边
*/
public Dijkstra(char[] vexs, EData[] edges)
{
// 初始化"顶点数"和"边数"
int vlen = vexs.Length;
int elen = edges.Length;
// 初始化"顶点"
mVexs = new VNode[vlen];
for (int i = 0; i < mVexs.Length; i++)
{
mVexs[i] = new VNode();
mVexs[i].data = vexs[i];
mVexs[i].firstEdge = null;
}
// 初始化"边"
mEdgNum = elen;
for (int i = 0; i < elen; i++)
{
// 读取边的起始顶点和结束顶点
char c1 = edges[i].start;
char c2 = edges[i].end;
int weight = edges[i].weight;
// 读取边的起始顶点和结束顶点
int p1 = GetPosition(c1);
int p2 = GetPosition(c2);
// 初始化node1
ENode node1 = new ENode();
node1.ivex = p2;
node1.weight = weight;
// 将node1链接到"p1所在链表的末尾"
if (mVexs[p1].firstEdge == null)
mVexs[p1].firstEdge = node1;
else
LinkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
ENode node2 = new ENode();
node2.ivex = p1;
node2.weight = weight;
// 将node2链接到"p2所在链表的末尾"
if (mVexs[p2].firstEdge == null)
mVexs[p2].firstEdge = node2;
else
LinkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 将node节点链接到list的最后
*/
private void LinkLast(ENode list, ENode node)
{
ENode p = list;
while (p.nextEdge != null)
p = p.nextEdge;
p.nextEdge = node;
}
/*
* 返回ch位置
*/
private int GetPosition(char ch)
{
for (int i = 0; i < mVexs.Length; i++)
if (mVexs[i].data == ch)
return i;
return -1;
}
/*
* 获取边的权值;若start和end不是连通的,则返回无穷大。
*/
private int GetWeight(int start, int end)
{
if (start == end)
return 0;
ENode node = mVexs[start].firstEdge;
while (node != null)
{
if (end == node.ivex)
return node.weight;
node = node.nextEdge;
}
return MAX;
}
/*
* Dijkstra最短路径。
* 即,统计图中"起点D"到其它各个顶点的最短路径。
*
* 参数说明:
* vs -- 起始顶点(start vertex)。
* prev -- 前驱顶点数组。即,prev[i]的值是"起点D"到"顶点i"的最短路径所经历的全部顶点中,位于"顶点i"之前的那个顶点。
* dist -- 长度数组。即,dist[i]是"起点D"到"顶点i"的最短路径的长度。
*/
public void CalcDijkstra(int vs, int[] prev, int[] dist)
{
// flag[i]=true表示"起点D"到"顶点i"的最短路径已成功获取。
bool[] flag = new bool[mVexs.Length];
// 初始化
for (int i = 0; i < mVexs.Length; i++)
{
flag[i] = false; // 顶点i的最短路径还没获取到。
prev[i] = 0; // 顶点i的前驱顶点为0。
dist[i] = GetWeight(vs, i); // 顶点i的最短路径为"起点D"到"顶点i"的权。
}
// 对"起点D"自身进行初始化
flag[vs] = true;
dist[vs] = 0;
// 遍历mVexs.Length-1次;每次找出一个顶点的最短路径。
int k = 0;
for (int i = 1; i < mVexs.Length; i++)
{
// 寻找当前最小的路径
// 即,在未获取最短路径的顶点中,找到离起点D最近的顶点(k)。
int min = MAX;
for (int j = 0; j < mVexs.Length; j++)
{
if (flag[j] == false && dist[j] < min)
{
min = dist[j];
k = j;
}
}
// 标记"顶点k"为已经获取到最短路径
flag[k] = true;
// 更新当前最短路径和前驱顶点
// 即,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
for (int j = 0; j < mVexs.Length; j++)
{
int tmp = GetWeight(k, j);
tmp = (tmp == MAX ? MAX : (min + tmp)); // 防止溢出
if (flag[j] == false && (tmp < dist[j]))
{
dist[j] = tmp;
prev[j] = k;
}
}
}
// 打印dijkstra最短路径的结果
Console.WriteLine("dijkstra({0}): \n", mVexs[vs].data);
for (int i = 0; i < mVexs.Length; i++)
{
Console.WriteLine("shortest({0}, {1})={2}\n", mVexs[vs].data, mVexs[i].data, dist[i]);
}
}
public static void Main(string[] args)
{
char[] vexs = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
EData[] edges = {
// 起点 终点 权重
new EData('A', 'B', 12),
new EData('A', 'F', 16),
new EData('A', 'G', 14),
new EData('B', 'C', 10),
new EData('B', 'F', 7),
new EData('C', 'D', 3),
new EData('C', 'E', 5),
new EData('C', 'F', 6),
new EData('D', 'E', 4),
new EData('E', 'F', 2),
new EData('E', 'G', 8),
new EData('F', 'G', 9),
};
Dijkstra pG = new Dijkstra(vexs, edges);
// dijkstra算法获取"起点D"到其它各个顶点的最短距离
int[] prev = new int[pG.mVexs.Length];
int[] dist = new int[pG.mVexs.Length];
pG.CalcDijkstra(3, prev, dist);
Console.ReadKey();
}
} 执行结果
参考:https://www.cnblogs.com/skywang12345/p/3711514.html