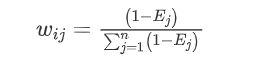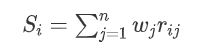熵权法 —— matlab
目录
一、熵权法介绍
二、熵权法赋权步骤
1.指标正向化
mapminmax介绍
2.数据标准化
3.计算信息熵
4.计算权重以及得分
三、实例分析
1.读取数据
2.指标正向化
2.1 越小越优型处理
2.2 某点最优型指标处理
3.数据标准化
4.计算信息熵
5.计算权重
6.计算得分
总结
一、熵权法介绍
熵权法是一种客观赋值方法。在具体使用的过程中,熵权法根据各指标的变异程度,利用信息熵计算出各指标的熵权,再通过熵权对各指标的权重进行修正,从而得到较为客观的指标权重。
一般来说,若某个指标的信息熵指标权重确定方法之熵权法越小,表明指标值得变异程度越大,提供的信息量越多,在综合评价中所能起到的作用也越大,其权重也就越大。
相反,若某个指标的信息熵指标权重确定方法之熵权法越大,表明指标值得变异程度越小,提供的信息量也越少,在综合评价中所起到的作用也越小,其权重也就越小。
二、熵权法赋权步骤
1.指标正向化
这个步骤视情况自己决定把。。。。
不同的指标代表含义不一样,有的指标越大越好,称为越大越优型指标。有的指标越小越好,称为越小越优型指标,而有些指标在某个点是最好的,称为某点最优型指标。为方便评价,应把所有指标转化成越大越优型指标。
设有m个待评对象,n个评价指标,可以构成数据矩阵
![]()
设数据矩阵内元素,经过指标正向化处理过后的元素为 (Xij)'
-
越小越优型指标:C,D属于此类指标
![]()
其他处理方法也可,只要指标性质不变即可
-
某点最优型指标:E属于此类指标
设最优点为a, 当a=90时E最优。
![]()
其他处理方法也可,只要指标性质不变即可
-
越大越优型指标:其余所有指标属于此类指标
![]()
此类指标可以不用处理,想要处理也可,只要指标性质不变
mapminmax介绍
最大最小值归一化
语法
[Y,PS] = mapminmax(X,YMIN,YMAX)
[Y,PS] = mapminmax(X,FP)
Y = mapminmax('apply',X,PS)
X = mapminmax('reverse',Y,PS)
说明:
[Y,PS] = mapminmax(X,YMIN,YMAX)mapminmax(X,YMIN,YMAX) 将矩阵的每一行压缩到 [YMIN,YMAX],其中当前行的最大值变为YMAX,最小值变为YMIN。PS为结构体储存相关信息,如最大最小值等
[Y,PS] = mapminmax(X,FP)其中FP为结构体类型,这时就是将矩阵的每一行压缩到[ FP.ymin, FP.ymax]中
Y = mapminmax('apply',X,PS)可以将之前储存的结构体应用到新的矩阵中,利用上一步得到的PS来映射X到Y
X = mapminmax('reverse',Y,PS)可按照之前数据规律,反归一化,利用归一化后的Y和PS重新得到X
2.数据标准化
因为每个指标的数量级不一样,需要把它们化到同一个范围内再比较。标准化的方法比较多,这里仅用最大最小值标准化方法。
设标准化后的数据矩阵元素为rij,由上可得指标正向化后数据矩阵元素为 (Xij)'
![]()
3.计算信息熵
![]()
为避免Pij零元素的出现出现计算错误,归一化最低区间可以从0.002开始。如果某个指标的信息熵Ej越小,就表明其指标值的变异程度越大,提供的 信息量也越大,可以认为该指标在综合评价起到作用也越大。
4.计算权重以及得分
权重为:
得分为:
三、实例分析
用一篇高引用的核心期刊论文[1]为例,针对各个银行的资产收益率,费用利润率,逾期贷款率,非生息资产率,流动性比率,资产使用率,自有资本率指标进行评价。设资产收益率为A,费用利润率为B,逾期贷款率为C,非生息资产率为D,流动性比率为E,资产使用率为F,自有资本率为G。数据表格如下:
1.读取数据
%读取数据
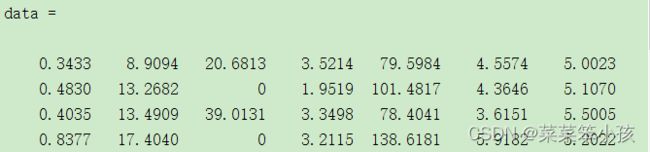
data=xlsread('D:\桌面\shangquan.xlsx')返回:
在这里,我们可以看到读取的数据中,有部分是我们不想要的,于是我们得做处理
data=data(:,3:end) %只取指标数据返回:
2.指标正向化
%指标正向 化处理后数据为data1
data1=data;2.1 越小越优型处理
%%越小越优型处理
index=[3,4];%越小越优指标位置
for i=1:length(index)
data1(:,index(i))=max(data(:,index(i)))-data(:,index(i))
end
返回:
2.2 某点最优型指标处理
%%某点最优型指标处理
index=[5];
a=90;%最优型数值
for i=1:length(index)
data1(:,index(i))=1-abs(data(:,index(i))-a)/max(abs(data(:,index(i))-a))
end返回:
3.数据标准化
data2=mapminmax(data1',0.002,1) %标准化到0.002-1区间返回:
由于是mapminmax对行进行标准化,所以需要转置一下
data2=data2'返回:
4.计算信息熵
%得到信息熵
[m,n]=size(data2);
p=zeros(m,n);
for j=1:n
p(:,j)=data2(:,j)/sum(data2(:,j))
end
for j=1:n
E(j)=-1/log(m)*sum(p(:,j).*log(p(:,j)))
end返回:
5.计算权重
%计算权重
w=(1-E)/sum(1-E)返回:
6.计算得分
%计算得分
s=data2*w';
Score=100*s/max(s);
disp('12个银行分别得分为:')
disp(Score)返回:
总结
clc;clear;
%读取数据
data=xlsread('D:\桌面\shangquan.xlsx');
data=data(:,3:end); %只取指标数据
%指标正向 化处理后数据为data1
data1=data;
%%越小越优型处理
index=[3,4];%越小越优指标位置
for i=1:length(index)
data1(:,index(i))=max(data(:,index(i)))-data(:,index(i));
end
%%某点最优型指标处理
index=[5];
a=90;%最优型数值
for i=1:length(index)
data1(:,index(i))=1-abs(data(:,index(i))-a)/max(abs(data(:,index(i))-a));
end
%数据标准化 mapminmax对行进行标准化,所以转置一下
data2=mapminmax(data1',0.002,1); %标准化到0.002-1区间
data2=data2';
%得到信息熵
[m,n]=size(data2);
p=zeros(m,n);
for j=1:n
p(:,j)=data2(:,j)/sum(data2(:,j));
end
for j=1:n
E(j)=-1/log(m)*sum(p(:,j).*log(p(:,j)));
end
%计算权重
w=(1-E)/sum(1-E);
%计算得分
s=data2*w';
Score=100*s/max(s);
disp('12个银行分别得分为:')
disp(Score)