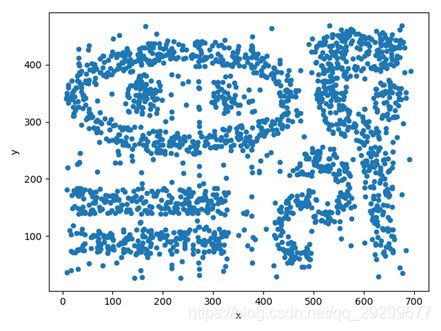
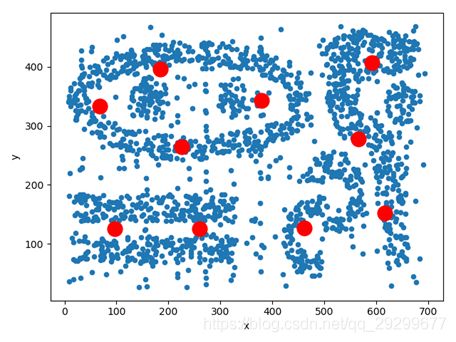
K均值与DBSCAN聚类效果

K均值与DBSCAN聚类效果

K均值的发展状况

K-means算法(Lloyod,1982)是简单而又有效的统计聚类算法，使机器能够将具有相同属性的样本归置到一块儿。K-均值算法的理论研究主要包括三块内容：（1）模型泛化；（2）搜索策略设计；（3）距离函数设计。
其中就有基于期望最大化（EM）算法的混合模型就是K均值算法的一种泛化形式，为了避免落入较差的局部最优点，在批量搜索的基础上继续进行增量搜索，可以提高聚类绩效，以及wu，xiong和Chen对适用K均值的距离函数发现，他们证明布莱格曼散度和余弦相似度都是K一均值距离的一个特例，并且针对化简后目标函数设计的新增量搜索策略SBIL，能够显著提高某些距离函数的聚类绩效，比如KL散度。
K一均值算法因其简单和高效性，还可以与聚类、关联以及分类等领域的其他方法结合起来，提高这些方法的数据分析性能。1.K均值算法与层次聚类法，因为凝聚层次法对数据中异常点非常敏感，而先用K均值法把数据分为K个簇再合成树可以提高绩效。2.K均值算法与关联分析，数据之间存在强相关模式即来自同一簇，因此先进行关联分析再用K均值聚类比较好。3K均值与模式分类，Wu等提出基于局部聚类的分类框架：COG，主要是再分类前对数据进行K均值聚类，以得到线性可分且比较均匀的子类 。
总结：如何搜索目标函数全局最优点或者较好的局部最优点仍然是难点，将算法与数据特点相结合是研究特点的要素之一。

k值怎样取更佳？

1.手肘法

理论：手肘法的核心指标是SSE(sum of the squared errors，误差平方和)

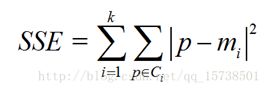
其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。
手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

2.轮廓系数法

理论: 该方法的核心指标是轮廓系数（Silhouette Coefficient），某个样本点Xi的轮廓系数定义如下：

其中，a是Xi与同簇的其他样本的平均距离，称为凝聚度，b是Xi与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是

其中p是某个簇Ck中的样本。事实上，简单点讲，就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。

   求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

如何确定K值实验演示:

数据集来自: http://www.cse.msu.edu/~ptan/dmbook/software/
发现数据集的格式不能对应，使用的是自制数据，数据文件名：hand_data.xlsx
程序运行效果图：


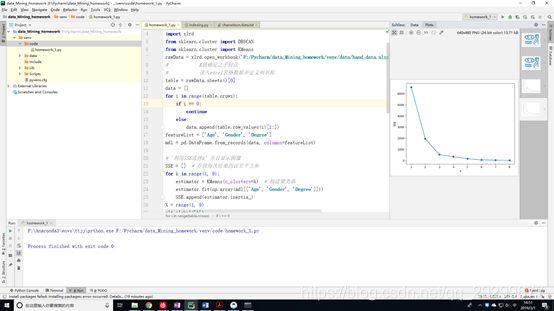
由图可知，当SSE随K值增加的时候SSE出现大幅度的降低然后出现小幅度的降低并且趋于平缓，而肘部数据即K=3时是最优K值。手肘法比较符合K均值的核心思想。


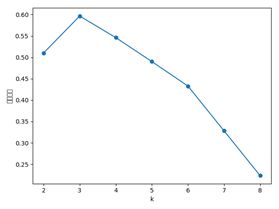
由图可知选择最高点即K=3时，轮廓系数最大为最好的情况。

初始质心怎样取更佳？

1.k-means++算法实现

1.	import pandas as pd  
2.	import numpy as np  
3.	import matplotlib.pyplot as plt  
4.	from sklearn.cluster import KMeans  
5.	data = pd.read_csv('F:/Pycharm/data_Mining_homework/venv/data/chameleon.data.txt', delimiter=' ', names=['x','y'])  
6.	data.plot.scatter(x='x',y='y')  
7.	estimator = KMeans(n_clusters=10)#构造聚类器  
8.	estimator.fit(data)#聚类  
9.	label_pred = estimator.labels_ #获取聚类标签  
10.	centroids = estimator.cluster_centers_ #获取聚类中心  
11.	inertia = estimator.inertia_ # 获取聚类准则的总和  
12.	x1 = centroids[:,0]  
13.	y1 = centroids[:,1]  
14.	plt.scatter(x1,y1,c = 'r',marker='o',linewidths='10')  
15.	plt.show() 

该段代码实现的是k-means++算法对质心进行选择的，具体的源码如下:

1.	# Pick first center randomly  
2.	    center_id = random_state.randint(n_samples)  
3.	    if sp.issparse(X):  
4.	        centers[0] = X[center_id].toarray()  
5.	    else:  
6.	        centers[0] = X[center_id]  
7.	    # Initialize list of closest distances and calculate current potential  
8.	    closest_dist_sq = euclidean_distances(  
9.	        centers[0, np.newaxis], X, Y_norm_squared=x_squared_norms,  
10.	        squared=True)  
11.	    current_pot = closest_dist_sq.sum()  
12.	    # Pick the remaining n_clusters-1 points  
13.	    for c in range(1, n_clusters):  
14.	        # Choose center candidates by sampling with probability proportional
15.	        # to the squared distance to the closest existing center  
16.	        rand_vals = random_state.random_sample(n_local_trials) * current_po 
17.	        candidate_ids = np.searchsorted(stable_cumsum(closest_dist_sq),  
18.	                                        rand_vals)  
19.	        # Compute distances to center candidates  
20.	        distance_to_candidates = euclidean_distances(  
21.	            X[candidate_ids], X, Y_norm_squared=x_squared_norms, squared=True)  
22.	        # Decide which candidate is the best  
23.	        best_candidate = None  
24.	        best_pot = None  
25.	        best_dist_sq = None  
26.	        for trial in range(n_local_trials):  
27.	            # Compute potential when including center candidate  
28.	            new_dist_sq = np.minimum(closest_dist_sq,  
29.	                                     distance_to_candidates[trial])  
30.	            new_pot = new_dist_sq.sum()  
31.	            # Store result if it is the best local trial so far  
32.	            if (best_candidate is None) or (new_pot < best_pot):  
33.	                best_candidate = candidate_ids[trial]  
34.	                best_pot = new_pot  
35.	                best_dist_sq = new_dist_sq  

该算法的核心思想是这样进行的，首先是随机的选择第一个中心点，然后根据这个中心点和其余点的坐标来计算距离来计算可能的概率，接下来选取其余的n-1个质心的坐标，根据这些候选点距离中心点的距离的平方成反比的可能性进行选择，然后把最好的中心点保存下来。这样就实现了对初试质心的选择，即选择距离较远的那些点。
同时我们可以根据算法知道，每次计算的中心点都不一样，会有所差别，因为第一个点是随机选择的，然后如果第一个随机点是离群点或者异常点将对聚类分析影响很大，下图右边可以明显看出选择的聚类中心点发生了变化，黑点右边上边有两个，而红点右边只有一个。
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200626104308383.png
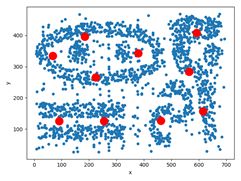
我们可以发现k-means++这种算法对于上述数据不能很好的处理聚类结果，我们选择密度聚类的方法来优化这个聚类效果。

2.密度聚类

主要使用的是基于密度聚类的DBSCAN算法，该算法的核心思想是给定一个半径即Eps，在这个范围内的点数都成一簇，同时任何与核心点足够靠近的边界点也放到与核心点相同的簇中。
代码如下：

1.	import pandas as pd  
2.	import numpy as np  
3.	import matplotlib.pyplot as plt  
4.	from sklearn.cluster import KMeans  
5.	from sklearn.cluster import DBSCAN  
6.	data = pd.read_csv('F:/Pycharm/data_Mining_homework/venv/data/chameleon.data.txt', delimiter=' ', names=['x','y'])  
7.	data.plot.scatter(x='x',y='y')  
8.	db = DBSCAN(eps=15.5, min_samples=5).fit(data)  
9.	core_samples_mask = np.zeros_like(db.labels_, dtype=bool)  
10.	core_samples_mask[db.core_sample_indices_] = True  
11.	labels = pd.DataFrame(db.labels_,columns=['Cluster ID'])  
12.	result = pd.concat((data,labels), axis=1)  
13.	result.plot.scatter(x='x',y='y',c='Cluster ID', colormap='jet')  
14.	plt.show()  

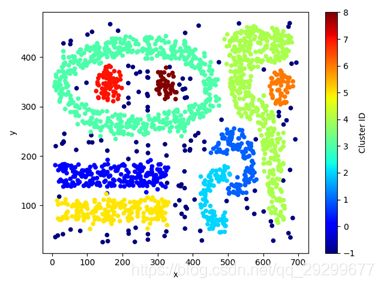
我们可以对比k-means算法聚类的效果图，可以明显的发现聚类的效果特别好，一共有10个分类，从-1到8每个类的颜色对应不同，而k-means的分类结果不确定，而且没有很好的分出具体的类，对数据的凸显性太差，而且对噪声点和异常点特别的敏感，如果随机选择的过程中把这些点选择造成结果的分类很不准确，而DBSCAN算法先按照收敛半径Eps，分类出核心点，边界点或噪声点，然后运行中去除噪声点的干扰，避免了k-means++算法的缺点之一，而DBSCAN算法的关键在于收敛半径的选择上，如果Eps太小，则每个点周围都只有它自己，如果太大则全部都在一起，上述代码是直接根据数据的特征选择的esp =15.5，无法进行分类，一个好的思路就是采用grid，把数据集划分为一个个小格子，每个小格子代表周围 。

[1] .K—means CIustering：The Research Frontier and Future Directions
WU Junjiel， CHEN Jianl，XIONG Hui
[2] https://blog.csdn.net/qq_15738501/article/details/79036255
[3] https://blog.csdn.net/github_39261590/article/details/76910689
[4] http://www.cse.msu.edu/~ptan/dmbook/software/
[5] http://www.cse.msu.edu/~ptan/dmbook/tutorials/tutorial8/tutorial8.html#8.3.3-Group- Average
[6] https://blog.csdn.net/sinat_27612639/article/details/70257972