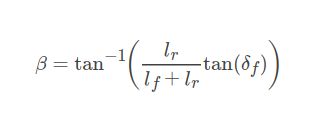无人驾驶-控制-自行车模型

无人驾驶-控制-自行车模型

一、综述

1.1 简介

在了解高级的车辆控制算法之前，掌握车辆运动模型是非常有必要的。车辆运动模型就
是一类能够描述我们的车辆的运动规律的模型。显然，越复杂的模型就越接近现实中的
车辆运动规律，本节我们一起了解一下两个广泛使用的车辆模型——运动学自行车模型
和动力学自行车模型。

无人驾驶系统往往分成感知，决策和控制三个模块，其中无人车的路径规划和底层控制是工作在不同的层的，路径规划层往往会基于更加高层的（感知层，定位层）的信息和底层的（控制层）的实时信息指定行驶的路径，那么从路径规划层传来的就是车辆的参考路径，控制系统需要做的就是严格按照这个参考路径（以及速度等控制输入量）去驾驶我们的车辆，一般来说，我们会用多项式的行驶来描述这个路径曲线，三次多项式就可以描述绝大多数的路径了。

参考链接: 三阶多项式-最小二乘法推导.

1.2 模型预测控制

无人车的控制依赖于一项称为模型预测控制(Model Predictive Control) 的简单技术，这种控制的方法是产生一系列的可行的（也就是说在实际上车辆能够做到的）控制输入，基于一定的算法（往往是带约束的非线性优化算法）来调整这一系列的控制输入，使得一个损失函数(cost function) 最小化，这个损失函数的求解就要依赖于车辆的运动学或者动力学模型的输出和参考的路径的差值求得，这些模型正是本节介绍的内容。

1.3 自行车模型

首先我们要简化汽车运动，其中自行车模型就是简单且有效的简化方式。自行车模型基于如下几个假设：

• 车辆在垂直方向的运动被忽略掉了，也就是说我们描述的车辆是一个二维平面上的运动物体（可以等价与我们是站在天空中的俯视视角）
• 我们假设车辆的结构就像自行车一样，也就是说车辆的前面两个轮胎拥有一直的角度和转速等，同样后面的两个轮胎也是如此，那么前后的轮胎就可以各用一个轮胎来描述
• 我们假设车辆运动也和自行车一样，这意味着是前面的轮胎控制这车辆的转角

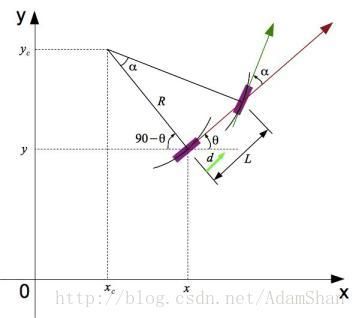
首先我们简单的在一个二维平面上描述一个车辆：

其中 θ是其在 Yaw 方向的偏转角度，它是相对于 x 轴的逆时针方向的角度，v 是 θ 方向的速度，L 是车辆的轴距（前后轮胎的距离）, (x,y) 是车辆的坐标。

下图是该车辆的自行车模型：

二、运动学模型

2.1 模型定义

作为一种自行车模型，运动学自行车模型也假定车辆形如一辆自行车，整个的控制量可以简化为 (a, δf) ，其中 a 是车辆的加速度，踩油门踏板意味着正的加速度，踩刹车踏板意味着负的加速度。δf 是我们的方向盘转角，我们假定这个方向盘转角就是前轮胎当前的转角。这样，我们使用两个量描述了车辆的控制输入(control input)。

然后我们定义我们模型中的状态量，运动学自行车模型使用四个状态量来描述车辆的当前状态：

• x : 即车辆当前的 x 坐标
• y : 即车辆当前的 y 坐标
• ψ : 即车辆当前的偏航角（Yaw 方向的偏角，通常用弧度描述, 逆时针方向为正）
• v : 即车辆的速度

一个简单的运动学自行车模型如图所示：

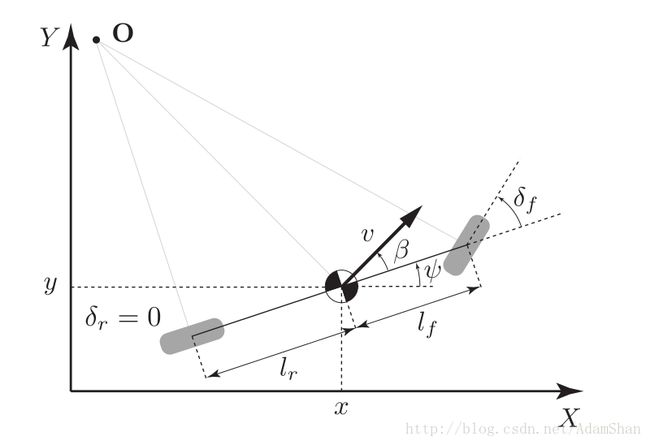
其中 lf 和 lr 为前轮和后轮到车辆重心的距离。那么更具运动学定理，运动学自行车模型中的各个状态量的更新公式如下：

其中偏航角的更新公式:

Vt * sin(β) / Lr = Wt, Wt * dt = β

2.2 偏航角推导

其中 β 可以由如下公式推导求得：

tan β = lr / dist;
tan δf = (lr + lf) / dist;
其中，利用互余性，β 和 δf 可以转换成以O为顶点的角，再根据三角形正切关系，可以得到 tan β / tan δf = (lr / dist) / [(lr + lf) / dist] = lf / (lf + lr)

由于绝大多数的汽车后轮都不能够偏转，所以我们的自行车模型就假定后轮的转角控制输入 δr=0，即方向盘上的控制输入，都反映到了前轮的转角上。

那么基于这个简单的运动学自行车模型，在给定了一个时刻的控制输入以后，我们可以计算求得 dt 时间以后我们车辆的状态信息（坐标，偏航角以及速度），那么这个模型就可以作为我们模型预测控制下的基础车辆模型了。

三、动力学模型

3.1 模型简介

前面的车辆运动学自行车模型其实还隐含着一个重要的假设，那就是，车前轮的方向即是车辆当前的速度方向，在实际车辆运动过程中，当车辆在以相对高的速度行驶时，车轮的方向并不一定车辆当前的速度方向，这个时候，我们引入车辆的动力学自行车模型。

车辆动力学模型通过对轮胎和路面之间的复杂相互作用来描述车辆的运动。在一个动力模型中，我们需要考虑各种各样的力的作用，可大致分为两类： 纵向力和侧向力，纵向力是使车辆前后移动的力量，而侧向力是使车辆在横向移动，在力的相互作用过程中，轮胎起着决定性的作用。对于车来说，研究车辆动力学，主要是研究车辆轮胎及其相关部件的受力情况。比如纵向速度控制，通过控制轮胎转速实现；横向航向控制，通过控制轮胎转角实现。

3.2 受力分析

正常情况下，车辆上的作用力沿着三个不同的轴分布：

• 纵轴上的力包括驱动力和制动力，以及滚动阻力和拖拽阻力作滚摆运动；
• 横轴上的力包括转向力、离心力和侧风力，汽车绕横轴作俯仰运动；
• 立轴上的力包括车辆上下振荡施加的力，汽车绕立轴作偏摆或转向运动

车辆受力模型：

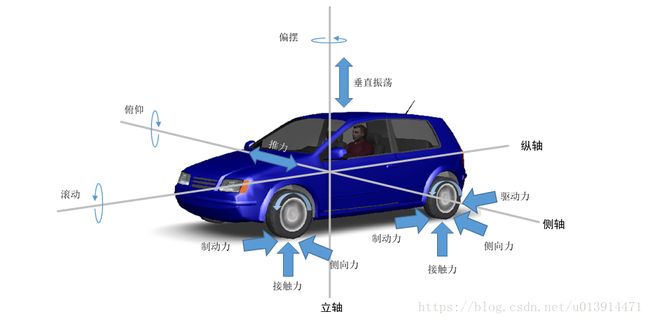
而在单车模型假设的前提下，再作如下假设，即可简单搭建车辆的动力学模型：

• 只考虑纯侧偏轮胎特性，忽略轮胎力的纵横向耦合关系；
• 用单车模型来描述车辆的运动，不考虑载荷的左右转移；
• 忽略横纵向空气动力学；

车辆动力学模型：

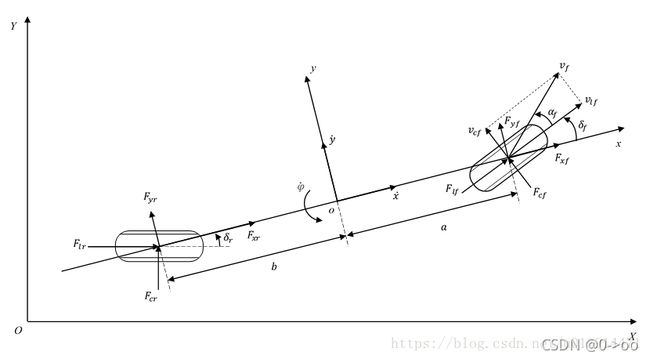
如上图所示，oxyz为固定于车身的车辆坐标系，OXY为固定于地面的惯性坐标系。
单车模型的车辆具有2个自由度：绕z轴的横摆运动，和沿x轴的纵向运动。纵向指沿物体前进方向，横向(或侧向)指垂直纵向方向。

• 横向运动：出自横向的风力，以及曲线行驶时的离心力等。
• 纵向运动：受总驱动阻力、加速、减速等的影响。总驱动阻力由滚动阻力、拖拽阻力和坡度阻力等构成。
• 滑移角：轮胎方向和轮胎速度方向的夹角。滑移角的产生主要是由于车轮所受合力方向并非朝向车轮行进方向，但车轮的偏移角通常较小。

上图中各符号定义：

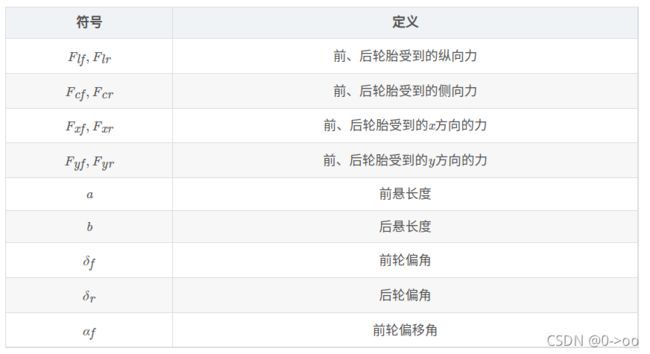
根据牛顿第二定律，分别沿x轴、y轴和z轴作受力分析：

在x轴方向上：

m * a_x = Fxf + Fxr

在y轴方向上：

m * a_y = Fyf + Fyr

在z轴方向上：

Iz * ¨φ = a * Fyf - b * Fyr

其中，m 为整车质量，Iz 为车辆绕z轴转动的转动惯量，x轴方向的运动（绕纵轴的滚动运动）可暂不用考虑。

3.3 横向动力学

（1）y轴方向上公式


（2）轮胎公式

由于轮胎受到的横向压力，轮胎会有一个很小的滑移角，如图所示

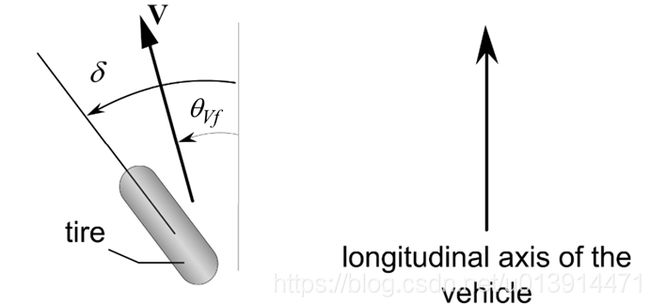
（2.1）前轮/后轮滑移角

滑移角与侧偏刚度的关系式:

（2.2）前轮/后轮速度方向

（2.3）动力学模型

（3）方向盘控制模型

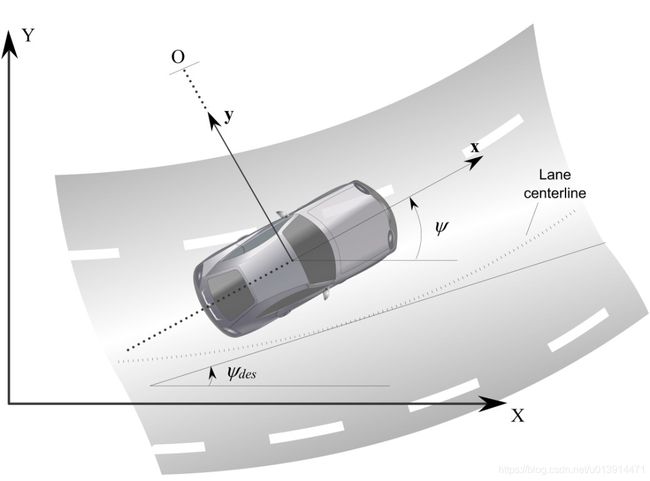
上面提到，横向控制主要通过控制轮胎转角实现，而对于驾驶员来说，可直接操控的是方向盘角度，因此在搭建车辆动力学模型时，可以以相对于道路的方向和距离误差为状态变量的动力学模型。

假设，e1为横向误差，车辆质心距车道中心线的距离，e2 为航向误差，车辆纵向速度为Vx，车辆转弯半径为R，则：


（4）方向盘控制的动力学模型

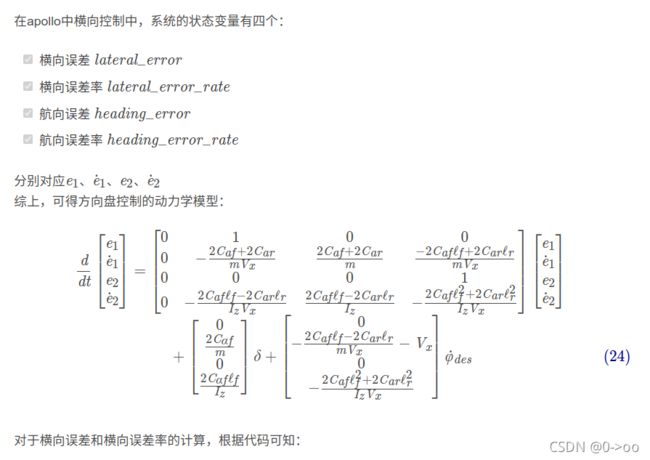
3.4 横向误差分析

（1）横向误差示意图

（2）横向误差表达式

参考链接

1. https://blog.csdn.net/u013914471
2. https://blog.csdn.net/adamshan/article/details/78696874