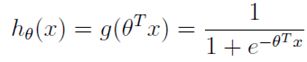【学习笔记-时间序列预测】Prophet-模型原理
一、模型概述
1.1 适用场景
A modular regression model with interpretable parameters 模块化回归、有可解释参数模型
Facebook开源的时间序列预测算法，适用于具有规律的数据，适用情景如下：
- a.有至少几个月（最好是一年）的每小时、每天或每周观察的历史数据；
- b.有多种人类规模级别的较强的季节性趋势：每周的一些天和每年的一些时间；
- c.有事先知道的以不定期的间隔发生的重要节假日（比如国庆节）；
- d.缺失的历史数据或较大的异常数据的数量在合理范围内；
- e.有历史趋势的变化（比如因为产品发布）；
- f.对于数据中蕴含的非线性增长的趋势都有一个自然极限或饱和状态。
1.2 模型输入输出
3、Prophet 算法的输入输出
输出图包括：
-
原始的时间序列离散点
-
使用时间序列来拟合所得到的取值
-
时间序列的一个置信区间，（合理的上界和下界）
-
prophet 所做的事情就是：
-
输入已知的时间序列的时间戳和相应的值；
-
输入需要预测的时间序列的长度；
-
输出未来的时间序列走势。
-
输出结果可以提供必要的统计指标，包括拟合曲线，上界和下界等。
-
传入prophet的数据分为两列 ds 和 y ,ds表示时间序列的时间戳，y表示时间序列的取值
其中：
-
ds是pandas的日期格式，样式类似与
YYYY-MM-DD for a date or YYYY-MM-DD HH:MM:SS； -
y列必须是数值型，代表着我们希望预测的值。
通过 prophet 的计算，可以计算出：
-
yhat，表示时间序列的预测值
-
yhat_lower，表示预测值的下界
-
yhat_upper，表示预测值的上界
二、基本原理
这是Generalized Additive Model(GAM)模型的特例，通过对各项的拟合，再进行累加得到预测值。
模型整体由三部分组成：
- g(t): 趋势项，描述growth(增长趋势)，即时间序列非周期的变化趋势
- s(t): 周期项，描述seasonality(季节趋势)，即时间序列周期的变化
- h(t): 假期项，描述holidays(节假日对预测值的影响)，即周期中偶发的、无固定周期的假日对预测值的影响。
- ϵt：噪声项/误差项，随机的未预测波动。假设服从高斯分布(Gaussian distribution)/正态分布(Normal distribution)。
Prophet 算法就是通过拟合这几项，然后最后把它们累加起来就得到了时间序列的预测值。
2.1 趋势项(The trend model)
2.1.1 概述
趋势项用于描述时间序列非周期的变化趋势，包括基于逻辑回归函数的饱和增长模型(saturating growth model)、线性增长模型(piecewise linear model)。
2.1.2 基于逻辑回归的趋势项:
其中，C表示承载能力(capacity)，k表示增长率(growth rate)，m表示偏移量(offset parameter)
-
承载能力C(capacity):
- 用函数C(t)描述的随时间变化的函数，对增长的上限进行约束
- 在使用 Prophet 的 growth = ‘logistic’ 的时候，需要提前设置好 C(t) 的取值才行
-
增长率k(growth rate):
-
增长率不是恒定不变的，模型需要包含变化的增长率，从而拟合历史数据。需要定义增长率k变化的变化点(changepoints)，用来记录趋势的变化。
-
在 Prophet 里面，是需要设置变化点的位置的，而每一段的趋势和走势也是会根据变点的情况而改变的。确定变化点方法见下，确定变化点后，得到变化点的集合，假设集合中有s个元素（变化点），对应的时间为
(j=1,2...,s)，在该变化点趋势的变化通过增长率变化来描述。使用向量装载：
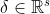, 其中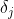 
表示在时间 上的增长率的变化量。增长率使用 k 来代替，得到在时间 t 上的增长率 -
-
通过指示函数
-
在时间 t 上面的增长率可以记作
-
-
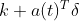
偏移量(offset parameter)
- 当增长率k调整后，每个变化点对应的偏移量j有以下计算公式
-
综上所述，得到趋势项的函数表达式
其中，k 表示增长率表示增长率的变化量,m 表示偏移量
2.1.3 变化点的线性趋势
若预测情景中出现不饱和增长，可以使用分段恒定增长率进行描述
2.1.4 变点的选择
先指定大量的变化点，并且假设增长率变化量满足
先验~
调整不会影响k，因此当参数
趋近于0时，拟合为非分段线性函数或逻辑回归函数。
Laplace先验
先验是对一种未知的东西的假设
比如说我们看到一个正方体的骰子，那么我们会假设他的各个面朝上的概率都是1/6，这个就是先验。但事实上骰子的材质可能是密度不均的，所以还要从数据集中学习到更接近现实情况的概率。
同样，在机器学习中，我们会根据一些已知的知识对参数的分布进行一定的假设，这个就是先验。有先验的好处是可以在较小的数据集中有良好的泛化性能，当然这是在先验分布是接近真实分布的情况下得到的了，从信息论的角度看，向系统加入了正确先验这个信息，肯定会提高系统的性能。
我们假设参数
满足如下的Laplace分布，这就是Laplace先验：
其中
是控制参数
逻辑回归函数
Logistic函数
逻辑回归使用一个函数来归一化y值，使y的取值在区间(0,1)内，这个函数称为Logistic函数(logistic function)，也称为Sigmoid函数(sigmoid function)。函数公式如下：
当z趋近于无穷大时，g(z)趋近于1；当z趋近于无穷小时，g(z)趋近于0。
逻辑回归函数表达式
逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0到1之间。线性回归模型的表达式带入g(z)，就得到逻辑回归的表达式:
依照惯例，让
表达式就转换为：
模型中有三个重要指标：
- changepoint_range 变化点的选取范围：是个百分比，默认为0.8，即在时间序列前80%的区间内选取变化点。
- n_changepoint 变化点的个数：默认在上述范围内选取25个变化点。
- changepoint_prior_scale 增长的变化率：变化点对应增长率的分布情况。
对于变化点的选择有两种方法，一种是人工指定；一种通过算法自动选择。
在默认的函数中，算法在时间序列的前 80% 的区间内设置变点，通过等分选择 n_changepoints = 25 个变点。由于变化点的增长率满足Laplace分布，当之后还要看一些边界条件是否合理，例如时间序列的点数是否少于 n_changepoints 等内容；其次如果边界条件符合，那变点的位置就是均匀分布的。
2.1.5 对未来的预测
- 从历史上长度为T的数据中，可以选择出 S 个变点，它们所对应的增长率的变化量满足~
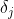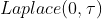
- 为了对未来进行预测，设置相应的变点的位置，使用 Poisson 分布等概率分布方法找到新增的变化点 changepoint_ts_new 的位置
- 与之前的变化点 changepoint_t 拼接，得到整段序列的变化点 changepoint_ts。
2.2 季节性趋势 s(t)
使用傅立叶级数来模拟时间序列的周期性：假设 P 表示时间序列的周期，P = 365.25 表示以年为周期，P = 7 表示以周为周期。
傅立叶级数形式是
其中，N表示希望在模型中使用的周期个数，N值较大时，可以拟合出更复杂的季节性函数，但也会带来过拟合问题。
对季节性的拟合需要2N个参数，记为向量![\beta=[a_1,b_1,...,a_N,b_N]^T](http://img.e-com-net.com/image/info8/343539ee2053465783b4f90f7e47419f.gif){kind=small}
这需要对每个历史值、预测值中的时间t去构造关于季节性趋势的向量，最终组合成矩阵。举个例子，以年为季节性周期，取N=10，得到
![X(t)=[cos(\frac{2\pi (1)t}{365.25}),...,sin(\frac{2\pi(10)t}{365.25})]](http://img.e-com-net.com/image/info8/0cdc4965fff64612a86a55c900670713.gif){kind=small}
一般来说，参数N的选择为N=10,N=3，参数的选择可以通过模型选择程序自动进行。
进一步地，通过矩阵的分量得到描述时间序列的季节项
假定参数β具有正态分布先验
~
通过 seasonality_prior_scale 控制，即 \sigma= seasonality_prior_scale。值越大，季节的效应越明显；值越小，表示季节的效应越不明显。
seasonality_mode 对应两种模式，分别是加法和乘法，默认是加法的形式。
2.3节假日趋势h(t)
根据生活经验，节假日、重要事项的影响持续时间不同，同时，假期前后几天的时间都比较重要，假设假期附近时间影响与假期当天一致。于是，需要将不同节假日的影响独立分析，不同的节假日需要设定不同的影响时间范围。
记
为第i个节假日的前后一段时间，使用参数
描述节假日影响范围，满足正态分布，
~
，默认值是10，可以调整。其中，v= holidays_prior_scale为可调整的参数。
假设共有L个节假日，得到节假日趋势公式
