2020.11.28-LeetCode第40场双周赛复盘(2easy1medium1hard)

2020.11.28-LeetCode第40场双周赛复盘

不定期参加周赛、双周赛，希望不管难度，搞懂每一次参加竞赛的所有题目

目录

5557. 最大重复子字符串（easy）

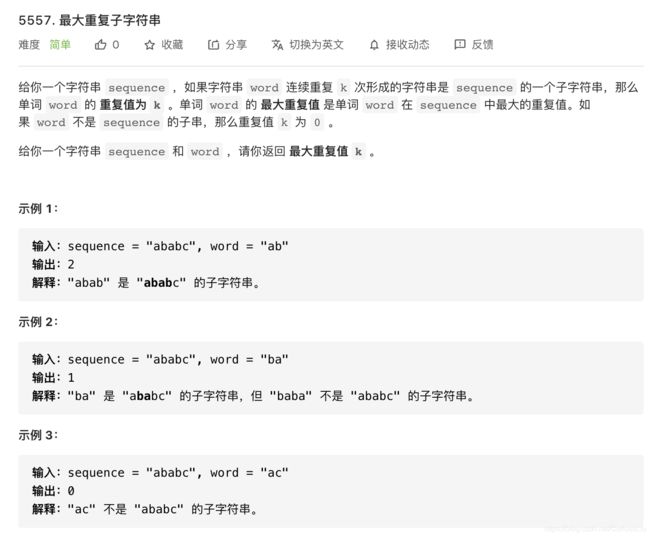
题目

题目分析

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

5558. 合并两个链表（medium）

题目

题目分析

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

5560. 设计前中后队列（medium）

题目

题目分析

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

5559. 得到山形数组的最少删除次数（hard）

题目

题目分析

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

---

5557. 最大重复子字符串（easy）

题目

题目分析

该题一开始希望找到一些函数调用的方法，但是似乎没有找到比较期望的函数，再加上应该是一道签到题，就沿用了之前C/C++语言解题的思想，一段一段找，如果找到了让i跳出这个单词长度的距离，如果没有找到则让i+= 1。

这个题个人记录需要注意的问题是在python提供的for循环中，即使使用了for i in range(xxx): 在循环体内部仍然无法对i变量进行修改，示意如下：

>>> for i in range(0,5):
...     i += 1
...     print("i:", i)
... 
i: 1
i: 2
i: 3
i: 4
i: 5

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

class Solution(object):
    def maxRepeating(self, sequence, word):
        """
        :type sequence: str
        :type word: str
        :rtype: int
        """
        maxCount = 0
        count = 0
        lenWord = len(word)
        i = 0
        while i maxCount:
                    maxCount = count
            else:
                i += 1
                count = 0

        return maxCount

5558. 合并两个链表（medium）

题目

题目分析

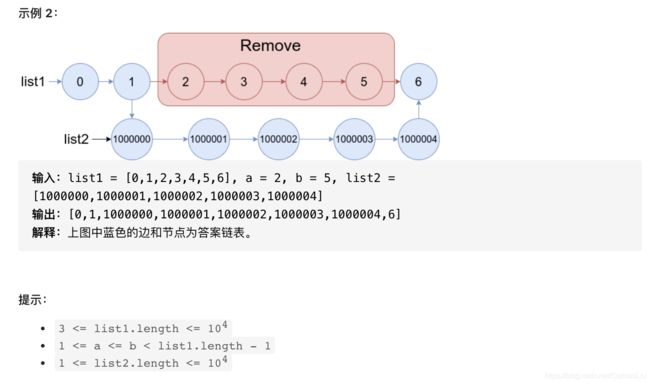
链表操作题，关键在于开始要记录对于list1中最终结尾拼接的位置处，可以先用list1往后走b次找到这个位置，之后进行整体链表的拼接即可

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def mergeInBetween(self, list1, a, b, list2):
        """
        :type list1: ListNode
        :type a: int
        :type b: int
        :type list2: ListNode
        :rtype: ListNode
        """
        countList1 = 0
        countList2 = 0
        head = list1
        headB = list1
        
        while headB and countList2 <= b:
            countList2 += 1
            headB = headB.next
        
        while head and countList1 < a-1:
            countList1 += 1
            head = head.next
            
        head.next = list2
        
        while list2.next:
            list2 = list2.next
        list2.next = headB
        
        return list1
        

5560. 设计前中后队列（medium）

题目

题目分析

该题其实是一道发挥空间较大的题，同时也是面试比较常见类型的，实现一个具体内容的题目，目前仅使用了在做题过程中想到的数组模拟办法，其他办法以及该数组模拟方法的时空复杂度均有待进一步分析

代码实现上其实就是对于角标的计算，拼接等操作，注意如果使用list.insert(targetIndex, value)在中间插入，和删除中间的元素，角标的计算方式是不同的

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

class FrontMiddleBackQueue(object):

    def __init__(self):
        self.queue = list()


    def pushFront(self, val):
        """
        :type val: int
        :rtype: None
        """
        self.queue.insert(0, val) # 0处插入val
        print(self.queue)


    def pushMiddle(self, val):
        """
        :type val: int
        :rtype: None
        """
        middle =  (len(self.queue)) // 2
        self.queue.insert(middle, val)
        print(self.queue)
        


    def pushBack(self, val):
        """
        :type val: int
        :rtype: None
        """
        self.queue.append(val)
        print(self.queue)


    def popFront(self):
        """
        :rtype: int
        """
        try:
            print("hello", self.queue)
            tempFront = self.queue[0]
            self.queue = self.queue[1:]
            return tempFront
        except:
            return -1
        
        


    def popMiddle(self):
        """
        :rtype: int
        """
        try:
            middle =  (len(self.queue)-1) // 2
            tempMiddle = self.queue[middle]

            self.queue = self.queue[0:middle] + self.queue[middle+1:]
            return tempMiddle
        except:
            return -1
        


    def popBack(self):
        """
        :rtype: int
        """
        try:
            tempBack = self.queue[-1]
            self.queue = self.queue[0:len(self.queue)-1]
            return tempBack
        except:
            return -1



# Your FrontMiddleBackQueue object will be instantiated and called as such:
# obj = FrontMiddleBackQueue()
# obj.pushFront(val)
# obj.pushMiddle(val)
# obj.pushBack(val)
# param_4 = obj.popFront()
# param_5 = obj.popMiddle()
# param_6 = obj.popBack()

5559. 得到山形数组的最少删除次数（hard）

题目

题目分析

在答案提示下该题是经典的最长上升子序列算法（LIS：Longest Increasing Subsequence）的变种，一个山峰可以看做一遍从正向的最长上升子列，和一遍从逆向的最长上升子列，为了取到一个使得两者都更优的点，在选取“山峰尖”的时候，需要综合考虑该点在正向和逆向的表现，这里还有一个难绕过来的点：正向求最长上升子列，得到的列表是一个正的最长上升；逆向求最长上升子列，得到的列表是一个逆向的最长上升。以目标结果来看，期望综合两个序列选择一个最优“山峰尖”点，假设期望选择第0个元素作为山峰尖点（注*：实际上根据要求开头，结尾点不能做山峰尖点），这时候应该统计正向上升到第0个位置处的最长上升子列，以及负向上升到第len(nums)-1位置处的点的最长上升序列，对两者进行加和后，减1去掉该点的重复计算。

对于LIS问题的补充说明：最长上升子列的问题是一个经典的DP问题，对于此类问题首先再在本博客中归纳特征：将一组序列改变为另一组序列，的最小次数，设置dpArray数组作为一维DP数组，其中每个dp位置处的代表意义是：对于序列的当前角标位置处，所能达到的最长上升长度。

为此，对该位置的值进行求解，需要从0开始遍历该位置之前的dp序列，代表对于之前每个位置处，所能达到的最长上升序列长度，于是如果该位置处的元素大于了之前的某个元素，也就是说构成了上升序列，那就可以使得当前位置处的dp状态等于这一被大于位置处的dp状态+1，另需要注意由于当前位置可能大于多个当前位置的之前位置，需要比较这些值，以获取最大的上升子序列。

代码解答（注：未重构代码，代码质量可能较差，也希望在学习做题过程中不断提升）

def findMaxUpperList(tempList):
    dpArray = [1 for x in range(len(tempList))] # memset全为1，LIS最小是1
    for i in range(1, len(tempList)):
        maxx = 1
        for j in range(0, i): # 从前到现在
            if tempList[i] > tempList[j]: # 如果上升，找到一个能使得其最长上升的  也就是说dpArray是相较于这个位置，找到能使得自己最长上升的
                if dpArray[j] + 1 > maxx:
                    maxx = dpArray[j] + 1
                    dpArray[i] = maxx
    return dpArray


class Solution(object):
    def minimumMountainRemovals(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        a = findMaxUpperList(nums)
        b = findMaxUpperList(nums[::-1])

        tempMax = 0
        for i in range(1, len(a)-1): # 为什么不从0开始(为什么掐头去尾) -> 山顶不能出现在左右两边
            if a[i] + b[len(a)-i-1] - 1 > tempMax:
                tempMax = a[i] + b[len(a)-i-1] - 1 # 一正一反，两个上升


        return len(a) - tempMax