【机器学习】基于多元时间序列对高考预测分析案例

本文借助 ARIMA模型，通过对中国的往年高考录取率进行建模和预测，并验证和检验模型精度和可行性，来应用模型来估计未来的录取率，进一步得出2030年中国高考录取率的预测值。

作者简介：理智，河北科技大学的大三学生，主攻深度学习。和大多数程序员一样，他是个乐观主义者，大量的时间都在调试代码，在调试中满怀希望，克服遇到的无数挫折。

01 数据来源

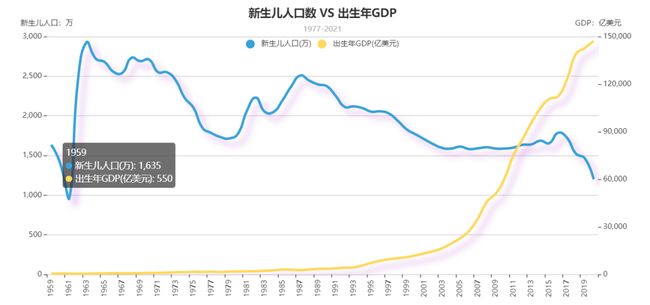
本文采用的数据来自世界银行官网（https://data.worldbank.org.cn/）的中国宏观经济数据集，现行版本的数据集共 45行12列，提供自1959年至2021年中国大陆12个指标每年的位置和数值。数据集格式采用国际通用惯例，每年的记录包含数值记录和比率记录，记录包含了时间(世界时)、人口(万人)、金额(亿美元)、比例等指标，数据集的结构如表1所示，图1画出了中国1949至2021年间的5个指标关系密切程度的热力图。

表 1 世界银行数据列表（↔️滑动查看更多）

出生年	高考年	新生儿人口（单位：万人）	大学招生扩招政策，布尔变量，0表示无，1表示是	出生年GDP（亿美元）	高考年GDP（亿美元）	高考年GDP占世界比例(%)	参加高考人数（单位：万人）	高考录取人数（单位：万人）	高考录取率	高等教育毛入学率	参加高考人数同比增长
1959	1977	1635	0	550	1749.4	2.39	570	27	4.74	1.65	NaN
1960	1978	1402	0	597.2	1495.4	1.73	610	40.2	6.59	2.87	0.07
1961	1979	949	0	500.6	1782.8	2.23	468	28	5.98	2.95	-0.233
1962	1980	2451	0	472.1	1911.5	2.12	333	28	8.41	1.14	-0.288
1963	1981	2934	0	507.1	1958.7	1.67	259	28	10.81	0.95	-0.222

图1 相关性热力图

02 统计分析

在1959年~2020年的61年间，新生儿数量有较大波动，1987年后新生儿数量呈单调递减趋势，且2016年后下降最为明显。

年GDP方面，呈上升趋势，1993年后变化较为明显。

整体上新生儿数量与出生年GDP无较为明显的关系，但存在部分区间负相关关系（1987年后）。

图2 人口趋势图

高考录取率与当年GDP如图3。两者均整体呈上升趋势，初步判断两者之间存在正相关关系。

图3 高考年录取率与GDP图

高考参加人数及与之相关的情况：参加高考的人数逐年增加，但是参加高考的人数的年同比增长变化波动大，无明显特征，如图4。

图4 高考录取人数详情图

观察高等教育毛入学率及当年GDP全球占比可知如图5。

图5 中国教育毛入学率与GDP占比动态图

毛入学率与全球GDP占比呈上升趋势，初步判断两者间存在正相关关系。

03 时间序列预测高考录取率

在此处，我们应用ARIMA模型进行高考录取率预测

在应用ARIMA模型时需要先对观测序列进行平稳性以及白噪声检验，只有平稳非白噪声序列才具有观测价值，详细流程有：

3.1

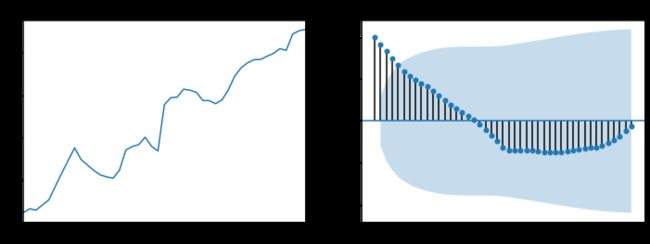
目标数据的原始数据序列时序图及自相关图

import matplotlib.pyplot as plt
# 确定目标数据
tag = data['高考录取率']
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(121)
tag.plot()
plt.title('Sequence diagram')
ax2 = fig.add_subplot(122)
plot_acf(tag,ax=ax2) # 自相关图
plt.show()

观察时序图可知：

由于该序列有明显的单调递增趋势，初步判断其为非平稳序列，且自相关图显示自相关系数长期大于0，说明序列间有很强的长期相关性。

结合上述流程，需要先对该序列进行平稳性检验。

3.2 ADF检验（单位根检验）

# 平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
ADF(tag)

(-0.5482617125015317,
 0.882249553115714,
 0,
 44,
 {'1%': -3.5885733964124715,
  '5%': -2.929885661157025,
  '10%': -2.6031845661157025},
 203.98252176030874)

观察结果，P值为0.882249553115714，显著大于0.05。

最终将该序列判断为非平稳序列。

由于最终判断该序列为非平稳序列，因此需要对其进行差分处理。

3.3 差分处理

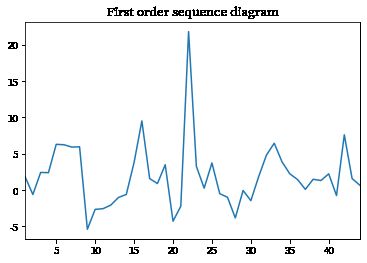
tag_diff = tag.diff().dropna()
tag_diff.plot()
plt.title('First order sequence diagram')
plt.show()  

从上图可以看出，一阶差分后的数据增减趋势较为平稳。但是依据最优化及准确性原则，需要再进行二阶差分处理。

## 二阶
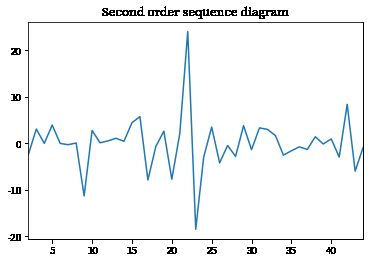
tag_diff2 = tag_diff.diff().dropna()
tag_diff2.plot()
plt.title('Second order sequence diagram')
plt.show()

理论上说，多阶的差分可以更好的剔除序列中的不确定因素，

但是差分的同时也会使得原序列损失一定的数据，所以差分的阶数应该适当。

在本文中，二阶差分过后，序列趋势较为平稳，接下来对二阶差分后的序列进行自相关及偏自相关图的绘制分析。

# 偏自相关
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(121)
plot_acf(tag_diff,ax=ax1)
ax2 = fig.add_subplot(122)
plot_pacf(tag_diff,ax=ax2)
plt.show()

ADF(tag_diff2)

(-7.7836768644929695,
 8.2881029271227e-12,
 1,
 41,
 {'1%': -3.60098336718852,
  '5%': -2.9351348158036012,
  '10%': -2.6059629803688282},
 202.9415785772855)

观察两图结果，

结果显示，二阶差分之后序列的自相关图有较强的短期相关性，且 ADF 检验中 p值为 8.2881029271227e-12，显著小于0.05，所以二阶差分后的序列是平稳序列。

结合流程图，平稳性检验后进行白噪声检验。

3.4 白噪声检验

检验结果如下

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(tag_diff2,lags=[6,12,24])

(array([14.16785, 16.24145, 22.69118]),
 array([0.02781, 0.18042, 0.53808]))

lbvalue: QLB检验统计量
pvalue: QLB检验统计量下对应的P值

此时查看P值，也就是第二行数据（各列分别为延迟6、12、24阶时的检验结果）：

当 lags=6 时，也就是延迟 6阶时 P值为 0.02781636 < 0.05，此时可判断该序列为非白噪声序列，具有观测价值。

3.5 应用ARIMA模型

from statsmodels.tsa.arima_model import ARIMA
# 一般阶数不超过length/10
pmax = int(len(tag_diff)/10)
qmax = int(len(tag_diff)/10)
bic_matrix = []

for p in range(pmax+1):
   tmp = []

for q in range(qmax+1):
   try:
       tmp.append(ARIMA(tag, (p,1,q)).fit().bic)
   except:
       tmp.append(None)
   bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)
p,q = bic_matrix.stack().idxmin()  ## 得到最小p、q值
## 由于对原视数据进行了二阶差分，所以此处的d值为 2
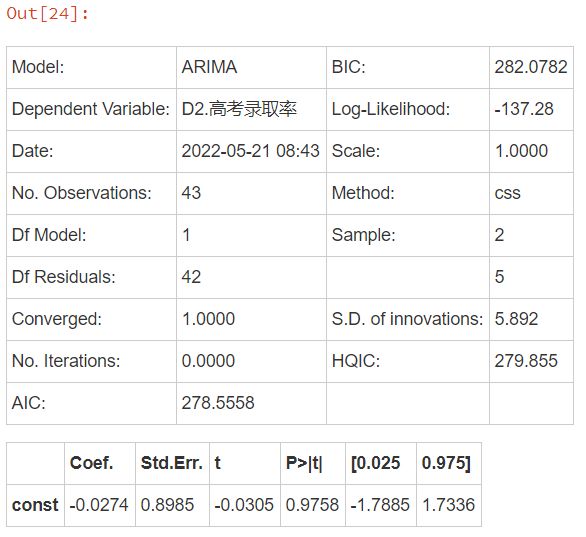
model = ARIMA(tag, (p,2,q)).fit() 
model.summary2()

预测2030年的高考录取率

print('预测2030年的高考录取率为 ' + 
      str(model.forecast(9)[0][-1]) + '%')

预测2030年的高考录取率为 95.79511627906977%

print('预测2030年的高考录取率为 ' + 
      str(model.forecast(9)[0][-1]) + '%')

预测2050年的高考录取率为 98.79511627906977%

04 结论

ARIMA是一种非常流行的时间序列统计方法，它是差分整合移动平均自回归模型，分别是自回归（AR）项指的是差分序列的滞后，移动平均（MA）项是指误差的滞后，而I是用于使时间序列平稳的差分数，描述了数据点的相关性，并考虑数值之间的差异。

本文借助ARIMA模型，通过对中国的往年高考录取率进行建模和预测，并验证和检验模型精度和可行性，来应用模型来估计未来的录取率，进一步得出了2030年中国高考录取率的预测值为 95.795%。（仅供学习参考）

采用差分整合移动平均自回归模型挖掘影响高考录取率的关键因素，然而差分整合移动平均自回归模型需要各指标与高考的相关关系，故可采用相关系数R的性质，得出各指标的相关性，建立ARIMA模型需要先对观测序列进行平稳性以及白噪声检验，只有平稳非白噪声序列才具有观测价值，最终预测高考录取率。

技术交流

目前开通了技术交流群，群友已超过3000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

方式①、发送如下图片至微信，长按识别，后台回复：加群；
方式②、添加微信号：dkl88191，备注：来自CSDN
方式③、微信搜索公众号：Python学习与数据挖掘，后台回复：加群