LeetCode | 图

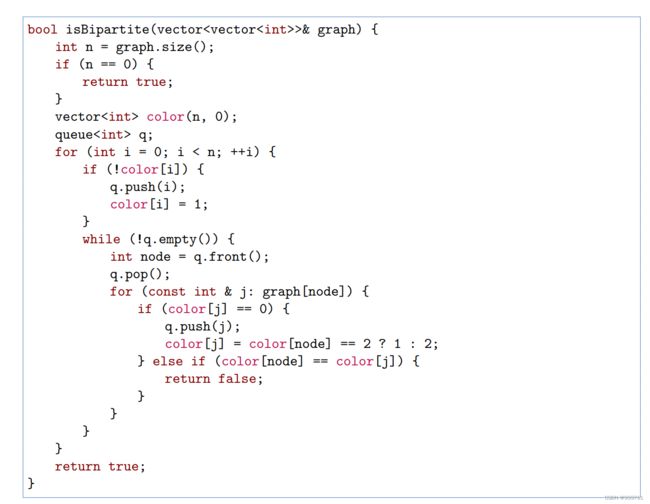
785. Is Graph Bipartite? （判断二分图）

• 思路：染色算法
  我们用 0 表示未检查的节点，用 1 和 2 表示两种不同的颜色。由于二分图的性质，连边的两个点必然染不同的颜色，所以从0开始，给他染颜色1，然后给邻点染颜色2，在从邻点遍历，染不同的染色。如果出现邻点与这个点有相同颜色，就不是二分图，false。
  

• 深度搜索
  注意：图中可能含有多个连通域，所以我们需要判断是否存在顶点未被访问，若存在则从它开始再进行一轮 dfs 染色。

具体：在cur顶点时，遍历所有邻点，如果邻点颜色与cur相同，矛盾返回false。如果邻点未被染色，则把这个点染成与cur不同的，再遍历这个邻点的邻点。

注意，需要遍历完所有cur的邻点才能得出cur与他邻点是否不同色的结论，即我们需要引入一个flag变量，如果仅仅找到一个未染色点，然后判断周围点的颜色，再看返回值，这个返回值作为Cur这个节点的返回值，这样是过于简单的，因为可能还存在其他未染色节点。

class Solution {
    public boolean isBipartite(int[][] graph) {
        ArrayList<ArrayList> res = new ArrayList<>();
        int[] visited = new int[graph.length];

        boolean ans = true;
        //注意：可能有多个连通分支，对每个连通分支遍历是否为二分图
        for (int i = 0; i < graph.length; i++) {
            if (visited[i] == 0) {
                visited[i] = 1;
                ans = ans &&dfs(graph,visited,i);
            }
        }
        return ans;
    }
    
    boolean dfs(int[][] graph, int[] visted, int cur){

        int c = visted[cur];
        boolean flag = true;
        for(int j=0; j<graph[cur].length;j++){
            if(visted[graph[cur][j]]==c) return false;
            if(visted[graph[cur][j]]==0) {
                visted[graph[cur][j]]= c==1? 2:1;
                flag &= dfs(graph,visted,graph[cur][j]);
            }
        }
        return flag;
    }
}

• 广度优先搜索

也就是先搜0这个点的所有邻点，放入栈中，把邻点染成与0这个点不同的颜色，然后再遍历0的邻点的邻点，依次类推

210. Course Schedule II （课程表II）

• 具体思路

首先，建立有向图，[a,b]表示修a前要先修b，这时我们要让b指向a，把b加入a的列表中。拿prerequisites = [[1,0],[2,0],[3,1],[3,2]]举例，我们建立的list列表edges就为[ [ ], [0], [0], [1,2]]，表示修0的时候不用修别的，修1的时候要修0，修2的时候要修0，修3的时候要修1和2

接着，我们建立indeg表示每门课的先修课程数目（即入度），则indeg=[0,1,1,2]

其次，我们找到入度为0的点课0，把他加入队列，然后遍历有向图edges，把有先修0的课程入度减1，如果这时候有课程入度变为0，即说明前面的已经先修完了，所以可以加入队列，然后再遍历先修课为这门新入度为0的课的，入度再减去一

class Solution {
    // 存储有向图
    List<List<Integer>> edges;
    // 存储每个节点的入度
    int[] indeg;
    // 存储答案
    int[] result;
    // 答案下标
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < numCourses; ++i) {
            edges.add(new ArrayList<Integer>());
        }
        indeg = new int[numCourses];
        result = new int[numCourses];
        index = 0;
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
            ++indeg[info[0]];
        }

        Queue<Integer> queue = new LinkedList<Integer>();
        // 将所有入度为 0 的节点放入队列中
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }

        while (!queue.isEmpty()) {
            // 从队首取出一个节点
            int u = queue.poll();
            // 放入答案中
            result[index++] = u;
            for (int v: edges.get(u)) {
                --indeg[v];
                // 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if (indeg[v] == 0) {
                    queue.offer(v);
                }
            }
        }

        if (index != numCourses) {
            return new int[0];
        }
        return result;
    }
}

Python版本：

class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        dic = {}
        inp = {}
        res = []
        s = set()

        # 每个点对应的先修map
        for i in range(len(prerequisites)):
            edge = prerequisites[i]
            if edge[0] not in dic.keys():
                dic[edge[0]] = [edge[1]]
            else:
                dic[edge[0]].append(edge[1])
        
        for key in dic.keys():
            inp[key] = len(dic[key])
        
        # 队列遍历
        stack = []
        for i in range(numCourses):
            if i  not in dic.keys():
                stack.append(i)
        while(len(stack)>0):
            
            cur  = stack.pop(0)
            res.append(cur)
            s.add(cur)
            
            for key in dic.keys():
                if cur in dic[key]:
                    inp[key] -= 1
                if inp[key]==0 and key not in s:
                    
                    s.add(key)
                    stack.append(key)
        
        if len(res)!=numCourses:
            return []
        else:
            return res

1059. All Paths from Source Lead to Destination (Medium)

判断是否所有路径都能从source到Destination ，是的话返回true

输入：n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
输出：false
说明：节点 1 和节点 2 都可以到达，但也会卡在那里。

注意判断是否陷入了环路。

具体做法：

1. 首先，建立vistied列表，记录是否遍历过。并建立m表，记录每个点指向的下一个点是什么。例如edges = [[0,1],[0,2]]，则m=[ [1,2], [ ], [ ] ]，如果destination 还会指向下一个点，则返回False

2. 接着，dfs遍历。遍历到cur时，如果cur没有下一个点，且cur不是终点则返回false；否则，for循环遍历cur的下一个点，如果下个点访问过了，则返回false（因为有环），没遍历过，则标记为遍历了，然后看下一个点能否走到终点。最后再回溯，再遍历另外的下一个点

class Solution {
public:
    bool leadsToDestination(int n, vector<vector<int>>& edges, int source, int destination) {
    	vector<bool> visited(n, false);
    	vector<vector<int>> m(n);
    	for(auto& e : edges)
    		m[e[0]].push_back(e[1]);
    	if(!m[destination].empty())
    		return false;//终点后面还有路径
		return dfs(m,visited,source,destination);
    }
    bool dfs(vector<vector<int>>& m, vector<bool>& visited, int cur, int destination) 
    {
    	if(m[cur].size()==0 && cur != destination)
    		return false;//到达一个终点，但不是目标点
    	for(int next : m[cur])//往下走
    	{
    		if(visited[next])//访问过了
    			return false;//有环
    		visited[next] = true;//访问
    		if(!dfs(m, visited, next, destination))
    			return false;
    		visited[next] = false;//回溯
    	}
        return true;
    }
};

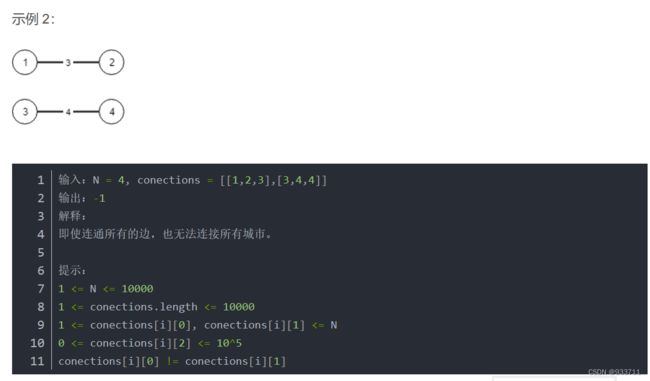
1135. Connecting Cities With Minimum Cost 最小生成树

每个城市之间的连接有费用，现在返回连通所有城市的最小费用，如果非连通图，可以返回-1

有两种算法，一个是Kruskal，一个是Prim

• Kruskal算法
  将边的权值排序，小的先遍历，用并查集检查两个顶点是否合并了，没有合并则将该边加入生成树
  PS：也可以使用优先队列实现（相当于排序）

具体做法：

class Solution {
public:
    int find(int x) //不断向上找，直到找到下标和元素相同的点；不理解背后原因的，可以学习下树的数组表示发。
    {
        while(x != p[x]) x = p[x];
        return x;
    }
    int minimumCost(int N, vector<vector<int>>& connections) {
        int ans = 0;
        int point_num = 0;
        //sort重定义比较是重载的<号，为真则不交换，否则交换。
       //基于上述原则，对cmp返回对应的true or false
        auto cmp = [](vector<int> &a,  vector<int> &b){return a[2] < b[2];};
        for(int i = 0; i <= N; i++) {
            p.push_back(i);
        }
        sort(connections.begin(), connections.end(), cmp);//按cost值排序，采用贪心算法
        for (auto conn : connections) {
            int px = find(conn[0]),py = find(conn[1]);
            if(px != py) { //如果该边所在的两个节点不在同一个集合
                p[px] = py; //合并集合
                ans += conn[2];
                point_num++;
                //对于无向图的话，至少需要n-1条边可以使得图是联通的；
                //如果对于有向图的话，至少需要n条边才可以使得图是联通的
                if(point_num == N - 1){  
                    return ans;
                } 
            } 
        }
        return -1;
    }
private:
    vector<int> p; //集合关系表，用一个数组来描述N个节点的集合关系；等同于树的数组表示方法。
};

• prim算法
  prim算法核心思想
  1）以某一个点为起点（通常为数组的第一个点）。以“点”为参照物，从该点所在“集合”的边当中依次选择cost最小的边去连接一个“新的”节点。
  2）在一个结合新（要注意是新的，否则会死循环）加入一个节点后，将会扩大原有的集合，而该集合所连接的边和点都会发生变化。针对这类问题，选择小顶堆作为数据结构。
  3）当该集合中有N个点时，所有的点都已经被访问过了。

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& connections) {
        //重载priority_queue的比较函数，priority_queue默认是大顶堆，重载的是<号
        //默认情况下如果左边参数大于右边参数，则说明左边形参的优先级低于右边形参，会将左边的放到后面
        //构建小顶堆时，我们实现一个>号的判断即可，大于返回true，优先级低，被放到后面，则小的会放前面
        struct cmp {
            bool operator () (const vector<int> &a, const vector<int> &b) {
                return a[2] > b[2];
            }
        };
        int selected = 0, ans = 0;
        //构建点和cost的集合关系，本质是个三维数组，第一维是起点，二维是<终点、开销>
        vector<vector<pair<int,int>>> edgs(N+1,vector<pair<int,int>>());
        //构建小顶堆，将最合适的点放在最前面
        priority_queue<vector<int>,vector<vector<int>>,cmp> pq;
        vector<int> visit(N+1, 0);
        //初始化边集合
        for(auto re : connections){
            edgs[re[0]].push_back(make_pair(re[1],re[2]));
            edgs[re[1]].push_back(make_pair(re[0],re[2]));
        }
        //本次选择1为起点，如果1点没有变，则1永远是孤岛。本次选择1为起点
        if(edgs[1].size() == 0){
            return -1;
        }

        selected = 1;
        visit[1] = true;
        //起点1所在的边放入小顶堆
        for(int i = 0;i < edgs[1].size(); ++i){
            pq.push(vector<int>({1,edgs[1][i].first,edgs[1][i].second}));
        }
       //遍历小顶堆
        while(!pq.empty()) {
            auto curr = pq.top();pq.pop();
            if(!visit[curr[1]]){
                visit[curr[1]] = true;
                ans += curr[2];
                 //依次取出cost最小的边所在的点加入集合
                for(auto e : edgs[curr[1]]){
                    pq.push(vector<int>({curr[1],e.first,e.second}));
                }
                selected++;
                if(selected == N){ //如果N个节点都在时，则结束循环
                    return ans;
                }
            }
        }
        return -1;
    }
};