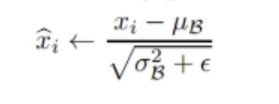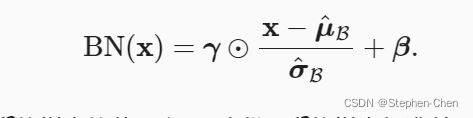【深度学习理论】之Batch Normalization(BN层)
参考:BN层
一、背景
引入原因
随着网络越深,在反向传播算法向后传播的时候,梯度不断的相乘,从前到后之后,梯度将会很小
损失出现在最后,后面的层训练的较快
而数据在最底部
底部的层训练较慢
底部层一变化,所有都跟着变化
最后那些层需要重新学习多次
导致收敛变慢
因此:可以在学习底部层的时候避免变化的顶不层
提出
2015 年,Google 研究人员Sergey Ioffe等提出了一种参数标准化(Normalize)的手段,并基于参数标准化设计了 Batch Nomalization(简称 BatchNorm或 BN)层 。BN层提出后:
- 使得网络的超参数的设定更加自由,比如更大的学习率,更随意的网络初始化等,同时网络的收敛速度更快,性能也更好。
- 广泛地应用在各种深度网络模型上,卷积层、BN 层,ReLU 层、池化层一度成为网络模型的标配单元,堆叠 方式Conv-BN-ReLU-Pooling 。
- 正则化可以防止过拟合现象
- 在残差块提出后,批量规范化使得研究人员能够训练100层以上的网络。
#BN层的位置 Conv BN ReLU Pooling
二、理论
网络层的输入x分布相近,并且分布在较小范围内时(如 0-1),更有利于函数的迭代优化。
通过数据标准化操作可以将数据x映射成
,对每个Batch(一批)进行规范化,规范化的公式如下:
公式中的含义:
常量ϵ>0,以确保不会除以零,即使在经验方差估计值可能消失的情况下也是如此
总结:
上面的公式表示的是正太分布。也就是说,通过上面的公式计算,可以将原本随机分布的输入数据x,转化成按正太分布分布的数据
从而使得输入网络的数据分布较近,有利于网络的迭代优
批量规范化BN公式:“scale and shift”技巧
最初论文是想用它来减少内部协变量的转移
后续有指出可能就是通过在每个小批量里加入噪音来控制模型的复杂度
γ参数实现对标准化后的
再次进行缩放,
β参数实现对标准化的
进行平移
三、网络层应用
全连接层(Linear)后的BN层
BN层置于全连接层中的仿射变换和激活函数之间
- 全连接层的输入为u,
- 权重参数和偏置参数分别为W和b,
- 激活函数为ϕ,
- 批量规范化的运算符为BN。
卷积层后的BN层
在卷积层之后和非线性激活函数之前应用BN
预测过程中的BN层
BN层在训练模式和预测模式下的行为通常不同:
- 测试不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差。
- 其次,需要使用我们的模型对逐个样本进行预测。 常用的方法是通过移动平均估算整个训练数据集的样本均值和方差,并在预测时使用它们得到确定的输出。
和dropout一样,BN层在训练模式和预测模式下的计算结果也是不一样的。
model.train()和model.eval()
三、代码实现
定义bn公式 :
import torch
from torch import nn
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4) #这是一个元组
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.dataBatchNorm层
class BatchNorm(nn.Module):
# num_features:完全连接层的输出数量或卷积层的输出通道数。
# num_dims:2表示完全连接层,4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 非模型参数的变量初始化为0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果X不在内存上,将moving_mean和moving_var
# 复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y使用BN层
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
nn.Linear(84, 10))四、总结
- 批量归一化固定小批量中的均值和方差,然后学习出适合的偏移和缩放
- 可以加速收敛速度,但一般不改变模型精度
- 使用BN时需要注意的问题:
- 训练时要将traning参数设置为True,在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
batch size尽可能设置大点,设置小后表现可能很糟糕,设置的越大求的均值和方差越接近整个训练集的均值和方差。
建议将bn层放在卷积层(Conv)和激活层(例如Relu)之间,且卷积层不要使用偏置bias,因为没有用,参考下图推理,即使使用了偏置bias求出的结果也是一样的