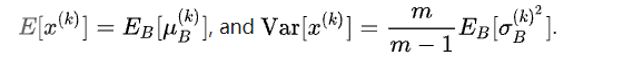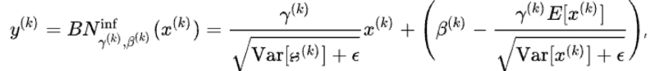Batch Normalization

首先推荐旷世的视频：https://www.bilibili.com/video/BV1DM4y1w7J4?p=1&share_medium=iphone&share_plat=ios&share_source=COPY&share_tag=s_i×tamp=1640004017&unique_k=Uzf93PU

【manim】5 分钟理解 BatchNorm

BN 添加位置

全连接层：添加在每一个全连接和激活函数之间；

卷积神经：卷积计算之后、激活函数之前；

计算公式

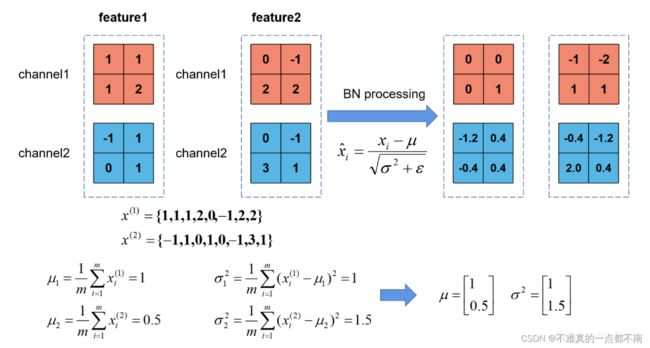
对于一个拥有$d$维的输入$x$，我们将对它的每一个维度进行标准化处理。

对于一个RGB图像，这里的$d$指的是channels=3 $x=(x^{(1)},x^{(2)},x^{(3)})$

BN分别对每个channel进行Normalization。

下标1,2,3…,m表示样本维度，上标(1),(2)…,(c )表示channel 维度。

训练

Input：a mini-batch with m个样本:$B=(x_1,...,x_m)\in {\mathbb{R}}^{m\times c\times H\times W}$其中$x_i=(x_i^{(1)},...,x_i^{(c)})$
需要学习的量： $\gamma$——BN的weight 、 $\beta$——BN的bias

前向传播

input mean:$\frac{1}{m}{\sum }_{i=1}^m{x}_i\to {\mu }_B=({\mu }_B^{(1)},...,{\mu }_B^{(c)})\in {\mathbb{R}}^{c\times 1}$

例${\mu }_B^{(1)}=\frac{1}{m}{\sum }_{i=1}^m{x}_i^{(1)}=\frac{1}{mHW}{\sum }_{i=1}^m{\sum }_{j=1}^H{\sum }_{k=1}^W{x}_i^{(1)(j)(k)}$

同理 input var: $\frac{1}{m}{\sum }_{i=1}^m(x_i-{\mu }_B{)}^2\to {\sigma }_B^2\in {\mathbb{R}}^{c\times 1}$

更新后的值：${\hat{x}}_i=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B+ϵ}}$

Output:$y_i=\gamma {\hat{x}}_i+\beta$

可以看下面这个例子加深理解：

反向传播

根据最终的输出结果更新$\gamma 、\beta$

推理

训练与推理时BN中的均值、方差分别是什么？

训练时，均值、方差分别是该batch内数据相应维度的均值与方差；

推理时，均值、方差是基于所有batch的期望计算所得，公式如下：

Pytorch中的Batch Norm

PyTorch 源码解读之 BN & SyncBhttps://zhuanlan.zhihu.com/p/337732517
详情可看上面，这里先不写了。
原论文中并没有running statistics 的概念。
Pytorch这里用到EMA update：

running statistics ${\hat{x}}_{\text{new}}=(1-\text{momentum})\times \hat{x}+\text{momentum}\times x_t$

$\hat{x}$ is the estimated statistic and $x_t$is the new observed value

$\hat{x}$: running _mean 、running_var

$x_t$: input_mean、input_var

训练完毕后保留 $\gamma$、$\beta$、running _mean 、running_var。

验证时：$y=\frac{\gamma }{\sqrt{running-var}+ϵ}x+(\beta -\frac{\gamma }{\sqrt{running-var}+ϵ}runing-mean)$