MOCO论文精读-用于组合优化的机器学习：方法论之旅(Yoshua Bengio, 2021)-翻译

Machine learning for combinatorial optimization: A methodological tour d’horizon

论文：Bengio Y, Lodi A, Prouvost A. Machine learning for combinatorial optimization: a methodological tour d’horizon[J]. European Journal of Operational Research, 2021, 290(2): 405-421.

链接：https://doi.org/10.1016/j.ejor.2020.07.063

本文篇幅很长(不算参考文献也有15页)，为方便以后的回顾，本博文主要是对该文的一个翻译，可能有的地方翻译、解释的不准确，还请见谅。

作者介绍

Yoshua Bengio(约书亚·本吉奥)：2018年图灵奖得主、加拿大蒙特利尔大学教授，谷歌学术被引49w+，与Geoffrey Hinton(被引54w+)以及Yann LeCun(被引23w+)称为深度学习三巨头，并一同获得2018年图灵奖，Hinton、Bengio、LeCun都是深度学习领域的先行者。

深度学习三巨头，从左到右依次是LeCun、Hinton、Bengio

本人研究方向

硕士期间：机器学习及智能系统开发——致力于使用包括深度学习、强化学习在内的机器学习算法解决现存实际问题，如污水处理的水质预测以及智能控制、建筑文本分析以及智能上肢康复系统的开发；

博士期间：多目标组合优化与决策研究——致力于多约束多目标多任务组合优化算法和多目标决策系统的研究与开发，以及多目标优化技术在一些工程实践中的应用。

名词介绍

operation research(OR)：运筹学

摘要

本文调查了最近的尝试,从机器学习和运筹学的社区,在利用机器学习来解决组合优化问题。考虑到这些问题的本质,最先进的算法依赖手工制作的启发式决策,否则计算或数学不定义良好的成本太高。因此,机器学习看起来像一个自然的候选人做出这样的决策原则和优化方法。我们倡导推动进一步一体化的机器学习和组合优化和细节的方法。论文的主要观点是认为通用的优化问题是数据和查询是什么问题用于学习的相关分布在一个给定的任务。

---

---

1 引言

运筹学(operation research, OR)，也称为规范分析，始于第二次世界大战，作为一项使用数学和计算机科学来帮助军事规划者做出决策的倡议。 如今，它被广泛应用于行业，包括但不限于交通、供应链、能源、金融、调度等。 在这篇论文中，我们关注的是离散优化问题，它被表述为整数约束优化，即具有整数或二元变量（称为决策变量）。虽然并非所有此类问题都难以解决（例如，最短路径问题），但我们专注于组合优化问题（NP-hard）。这是个坏消息，因为对于这些问题，不太可能存在运行时间与输入大小成多项式的算法。然而，在实践中，组合优化算法可以解决多达数百万个决策变量和约束的实例。

本文的重点是组合优化算法，该算法自动对选定的隐式问题分布进行学习。 在算法中加入机器学习组件可以实现这一点。机器学习侧重于在给定一些（有限且通常有噪声的）数据的情况下执行任务。它非常适合于没有明确的数学公式的自然信号，因为真正的数据分布在分析上是未知的，例如在处理图像、文本、声音或分子时，或者在使用推荐系统、社交网络或财务预测时。大多数情况下，学习问题有一个统计公式，通过数学优化来解决。近年来，机器学习子领域通过构造更简单的函数来构建大参数近似器，这一研究取得了巨大的进展。深度学习在具有大量数据点的高维空间中应用非常出色。

1.1 动机

从组合优化的角度来看，机器学习可以从两个方面改进问题实例分布的算法：

• 一方面，研究者假设了关于优化算法的专家知识，但希望用快速近似来代替一些繁重的计算。学习可以用来以一般的方式建立这样的近似，即无需导出新的显式算法。
• 另一方面，专家知识可能不够充分，某些算法决策可能不尽如人意。

因此，我们的目标是探索这些决策的空间，并从这些经验中学习最好的表现行为（决策），希望在最新技术水平上有所改进。尽管机器学习是近似的，但我们将通过本文所调查的例子来证明，这并不系统地意味着整合学习将损害总体理论保证。从使用机器学习来处理组合问题的角度来看，组合优化可以将问题分解为更小的、希望更简单的学习任务。因此，组合优化结构作为模型的相关先验。这也是利用组合优化文献的机会，特别是在理论保证方面（例如，可行性和最优性）。

1.2 研究背景

比如旅行商问题(Traveling Salesman Problem, TSP)。公司不关心解决所有可能的旅行推销员问题，而只关心他们的问题。明确定义使旅行推销员问题成为公司可能的问题是乏味的、不可扩展的，并且在明确编写优化算法时如何利用它还不清楚。我们想自动专为这个公司的旅行推销员问题算法。场景中可能的旅行商问题的真实概率分布定义了我们希望算法在哪些实例上表现良好。 这是未知的，甚至无法以明确的方式在数学上进行表征。 因为我们不知道这个分布中有什么，我们只能学习一个算法，该算法在从这个分布中采样的有限旅行商问题集（例如，公司收集的一组历史实例）上表现良好，从而隐含地结合 有关实例分布的所需信息。

作为比较，在传统的机器学习任务中，真实分布可能是猫的所有可能图像的分布，而训练分布是此类图像的有限集合。 学习的挑战在于，在用于学习的问题实例上表现良好的算法可能无法在真实概率分布中的其他实例上正常工作。 对于公司来说，这意味着该算法只在过去的问题上表现良好，而在未来的问题上表现不佳。 为了控制这一点，我们监督学习算法在另一组独立的未见问题实例上的性能。 保持用于学习的实例和未见过的实例之间的性能相似在机器学习中称为泛化。 当前的机器学习算法可以泛化到来自相同分布的示例，但往往更难以泛化分布外的示例（尽管这是 ML 中深入研究的主题），因此我们可以认为利用机器学习的组合优化算法 在与用于训练机器学习预测器的情况相差太远的未见问题实例上进行评估时，模型会失败。如前所述，同样值得注意的是，传统的组合优化算法甚至可能无法在问题的所有可能实例中始终如一地工作，而是倾向于更适应特定的问题结构，例如 , 欧几里得旅行商问题。

最后，机器学习算法提取的隐性知识与通过组合优化研究提取的来之不易的显性专业知识相辅相成。 相反，它旨在增强和自动化各种现有算法的不成文的专家直觉（或缺乏）。 鉴于这些问题是高度结构化的，我们认为通过机器学习来增强求解算法是相关的——尤其是深度学习来解决这些问题的高维。

在下文中，我们调查了文献中实现这种自动化和增强的尝试，并对这些方法进行了方法论概述。鉴于该领域的现状，我们调查的文献是探索性的，也就是说，我们的目标是强调在组合优化中使用机器学习的前景研究方向，而不是报告已经成熟的算法。

1.3 论文结构

我们介绍了与机器学习一起构建组合优化算法的背景和动机。 本文的其余部分安排如下。 第 2 章提供了充分掌握论文内容所必需的组合优化、机器学习、深度学习和强化学习的最低先决条件。 第 3 章回顾了最近的文献，并得出了两个独特的正交观点：第 3.1 节展示了机器学习策略如何可以通过模仿专家来学习或通过经验发现，而第 3.2 节讨论机器学习和组合优化组件之间的相互作用。 第 5 章进一步推动了对使用机器学习进行组合优化的反思，并提出了一些方法论点。 在第 6 章中，我们详细介绍了该领域的关键实际挑战。 最后，在第 7 章中得出了一些结论。

2 前期知识准备

在本节中，我们给出了组合优化和机器学习的基本（有时是粗略的）概述，其独特目的是介绍理解本文其余部分所必需的概念。

2.1 组合优化

在不丧失通用性的情况下，组合优化问题可以表示为约束最小优化问题。约束模型是问题的自然或强加的约束，变量定义了决策，而目标函数(通常是最小化的成本)定义了变量值的每一个可行赋值的质量度量。如果目标和约束是线性的，则该问题称为线性规划问题。此外，如果某些变量也被限制为仅假设整数值，则该问题是混合整数线性规划问题(mixed-integer linear programming problem)。

满足约束的点集就是可行域。该集合中的每个点（通常称为可行解）都会产生最优解的目标值的上限。精确求解是该领域的一个重要方面，因此也非常关注寻找最低成本的下限。就最优解值而言，下界越紧，解决下面描述的混合整数线性规划的当前算法方法成功的机会就越高，即，即使不是真有效的，也被认为是有效的。

线性和混合整数线性规划问题是组合优化的主力，因为它们可以对各种各样的问题进行建模并且是最容易理解的，即有可靠的算法和软件工具来解决它们。 我们在本文中对它们进行了特殊考虑，但当然，它们并不代表整个组合优化，混合整数非线性规划在理论和实际应用中都是一个快速扩展且非常重要的领域。 关于复杂度和求解方法，线性规划是一个多项式问题，通过单纯形算法或内点法在理论上和实践中都得到了很好的解决。 另一方面，混合整数线性规划是一个 NP-hard 问题，这并不意味着它没有希望。 实际上，很容易看出混合整数线性规划的复杂性与（某些）变量的完整性要求相关，这使得混合整数线性规划的可行域是非凸的。 然而，放弃完整性要求 (i) 定义了混合整数线性规划的适当松弛（即，其可行区域包含混合整数线性规划可行区域的优化问题），其中 (ii) 恰好是线性规划， 即，多项式可解。 这立即暗示了用于通过分支限界技术的整个生态系统来解决混合整数线性规划的算法攻击线，以执行隐式枚举。

分支限界实现了一种由搜索树表示的分而治之的算法，其中在每个节点处，问题的线性规划松弛（可能通过分支决策增强，见下文）被有效地计算。 如果松弛不可行，或者松弛的解自然是（混合）整数，即混合整数线性规划可行，则不需要扩展节点。 否则，在那些应该是整数的变量中，至少存在一个变量，在线性规划解决方案中取小数值，并且可以选择该变量进行分支（枚举），即通过限制其值的方式使得两个子节点被创建。 两个子节点有不相交的可行域，都不包含之前线性规划松弛的解。 我们使用图 1 来说明最小化混合整数线性规划的分支限界算法。 在图中的根节点处，变量 $x_2$ 在线性规划解中具有一个小数值（未表示），因此在该值的底部（此处为 0）和天花板（此处为 1）上进行了分支。 当找到整数解时，我们还会得到问题最优解值的上限（表示为$z$ ）。 在每个节点上，我们可以将松弛的解值（表示为 $z$ ）与目前找到的最小上限（称为现有解值）进行比较。 如果对于特定节点，后者小于前者，则在该节点本身产生的子树中找不到更好的（混合）整数解，可以对其进行剪枝。

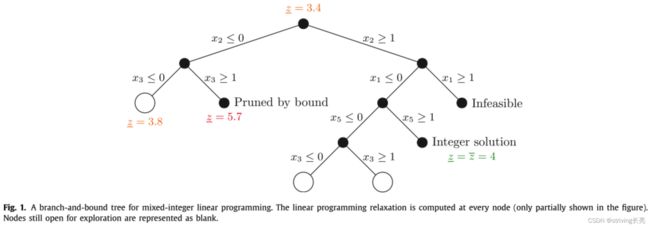
图解释：用于混合整数线性规划的分支定界树。 在每个节点处计算线性规划松弛（图中仅部分显示）。 仍然开放供探索的节点表示为空白。

所有商业和非商业混合整数线性规划求解器都通过广泛使用切割平面来增强上述枚举框架，即添加到原始公式中的有效线性不等式（尤其是在分支限界树的根部） 加强其线性规划松弛的尝试。 由此产生的框架，称为分支和切割算法，然后通过额外的算法组件进一步增强，预处理和原始启发式是最关键的。

最后，我们注意到有大量文献致力于（原始）启发式算法，即设计用于在没有最优性保证的情况下计算组合优化问题的“实践中良好”解决方案的算法。 尽管对它们的一般性讨论超出了本文的范围，但这些启发式方法在组合优化中起着核心作用，并将在本文的特定上下文中进行考虑。

2.2 机器学习

2.2.1 监督学习

在监督学习中，提供了一组输入（特征）/目标对，任务是找到一个函数，该函数对于每个输入都有一个尽可能接近所提供目标的预测输出。 找到这样的函数称为学习，并通过一系列函数的优化问题来解决。 损失函数，即输出和目标之间差异的度量，可以根据任务（回归、分类等）和优化方法来选择。 但是，这种方法还不够，因为该问题具有统计性​​质。 在给定的例子上取得好成绩通常很容易，但人们希望在未见过的例子（测试数据）上取得好成绩。 这被称为泛化。

如果一个模型（即，一组函数）可以表示许多不同的函数，则该模型被认为具有高容量，并且首先是过拟合：在训练数据上做得好，但是不能推广到测试数据。正则化是以训练分数为代价来提高测试分数并用于限制模型的实际能力的任何事物。相反，如果容量太低，则模型在两组中都不适合并且性能不佳。过拟合和不拟合之间的界限可通过改变有效能力（通过训练可达到的函数族的丰富度）来估计：在临界能力以下，一个欠拟合和测试误差随能力的增加而减少，而在临界能力以上，一个过拟合和测试误差随能力的增加而增加。

无法在测试集上从各种经过训练的模型中选择最佳模型。选择是优化的一种形式。为了进行模型选择，需要使用验证数据集来估计不同机器学习模型的泛化误差。可以根据这些估计进行模型选择，并且可以在测试集上计算所选模型的最终无偏泛化误差。因此，验证集通常用于选择有效容量，例如，通过改变训练量、参数数量θ和施加给模型的正则化量。
（监督学习的有关知识在此不进行过多描述）

2.2.2 无监督学习

在无监督学习中，对于想要解决的任务没有目标，而是试图捕捉观察到的随机变量的联合分布的一些特征。 各种任务包括密度估计、降维和聚类。 因为到目前为止，无监督学习与组合优化结合起来很少受到关注，而且它的直接使用似乎很困难，所以我们不再进一步讨论它。

2.2.3 强化学习

与强化学习相关的马尔可夫决策过程。

注：代理行为由其策略$\pi$定义，而环境演化由动态$p$定义。注意，奖励不是定义进化所必需的，并且仅作为代理的学习机制提供。在一般框架中，动作、状态和奖励是随机变量。

在强化学习中，代理人(agent)通过马尔可夫决策过程与环境交互，如图 所示。在每个时间步，代理处于给定的环境状态，并根据其（可能是随机的）策略选择一个动作。结果，它从环境中获得奖励并进入新的状态。强化学习的目标是训练智能体最大化未来奖励的预期总和，称为回报。对于给定的策略，给定当前状态（分别是状态和动作对）的预期回报被称为价值函数（resp. state action value function）。值函数遵循贝尔曼方程，因此可以将问题表述为动态规划，并近似求解。代理不需要知道环境的动态，而是直接或间接地学习，从而产生探索与利用的两难境地：在探索新状态以提炼环境知识以实现可能的长期改进之间进行选择，或利用最知名的到目前为止学习的场景（往往处于已访问或可预测的状态）。

状态应该在每一步都充分表征环境，即未来状态仅通过当前状态（马尔可夫属性）依赖于过去状态。如果不是这种情况，可以应用类似的方法，但我们说代理接收状态的观察。马尔可夫性质不再成立，马尔可夫决策过程被认为是部分可观察的。定义奖励函数并不总是那么容易。有时想要定义一个非常稀疏的奖励，例如当智能体解决问题时为 1，否则为 0。由于其潜在的动态规划过程，强化学习自然能够将导致未来奖励的状态/行为归功于。尽管如此，上述设置具有挑战性，因为在代理（随机或通过高级方法）解决问题之前，它不提供学习机会。此外，当策略被近似时（例如，通过线性函数），学习不能保证收敛并且可能陷入局部最小值。例如，一辆自动驾驶汽车可能会因为害怕撞到行人而决定不去任何地方行驶并获得巨大的负面奖励。这些挑战与上述探索困境密切相关。

2.2.4 深度学习

包括反向传播、梯度下降、CNN、RNN等深度学习基础知识，在此不做过多叙述，有兴趣的可以查看Bengio原文或者博主AI浩在CSDN撰写的文章：五万字总结,深度学习基础。

在Bengio的介绍中，也介绍了Attention机制，在此也不做多过介绍，有兴趣的可以查看我之前的文章。

3 研究现状

我们调查了机器学习的不同用途，以帮助解决组合优化问题并沿两个正交轴组织它们。 首先，在第 3.1 节中，我们说明了使用学习的两个主要动机：近似和发现新策略。 然后，在第 3.2 节中，我们展示了结合学习和传统算法元素的不同方法的示例。

3.1 学习方法

本节涉及 1.1 节中报告的在组合优化中使用机器学习的两个动机。 在一些工作中，研究人员假设了有关为组合优化算法做出的决策的理论和/或经验知识，但希望通过使用机器学习来近似其中一些决策来减轻计算负担。 相反，我们也受到以下事实的激励：有时，专家知识并不令人满意，研究人员希望找到更好的决策方式。 因此，机器学习可以通过反复试验强化学习来训练模型。

我们在第 2.2 节介绍的状态/动作马尔可夫决策过程框架中构建了这两种动机，其中环境是算法的内部状态。我们关心组合优化算法使用的学习算法决策，我们将决策函数称为策略，即在给定所有可用信息的情况下(在Markov决策过程设置中，如果信息足够充分地表征当时的环境，则为一种状态)， 返回（可能是随机的）要采取的行动。策略是我们想要使用机器学习学习的功能，我们将在下面展示这两种动机如何自然地产生两种学习设置。请注意，马尔可夫决策过程的轨迹长度值为 1 的情况是一种常见的边缘情况（称为老虎机设置），在这种情况下，这种公式似乎有些过分，但它仍然有助于比较方法。在使用机器学习来近似决策的情况下，策略通常是通过模仿学习来学习的，这要归功于演示，因为预期的行为是由专家（也称为 oracle，即使它不一定是最优的），如图 所示。在这种情况下，学习者没有被训练来优化性能度量，而是盲目地模仿专家。

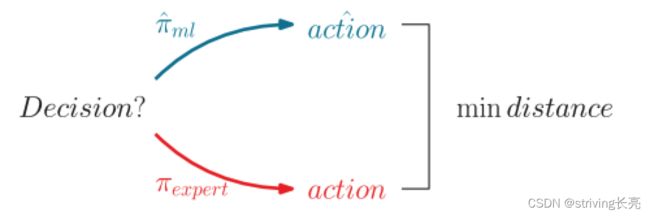
在演示环境中，通过最大限度地减少行动空间中的差异，对决策进行训练以再现专家决策的行动。

在注重发现新策略，即从头开始优化算法决策函数的情况下，可以通过经验的强化学习来学习策略，如图所示。尽管我们在强化学习的基本马尔可夫决策过程中提出了学习问题，但这并不限制我们使用主要的强化学习算法(近似动态规划和策略梯度)来最大化期望的回报之和。也可以使用诸如强盗算法、遗传算法、直接/局部搜索等备选优化方法来解决强化学习问题。一般来说，确定哪种算法表现最好是一个开放的研究问题，不太可能有一个简单的答案，并且超出了这里介绍的方法的范围。

通过奖励信号学习时，没有专家参与；只有最大化预期的未来回报（回报）才重要。

重要的是要理解，

• 在模仿的环境中，策略是通过专家为每个动作提供的监督目标学习的（没有奖励），在模仿学习中，代理被教导做什么，并按照专家指示进行操作。

• 而在体验的环境中，策略是通过强化学习（没有专家）从奖励（可能延迟）信号学习的。并且代理被鼓励快速积累奖励。

这两种设置之间的区别要比这里的区别复杂得多。我们将在第5.1节中探讨其中的一些复杂性，包括它们的优缺点。在下文中，很少有论文对不同的环境进行了调查。

3.1.1 Demonstration

通过演示学习政策与监督学习相同，即由专家提供输入状态和目标动作的培训对。在最简单的情况下，事先收集专家决策，但更先进的方法可以在线收集，以提高稳定性，

3.1.2 Experience

考虑到旅行推销员问题，很容易设计出一种贪婪启发式，该启发式通过在尚未访问的节点中依次选择节点来构建旅行，从而定义置换。如果选择下一个节点的标准是取最近的一个，则启发式称为最近邻居。这种简单的启发式方法的实际性能较差，许多其他的启发式方法在经验上表现得更好，即建立更便宜的旅行。选择最近的节点是一种公平的直觉，但事实证明远远不能令人满意。有学者建议学习这一选择的标准。他们建立了一个贪婪启发式框架，其中节点选择策略是使用图神经网络来学习的，图神经网络是一种能够通过消息传递机制来处理任意有限大小的输入图的神经网络.对于每个要选择的节点，通过向网络传送问题的图形表示-用指示哪些节点已经被访问的特征来增强-并接收每个节点的动作值。通过强化学习(特别是Q学习)来使用动作值来训练网络，并且部分巡回长度用作奖励。

这个例子对丰富的旅行推销员问题文献没有帮助，这些文献已经开发出比机器学习算法更好的数量级的高级算法。尽管如此，我们在这里要强调的一点是，给定一个固定的上下文，并做出决定，机器学习可以用来发现新的、可能更好的执行策略。即使是最先进的旅行推销员问题算法(即，当精确解达到其极限时)，也以启发式方式做出许多决策，例如切割平面选择，从而为机器学习留出帮助做出这些决策的空间。

我们再次强调，强化学习的马尔可夫决策过程框架很好地描述了通过经验学习策略，其中代理最大化回报（在第 2.2 节中定义）。 通过将奖励信号与优化目标相匹配，学习代理的目标变成了解决问题，而无需假设任何专家知识。 即使优化方法不是强化学习社区的优化方法，也可以在此马尔可夫决策过程公式中转换一些未作为强化学习提出的方法。 例如，部分组合优化文献致力于为不同的问题自动构建专门的启发式算法。 启发式是通过从预定义的特定领域集合中编排一组移动或子例程来构建的。 例如，为了解决bipartite boolean quadratic programming problems，Karapetyan、Punnen 和 Parkes (2017) 将这种编排表示为马尔可夫链，其中状态是子例程(Karapetyan, D., Punnen, A. P., & Parkes, A. J. (2017). Markov chain methods for the bipartite boolean quadratic programming problem. European journal of operational research, 260 (2), 494–506. )。 一条马尔可夫链通过其转移概率进行参数化。 另一方面，有学者通过语法定义了有效的连续动作，其中单词是动作，句子对应于启发式。 作者引入了一个参数空间来表示语法的句子。 在这两种情况下，设置都非常接近强化学习的马尔可夫决策过程，但是通过所谓的自动配置工具（通常基于遗传或局部搜索，以及 利用并行计算）。 请注意，学习设置相当简单，因为参数不适应问题实例，但对于各种集群是固定的。 从机器学习的角度来看，这相当于分段常数回归。 如果要使用更复杂的模型，直接优化可能无法充分扩展以获得良好的性能。 如果不是编排动作集，而是安排预定义的启发式，则可以将构建启发式的相同方法提升一个级别。 由此产生的启发式然后称为超启发式。 有学者通过学习结合现有的启发式方法，为考试时间表构建了一个超启发式方法。 他们使用强盗算法，一种强化学习的无状态形式，在线学习每个启发式的价值函数。

bipartite boolean quadratic programming problems，我们在结束本节时指出，演示和体验并不是相互排斥的，大多数学习任务都可以通过这两种方式来解决。 在混合整数线性规划分支限界树中选择分支变量的情况下，可以采用两种先前策略中的任何一种。 一方面，强分支是一种有效的分支策略，但计算成本太高，并建立了一个机器学习模型来近似它。 另一方面，人们可能认为没有足够好的分支策略并尝试从头开始学习，在传统的变量选择策略中，在分支限界树顶部表现良好的策略不一定与在更深层次表现良好的策略相同。 因此，通过学习一个模型，可以根据树的当前状态在分支定界期间在预定义的策略之间动态切换。 虽然这似乎是一个模仿学习的案例，但鉴于传统的分支策略可以被认为是专家，但实际上并非如此。 实际上，该模型不是向任何专家学习，而是真正学习在现有策略之间进行选择。 这在技术上不是分支变量选择，而是分支启发式选择策略。 每个子树都由一个手工制作的特征向量表示，并对这些向量进行聚类。 与上一段中详细介绍的 Karapetyan 等人的工作类似。 当然，也可以使用自动配置工具为每个集群分配最佳分支策略。 当在给定节点分支时，检索最接近当前子树的集群，并使用其分配的策略。

3.2 算法结构

机器学习独自为问题提供解决方案。在本节中，我们将调查学习到的策略（无论是来自演示还是经验）如何与传统的组合优化算法相结合，也就是说，将机器学习和显式算法视为构建模块，我们调查它们如何在不同的模板中布局。以下三个部分不一定是不相交的，也不一定是详尽的，但它们是审视文献的自然方式。

3.2.1 End to end learning(重要)

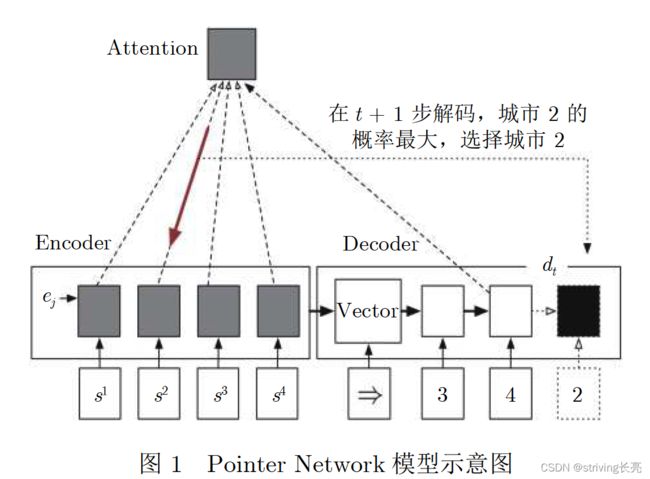
利用机器学习解决离散优化问题的第一个想法是训练机器学习模型直接从输入实例输出解决方案。 最近已经探索了这种方法，特别是在欧几里得旅行商问题上。 为了解决深度学习的问题，引入了指针网络(pointer network)，其中使用编码器，即循环神经网络，解析输入图中的所有旅行商问题节点并生成编码 ( 激活向量）为它们中的每一个。 之后，一个解码器，也是一个循环神经网络，使用类似于 Bahdanau 等人的注意力机制。 在图中先前编码的节点上生成这些节点的概率分布（通过之前图 4 中所示的 softmax 层）。 重复这个解码步骤，网络有可能在其输入（旅行商问题节点）上输出一个排列。 这种方法可以在不同的输入图大小上使用网络。 作者通过以预先计算的旅行商问题解决方案为目标的监督学习来训练模型。 后来有学者使用类似的模型，并使用旅行长度作为奖励信号通过强化学习对其进行训练。 它们**解决了监督（模仿）学习的一些限制，例如需要计算最佳（或至少是高质量）旅行商问题解决方案（目标）**，而当这些解决方案没有精确计算时，这些解决方案可能是不明确的 ，或者当存在多个解决方案时。 后来，有人 在模型中引入了更多的先验知识，使用图神经网络而不是循环神经网络来处理输入。 再后来，有学者通过直接逼近神经网络输出中的双随机矩阵来表征排列，探索了一种不同的方法。 值得注意的是，通过机器学习解决旅行商问题并不新鲜。 九十年代早期的工作集中在 Hopfield 神经网络和自组织神经网络。

在另一个例子中，有学者训练神经网络来预测随机负载规划问题的解决方案，该问题存在确定性混合整数线性规划公式。他们的主要动机是应用程序需要在策略层面做出决策，即在信息不完整的情况下，机器学习用于解决由于缺少观察到的输入中的一些状态变量而引起的问题的随机性。作者使用可操作的解决方案，即问题的确定性版本的解决方案，并将它们聚合为机器学习模型提供（策略上的）解决方案目标。正如他们在论文中所解释的那样，对解决方案的最高描述级别是其成本，而最低（可操作）是对其所有变量的值的了解。然后，作者将自己置于中间，并预测与其特定问题的随机版本相对应的变量聚合（策略上的）。此外，应用程序的性质要求实时输出解决方案，这在使用最先进的混合整数线性规划求解器时，对于随机版本的负荷规划问题或其确定性变量都是不可能的。然后，机器学习被证明适合在较短的计算时间内获得准确的解决方案，因为一些复杂性是离线解决的，即在学习阶段，并且运行时（推理）阶段非常快。最后，请注意在多层感知器，即前馈神经网络，用于将输入实例处理为向量，因此集成了关于问题结构的非常少的先验知识。

3.2.2 Learning to configure algorithms

在许多情况下，仅使用机器学习来解决问题可能不是最合适的方法。相反，可以应用机器学习来为组合优化算法提供附加信息，如图所示,机器学习模型用于使用有价值的信息来增强运筹学算法。

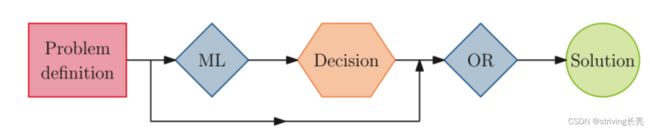
例如，机器学习可以提供算法的参数化（在非常广泛的意义上）。 复杂的优化算法通常有一组在优化过程中保持不变的参数（在机器学习中它们被称为超参数）。例如，这可以是混合整数线性规划求解器的预求解操作（通常由单个参数控制）的激进性，或者是梯度下降方法中的学习率/步长。仔细选择它们的值可以极大地改变优化算法的性能。因此，算法配置社区开始寻找好的默认参数。然后为类似问题实例的不同集群提供良好的默认参数。 从机器学习的角度来看，前者是常数回归，而后者是分段常数最近邻回归。 自然的延续是学习回归映射问题实例到算法参数。

在这种情况下，Kruber、Lübbecke 和 Parmentier (2017) 在混合整数线性规划实例上使用机器学习来预先估计应用 Dantzig-Wolf 分解是否有效，即是否会使求解时间更快。 分解方法可能很强大，但决定是否以及如何应用它们取决于实例及其公式的许多成分，并且没有明确的最佳方式做出这样的决定。 在他们的工作中，数据点被表示为一个固定长度的向量，其特征表示实例和试探性分解统计。 在另一个示例中，在混合整数二次规划的背景下，Bonami、Lodi 和 Zarpellon (2018) 使用机器学习来确定线性化问题是否会更快地解决。 当松弛给出的二次规划问题是凸的，即二次目标矩阵是半正定的，可以通过求解二次规划松弛(注意，凸二次规划可以在多项式时间内求解。) 以提供下界的分支限界算法来解决该问题。 即使在这种凸情况下，也不清楚二次规划分支限界是否比线性化问题（通过使用 McCormick (1976) 不等式）和求解等效混合整数线性规划更快。 这就是为什么机器学习是填补知识空白的绝佳候选者。 在两篇论文（Bonami 等人，2018 年；Kruber 等人，2017 年）中，作者都​​尝试了不同的机器学习模型，例如支持向量机和随机森林，这是在模型中没有嵌入先验知识时的良好实践 . Karapetyan 等人使用的启发式构建框架。 实际上，它可以看作是一个大参数启发式算法，在前一种情况下由转移概率配置，在后一种情况下由表示句子的参数配置。

如前所述，机器学习提供的组合优化算法的参数化要从非常广泛的意义上来理解。 例如，在癌症治疗的放射疗法中，Mahmood、Babier、McNiven、Diamant 和 Chan (2018) 使用机器学习来生成候选疗法，然后通过组合优化算法将其细化为可交付的计划。 即，使用生成对抗网络将 CT 扫描图像着色成潜在的辐射计划，然后对结果应用逆优化 (Ahuja & Orlin, 2001) 以使计划可行 (Chan, Craig, Lee, & Sharpe, 2014 年）。 一般来说，生成对抗网络由两个不同的网络组成：一个（生成器）生成图像，另一个（鉴别器）区分生成的图像和真实图像的数据集。 两者都是交替训练的：判别器通过一个通常的监督目标，而生成器被训练来欺骗判别器。 在Mahmood等人。 （2018），一种特定类型的生成对抗网络（条件生成对抗网络）用于提供着色而不是随机图像。 感兴趣的读者可以参考 Creswell 等人。 （2018）对生成对抗网络的概述。

最后，我们注意到**用于学习某些表示的机器学习模型可以反过来用作由另一个组合优化算法给出的特征段信息**，例如 Kruber 等人使用的分解统计。 (2017) 或 Bonami 等人中的线性规划信息。 （2018 年）。 此外，我们注意到，在可满足性上下文中，学习在特定实例集群上执行的算法类型与学习算法本身的参数是配对的，例如，参见 , Ansótegui, Heymann, Pon, Sellmann, and Tierney (2019)； Ansótegui、Pon、Sellmann 和 Tierney（2017 年）。

3.2.3 Machine learning alongside optimization algorithms

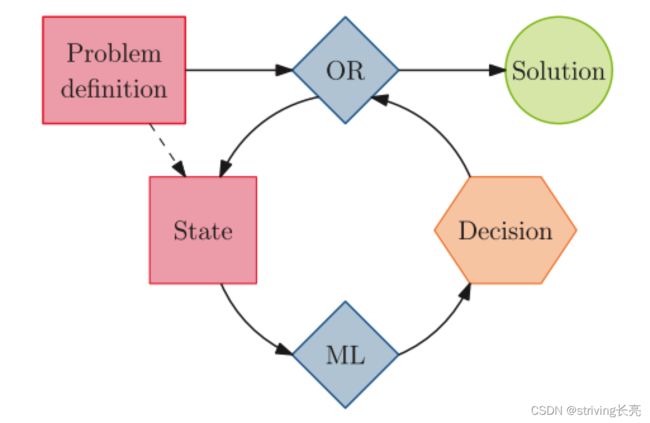
组合优化算法重复查询相同的机器学习模型以做出决策。 机器学习模型将算法的当前状态作为输入，其中可能包括问题定义。

为了将上一节的上下文推广到其全部能力，可以构建组合优化算法，在整个执行过程中重复调用机器学习模型，如上图所示。 主算法控制高级结构，同时经常调用机器学习模型来协助较低级别的决策。 这种方法与上一节中讨论的示例之间的主要区别在于，组合优化算法使用相同的机器学习模型按照算法迭代次数的顺序多次做出相同类型的决策 . 与上一节一样，没有什么能阻止人们在这种算法之前或之后应用额外的步骤。 这显然是混合整数线性规划的分支限界树的上下文，我们已经提到选择分支变量的任务要么太启发式要么太慢，因此是一个很好的学习候选者（Lodi & Zarpellon，2017 年）。 在这种情况下，通用算法仍然是一个分支定界框架，具有相同的软件架构和相同的上下界保证，但每个节点做出的分支决策有待学习。 同样，Hotung 等人的工作。 （2017）学习用于启发式树搜索的分支策略和价值网络无疑适合这种情况。 解决混合整数线性规划的另一个重要方面是使用原始启发式算法，即应用于分支定界节点以找到可行解决方案的算法，但不能保证成功。 除了明显的优势之外，好的解决方案还为解决方案值提供了更严格的上限（用于最小化问题），并使对树的更多修剪成为可能。 启发式取决于分支节点（因为分支将某些变量固定为特定值），因此它们需要经常运行。 然而，过于频繁地运行它们会减慢对树的探索，特别是如果它们的结果是否定的，即没有检测到更好的上限。 Khalil、Dilkina、Nemhauser、Ahmed 和 Shao (2017b) 构建了一个机器学习模型来预测运行给定的启发式算法是否会产生比目前发现的最好的解决方案更好的解决方案，然后在每次测试的结果为正出现时贪婪地运行该启发式算法。

Baltean-Lugojan 等人使用的近似值 (2018)是预测优化问题解决方案的高级描述的示例，即目标值。尽管如此，目标是解决原始的二次规划。因此，学习模型被反复查询以选择有希望的切割平面。机器学习模型仅用于选择有希望的切割，但一旦选择，切割就会被添加到线性规划松弛中，从而将机器学习结果嵌入到精确的算法中。这种方法突出了这种算法的有希望的方向。学到的决定至关重要，因为添加最佳切割平面对于快速解决问题是必要的（或者足够快，因为在存在 NP 难题的情况下，优化可能会在任何有意义的解决之前超时）。同时，近似决策（通常以概率的形式）不会影响算法的准确性：任何添加的切割都保证是有效的。这种设置为机器学习的蓬勃发展留下了空间，同时减少了对机器学习算法（一个活跃且困难的研究领域）的保证需求。此外，请注意，Larsen 等人的方法（2018）是主算法的一部分，其中机器学习被迭代调用以实时做出预订决策。实际上，机器学习模型被要求选择最相关的节点，而主算法则维护部分行程，计算其长度等。因为主算法非常简单，所以可以将贡献视为端到端方法，但也可以更一般地解释为此处所做的。在第 3.1.2 节中介绍并在上一节中提到，用于构建启发式算法的马尔可夫链框架来自 Karapetyan 等人（2017）也可以被视为重复的决定。可以查询和采样转换矩阵，以便从一种状态转换到另一种状态，即做出选择下一步行动的低级决策。

本节中的三个算法结构区别非常笼统，可以重叠。在这里，模型在内部状态转换上运行，但在全局范围内学习，这一事实使其难以分析。值得一提的是，深度学习社区也使用学习循环算法决策，例如，在元学习领域，决定如何在随机梯度下降中应用梯度更新。

4 学习目标(Learning objective)

在上一节中，我们通过将机器学习对组合优化的主要贡献正交分组到方法家族中，对现有文献进行了综述，有时会有重叠。在本节中，我们将制定并研究推动学习过程的目标。

4.1 Multi-instance formulation

下面，我们将介绍一个抽象的学习公式（灵感来源于Bischl等人（2016））。机器学习从业者如何比较优化算法？让我们将I定义为一组问题实例，P是I上的概率分布。这些是我们关心的问题，通过概率分布进行加权，反映出在实际应用中，并非所有问题都有可能发生。在实践中，I或P是不可访问的，但我们可以从P中观察到一些样本，正如蒙特利尔快递公司介绍的那样。对于一组算法a，设$m:I\times A\to R$是算法在问题实例上的性能度量（越低越好）。这可能是找到的最佳解决方案的目标值，但也可能包含来自最优性界限、无结果、运行时间和资源使用的元素。比较$a_1,a_2\in A$， 机器学习实践者会比较$E_{I\sim p}m(i,a_1)$和$E_{I\sim p}m(i,a_2)$，或等效(4)
$$\underset{a\in \left\{a_1,a_2\right\}}{\min }{\mathbb{E}}_{i\sim p}m(i,a)$$
因为测量这些量是不容易处理的，所以通常会使用经验估计来代替，通过使用从 $P$ 中采样的独立实例的有限数据集 $D_{train}$ 序列(5)
$$\underset{a\in \left\{a_1,a_2\right\}}{\min }\sum _{i\in D_{\text{train }}}\frac{1}{\left|D_{\text{train }}\right|}m(i,a)$$
这是直观的并且在实践中完成：收集问题实例的数据集并比较平均运行时间。 当然，可以针对不同的数据集（不同的$I$ 和 $P$）和不同的度量（不同的$ m$）计算这种期望。

这已经是一个学习问题了。 我们想通过学习解决的更一般的问题是(6)
$$\underset{a\in \mathcal{A}}{\min }{\mathbb{E}}_{i\sim P}m(i,a)$$
我们可以在不可数的、可能是非参数的算法空间之间进行比较，而不是在两种算法之间进行比较，并将我们学习的机器学习模型空间视为定义算法空间 $A$ 的参数化。 例如，考虑为分支定界学习分支策略$\pi$ 的情况。 如果我们将策略定义为具有一组权重 $\theta \in {\mathbb{R}}^p$ 的神经网络，那么我们将获得参数分支定界算法 $a({\pi }_{\theta })$ 并且将上式(6)变为(7)
$$\underset{\theta \in {\mathbb{R}}^p}{\min }{\mathbb{E}}_{i\sim P}m\left(i,a\left({\pi }_{\theta }\right)\right)$$
不幸的是，解决这个问题很难。 一方面，性能度量 $m$ 通常是不可微的并且没有封闭形式的表达。 另一方面，计算上式(6)中的期望是棘手的，与(5)一样，可以使用有限数据集使用经验分布，但这会导致泛化考虑。

在继续之前，让我们引入一个新元素以使 公式(6)更通用。 该公式表明，一旦给定一个实例，性能度量的结果就是确定性的。 由于多种原因，这是不现实的。 由于外部因素，性能测量本身可能包含一些随机性来源，例如与硬件和系统相关的运行时间。 该算法还可以包含不可忽略的随机性来源，如果它被设计为随机的，或者如果某些操作是非确定性的，或者表达算法应该对某些外部参数的选择具有鲁棒性的事实。 令$\tau$ 是随机性的来源， $\pi \in \Pi$为正在学习的内部策略，$a(\pi ,\tau )$是结果算法，那么我们可以将(6) 重新表述为(8)
$$\underset{\pi \in \Pi }{\min }{\mathbb{E}}_{i\sim P}\left[{\mathbb{E}}_{\tau }[m(i,a(\pi ,\tau ))\mid i]\right]$$
特别是，当学习重复决策时，如前文所述，这种随机性来源可以沿马尔可夫决策过程中遵循的轨迹表示，使用环境$p\left(s^{\prime },r\mid a,s\right)$的动态。上式(8)中的补充将有助于接下来关于泛化的讨论。

4.2 Surrogate objectives

在上一节中，我们制定了适当的学习目标。 在这里，我们试图将这个目标与学习方法，即演示和经验联系起来。如果机器学习模型的常用学习指标，例如 ，监督（模仿）学习中分类的准确性正在提高，这是否意味着上述公式(6)的性能指标也在提高？

如第 3.1.2 节所述，解决 上述公式(8)的直接方法是强化学习（包括直接优化方法）。 通过将总回报与绩效衡量相匹配，可以直接根据经验数据优化(6)的目标。 有时，单个最终奖励可以自然地在轨迹上解耦。 例如，如果分支定界变量选择策略的性能目标是最小化打开节点的数量，那么该策略可以获得不鼓励节点数量增加的奖励，从而激励选择的变量导致修剪。 然而，这可能并不总是可能的，只剩下将单个奖励延迟到轨迹结束的选项。 这种稀疏的奖励设置对强化学习算法具有挑战性，人们可能想要设计一个替代奖励信号来鼓励中间成就。 这引入了一些差异，并且正在优化的策略可能会学习算法设计者不希望的行为。 两个奖励信号之间没有先验关系。 人们需要利用他们的直觉来设计代理信号，例如 ，最小化分支定界节点的数量应该会导致更小的运行时间。 奖励塑造是强化学习研究的一个活跃领域，但它通常由许多工程技巧来执行。 在从专家演示的监督信号中学习策略的情况下，性能度量 $m$ 甚至不会出现在解决的学习问题中。 在这种情况下，目标是优化动作空间中的策略 $\pi \in \Pi$ 以模仿专家策略 ${\pi }_e$(9)
$$\underset{\pi \in \Pi }{\min }{\mathbb{E}}_{i\sim P}\left[{\mathbb{E}}_s\left[\ell \left(\pi (s),{\pi }_e(s)\right)\mid i,{\pi }_e\right]\right]$$
其中$\ell$是任务相关损失（分类、回归等）。 我们已经强调，状态 $S$ 是有条件的，不仅取决于实例，还取决于用于收集数据的专家策略 ${\pi }_e$。 直观地说，机器学习模型学习得越好，即策略对专家的模仿越好，学习到的策略的最终性能应该越接近专家的性能。 在某些情况下，可以将学习策略的性能与专家策略的性能联系起来，但涵盖这方面的内容超出了本文的范围。 反之则不然，如果学习(模仿)失败，该策略可能仍然表现良好（通过遇到替代的好决策）。 事实上，当做出具有高替代客观误差的决策时，学习将受到完全惩罚，而事实上，该决策在原始指标上可能具有良好的性能。 出于这个原因，体现表现的指标是首要的。 例如， Bonami 等人 (2018) 训练分类器来预测混合整数二次问题实例是否应该线性化。 通过解决两种配置中的问题实例来优化计算用于学习器的目标。 仅仅体现分类准确度是不够的。 实际上，该指标没有提供有关错误分类对运行时间（用于计算目标的指标）影响的信息。 在二元分类中，正确分类的示例也可能恰好在两种配置的运行时间之间具有不显着的差异。 为了缓解这个问题，作者还引入了一个运行时间没有显着差异的类别（并报告了实际运行时间）。 连续扩展将是学习求解时间的回归。 然而，现在学习这种回归意味着最终算法需要对一组决策进行优化以找到最佳决策。 在强化学习中，这类似于学习价值函数。用完全强化学习理论更好地理解对重复决策的相同推理。

4.3 On generalization

在 4.1 节中，我们声称(6)中的概率分布是不可访问的，需要用有限数据集 $D_{train}$ 上的经验概率分布代替，所解决的优化问题是：(10)。
$$\underset{a\in \mathcal{A}}{\min }\sum _{i\in D_{\text{train }}}\frac{1}{\left|D_{\text{train }}\right|}m(i,a)$$
正如第2.2节(Machine Learning)所指出的，当优化经验概率分布时，无论真实概率分布如何，我们都有可能在有限个问题实例上具有低性能度量。在这种情况下，由于训练性能与真实期望性能之间的差异(过拟合)，泛化误差较高。为了控制这一方面，引入验证集$D_{valid}$来比较基于泛化性能估计的有限数量的候选算法，并且使用测试集$D_{test}$来估计所选算法的泛化性能。

在下文中，我们更直观地研究用于组合优化的机器学习中的泛化及其后果。 为了更容易，让我们回顾一下不同的学习场景。 在介绍中，我们提出了蒙特利尔快递公司的例子，其中感兴趣的问题来自蒙特利尔旅行商问题的未知概率分布。 这是一组非常有限的问题，但足以为这项业务创造价值。 更雄心勃勃的是，我们可能希望我们在有限实例集上学习的策略能够在任何“真实世界”混合整数线性规划实例中表现良好（泛化）。 如果您从事销售混合整数线性规划求解器并希望分支策略为尽可能多的客户执行良好的业务，这将很有趣。 在这两种情况下，泛化适用于算法实现者不知道的实例。 这些是我们关心的唯一实例； 用于训练的那个已经解决了。 实例概率分布的主题也自然地出现在随机规划/优化中，其中问题的不确定性通过概率分布建模。 场景生成是解决此类优化程序的基本方法，需要从该分布中采样并多次解决相关问题。 Nair、Dvijotham、Dunning 和 Vinyals（2018 年）利用这一重复过程来学习端到端模型来解决问题。 他们的模型由局部搜索和局部改进策略组成，并通过强化学习进行训练。 在这里，泛化意味着在场景生成期间，学习到的搜索优于其他方法，因此提供了一个整体更快的随机编程算法。 总之，没有泛化的学习是没有意义的！

当策略推广到其他问题实例时，如果训练需要额外的计算来解决问题实例就不再是问题，因为学习可以与解决问题解耦，因为它可以离线完成。 这个设置很有希望，因为它可以为类似的实例提供开箱即用的策略，同时保持学习问题得到预先处理，同时保持合理。 当学习的模型是一个简单的映射时，如第 3.2.2 节（Learning to configure algorithms）中的情况，如前所述，泛化到新实例很容易理解。 然而，在学习顺序决策时，如第 3.2.3 节(Machine learning alongside optimization algorithms)所述，存在复杂的泛化级别。 我们说过我们希望策略泛化到新实例，但是策略也需要泛化到单个实例的算法的内部状态，即使模型可以从完整的优化轨迹中学习，如 (8) 所示。 事实上，复杂的算法可能有意想不到的随机性来源，即使它们被设计为确定性的。 例如，如果某些基础数值库的版本发生更改或由于异步计算（例如使用图形处理单元时），数值近似可能会有所不同（Nagarajan, Warnell, & Stone, 2019）。 此外，即使我们可以实现完美的可复制性，如果求解器的其他一些参数设置（稍微）不同，我们也不希望分支策略中断。 至少，我们希望策略对许多算法中存在的随机种子的选择具有鲁棒性，包括混合整数线性规划求解器。 因此，这些参数可以建模为随机变量。 由于这些嵌套的泛化级别，考虑来自多个实例的训练数据的一种吸引人的方式就像多任务学习设置的单独任务一样。 不同的任务具有共同的潜在方面，并且它们也可能有自己独特的怪癖。 学习在实例分布中泛化的单一策略的一种方法是利用这些共性。 强化学习中的泛化仍然是一个具有挑战性的话题，可能是因为多任务设置和包含所有任务的大型环境之间的模糊区别。

选择一个人在定义分布特征时应该有多大的雄心是一个难题。 例如，如果蒙特利尔公司将业务扩展到其他城市，应该将它们视为单独的分布，并且每个城市学习一个分支政策，还是只学习一个？ 也许每个大陆一个？ 泛化到更多种类的实例具有挑战性，并且需要更高级和更昂贵的学习算法。 为与同一任务相关的不同分布学习一系列机器学习模型当然意味着要训练、维护和部署更多模型。 传统的组合优化算法也是如此，混合整数线性规划求解器本身并不是解决旅行商问题的最佳算法，但它适用于所有混合整数线性规划问题。 鉴于该领域的文献有限，现在就所考虑的分布应该有多广泛提供见解还为时过早。 对于生成合成分布的学者来说，两个直观的研究轴是“结构”和“大小”。 旅行商问题和调度问题的结构似乎完全不同，可以认为两个平面欧几里得旅行商问题更相似。 尽管如此，这些旅行商问题中的两个可能具有显着不同的大小（节点数）。 例如，Gasse 等人。 （2019）在三个分布上独立评估他们的方法。 每个训练数据集都有一个特定的问题结构（集合覆盖、组合拍卖和容量化设施位置）和固定的问题大小。 使用的问题实例生成器是最先进的并且代表真实世界的实例。 尽管如此，当他们评估他们学习的算法时，作者将测试分布推到更大的尺寸。 这背后的想法是衡量学习的模型是否能够泛化到更大、更实用的分布，或者仅在相同大小问题的受限分布上表现良好。 答案在很大程度上是积极的。

4.4 Single instance learning

我们还没有过多讨论的边缘案例是单实例学习框架。 例如，规划单个工厂的设计可能就是这种情况。 工厂只会建造一次，要求非常特殊，规划者没有兴趣将其与其他问题联系起来。 在这种情况下，人们可以根据需要进行尽可能多的运行（episodes）和对潜在专家或模拟器的尽可能多的调用，但最终人们只关心解决这一实例。 学习单个实例的策略应该需要更简单的机器学习模型，因此可能需要更少的训练示例。 尽管如此，在单个实例的情况下，人们在每个新实例中从头开始学习策略，实际上将学习（不是学习模型，而是学习过程本身）结合到最终算法中。 这意味着在学习开始时启动计时器并与其他求解器竞争以最快地获得解决方案（或在时间限制内获得最佳结果）。 这是一个边缘场景，只能在第 3.2.3 节的设置中使用，其中机器学习嵌入在组合优化算法中； 否则将只有一个训练示例！ 因此没有泛化到其他问题实例的概念，因此（6）不是正在解决的学习问题。 尽管如此，该模型仍然需要泛化到算法的未知状态。 实际上，如果模型是从解决问题所需的算法的所有状态中学习的，那么问题在训练时就已经解决了，因此学习是没有结果的。 这是 Khalil 等人遵循的方法。 (2016) ，在第 3.1.1 节中介绍，用于学习特定于实例的分支策略。 该策略是从分支定界树顶部的强分支中学习的，但需要泛化到使用它的树底部的算法状态。 然而，对于所有组合优化算法，与另一种算法的公平比较只能在独立的实例数据集上进行，如 (4) 所示。 这是因为通过人工试验和错误，构建算法时使用的数据会泄漏到算法的设计中，即使没有明确的学习组件。

4.5 Fine tuning and meta-learning

特定于实例的学习和学习通用策略之间的折衷是我们在多任务学习中通常拥有的：一些参数在任务之间共享，而一些参数特定于每个任务。一种**常见的方法（在迁移学习场景中）是从通用策略开始，然后通过一种微调过程将其适应特定实例**：训练分两个阶段进行：

1. 首先在多个阶段训练通用策略来自相同分布的实例，
2. 然后继续对与给定实例相关的示例进行训练，我们希望在这些实例上获得更专业和更准确的预测。

元学习（Meta-Learing），又称“学会学习“（Learning to learn）, 即利用以往的知识经验来指导新任务的学习，使网络具备学会学习的能力，**元学习希望使得模型获取一种学会学习调参的能力，使其可以在获取已有知识的基础上快速学习新的任务。机器学习是先人为调参，之后直接训练特定任务下深度模型。元学习则是先通过其它的任务训练出一个较好的超参数，然后再对特定任务进行训练。**是解决小样本问题（Few-shot Learning）常用的方法之一。

1. 元学习中的”元“是什么意思？
   元学习的本质是增加学习器在多任务的泛化能力，元学习对于任务和数据都需要采样，因此学习到的$F(x)$可以在未出现的任务中迅速（依赖很少的样本）建立起mapping。因此”元“体现在网络对于每个任务的学习，通过不断的适应每个具体任务，使网络具备了一种抽象的学习能力。
2. 元学习中的训练和测试？
   Meta-learning中为了区别概念，将训练过程定义为”Meta-training“、测试过程定义为”Meta-testing“, 如下图所示：
3. ”元学习“和”迁移学习“的区别和联系？
   从目标上看，元学习和迁移学习的本质都是增加学习器在多任务的范化能力，但元学习更偏重于任务和数据的双重采样，即任务和数据一样是需要采样的，具体来说对于一个10分类任务，元学习通过可能只会建立起一个5分类器，每个训练的episode都可以看成是一个子任务，而学习到的$F(x)$可以帮助在未见过的任务里迅速建立mapping。而**迁移学习更多是指从一个任务到其它任务的能力迁移，不太强调任务空间的概念。**

元学习的具体介绍：

• http://news.sohu.com/a/501983069_121119001
• https://blog.csdn.net/langb2014/article/details/84953307
• https://www.zhihu.com/question/299020462
• https://zhuanlan.zhihu.com/p/289043310

元学习和迁移学习领域的机器学习进展在这里特别值得考虑。元学习考虑两个级别的优化：

1. 内循环以依赖元参数的方式在训练集上训练模型的参数，
2. 元参数本身在外循环中进行优化（即，为每个完成的内循环获取梯度培训或更新）。

当外循环的目标函数是验证集上的性能时，我们最终会训练一个系统，以便它能够很好地泛化。如果我们可以访问许多这样的训练任务，这可能是一个成功的策略，可以从很少的例子中进行概括。它与迁移学习有关，我们希望在一个或多个任务中学到的东西有助于提高对另一个任务的泛化能力。这些方法可以帮助快速适应新问题，这在解决许多混合整数线性规划实例（被视为许多相关任务）的上下文中非常有用。

继续使用混合整数线性规划的分支示例，人们可能不希望策略在新实例（来自给定分布）上开箱即用地执行良好。 取而代之的是，人们可能想学习一种策略离线，每次给定一个训练步骤时，它就可以在几个训练步骤中适应新实例。 在自动配置工具的背景下已经探索了类似的主题。 Fitzgerald、Malitsky、O’Sullivan 和 Tierney (2014) 研究了终身学习环境中的自动配置（顺序迁移学习的一种形式）。 自动配置算法增加了一组先前的配置，这些配置优先于任何新的问题实例。 每个配置都保留了反映过去表现的分数。 它旨在保留过去表现良好的配置，同时让新配置有机会得到正确评估。 Lindauer 和 Hutter (2018) 使用的自动配置优化算法需要训练一个经验成本模型，将参数配置和问题实例的笛卡尔积映射到预期的算法性能。 通常为每个需要配置的问题实例集群学习这样的模型。 相反，当呈现一个新的集群时，作者将先前学习的成本模型和新的成本模型结合起来构建一个集成模型。 正如 Fitzgerald 等人所做的那样。 (2014)，作者还构建了一组先前的配置来确定优先级，使用经验成本模型来填充缺失的数据。 此设置比不执行任何策略调整更通用，具有更好的泛化潜力。 再一次，应用的规模可能因雄心而异。 人们可以在非常相似的实例上进行转移，或者学习一种可以转移到大量实例的策略。 元学习算法于 1990 年代首次引入（Bengio, Bengio, Cloutier, & Gecsei, 1991; Schmidhuber, 1992; Thrun & Pratt, 1998），此后在机器学习中变得特别流行，包括但不限于： 学习梯度更新规则 (Andrychowicz et al., 2016; Hochreiter, Younger, & Conwell, 2001)，少镜头学习 (Ravi & Larochelle, 2017) 和多任务强化学习 (Finn, Abbeel, & Levine, 2017) .

4.6 Other metrics

来自学习过程本身的其他度量也是相关的，例如学习过程有多快、样本复杂性（正确拟合模型所需的示例数量）等。与本节前面建议的度量相反，这些度量提供给我们的信息不是关于最终性能，而是关于获得所需策略所需的计算或训练示例数量。当然，这些信息有助于校准将机器学习整合到组合优化算法中的努力。

5 方法论

在上一节中，我们详细阐述了在组合优化算法中使用机器学习的理论学习框架。在这里，我们提供一些额外的讨论，扩大一些先前提出的主张。

5.1 Demonstration and experience

为了学习策略，我们强调了两种方法：

1. 演示，其中预期的行为由专家或预言机展示（有时需要相当大的计算成本）；
   在演示设置中，学习策略的性能受到专家的限制，当专家不是最优时，这是一个限制。更准确地说，在没有奖励信号的情况下，模仿策略只能希望略微优于专家（例如，因为学习者可以减少表现相似的专家之间答案的方差）。学习效果越好，学习者的表现越接近专家的表现。这意味着只有在计算策略的速度明显快于专家时，才应仅使用模仿。此外，学习策略的性能可能无法很好地推广到看不见的示例和任务的小变化，并且可能由于错误的累积而不稳定。这是因为在 (9) 中，数据是根据专家策略 πe 收集的，但是当运行多个重复决策时，状态的分布变成了学习策略的分布。监督（模仿）学习的一些缺点可以通过更先进的算法来克服，包括主动方法来查询专家作为预言机来改善不确定状态下的行为。与机器学习的当前文献相比，这里介绍的模仿学习部分是有限的。
2. 经验，通过反复试验和奖励来学习策略信号。
   相反，通过奖励，算法会学习针对该信号进行优化，并有可能超越任何专家，但代价是更长的训练时间。当多个决策（几乎）与支持一个（任意）决策的专家相比，从奖励信号（经验）中学习也更加灵活。经验并非没有缺陷。在策略是近似的情况下（例如，使用神经网络），如果探索不充分或发现不能很好地概括的解决方案，学习过程可能会陷入糟糕的解决方案。此外，定义奖励信号可能并不总是那么简单。例如，可以使用奖励塑造或课程来增加稀疏奖励，以评估中间成就（参见第 2.2 节）。通常，从专家的演示开始学习，然后使用经验和奖励信号改进策略是一个好主意。这就是最初的 AlphaGo 论文（Silver 等人，2016 年）中所做的，其中将人类知识与强化学习相结合。读者可参考 Hussein、Gaber、Elyan 和 Jayne (2017) 进行的关于模仿学习的调查，该调查涵盖了本节中的大部分讨论。

5.2 Partial observability

我们在第2.2节中提到，有时马尔可夫决策过程的状态没有被完全观察到，马尔可夫属性不成立，即，以当前观察和行动为条件的下一次观察的概率不等于下一次观察的概率以所有过去的观察和行动为条件。 在任何模拟物理的环境中都可以找到一个直接的例子：这种环境的单帧/图像不足以掌握诸如速度之类的概念，因此不足以正确估计物体的未来轨迹。 事实证明，在实际应用中，部分可观察性比异常更接近规范，要么是因为无法访问环境的真实状态，要么是因为它在计算上难以表示并且需要近似 . 解决该问题的一种直接方法是使用循环神经网络压缩所有先前的观察结果。 这可以应用于模仿学习环境以及强化学习，例如通过学习循环策略（Wierstra, Förster, Peters, & Schmidhuber, 2010）。

这在我们想要学习为组合优化算法做出决策的策略函数的情况下如何应用？ 一方面，人们可以完全访问算法的状态，因为它以精确的数学概念表示，例如约束、割、解、分支定界树等。 另一方面，这些状态可以是指数级的。 这是计算和泛化方面的问题。 事实上，如果一个人确实想快速解决问题，那么就需要一个计算速度也很快的策略，尤其是在它被频繁调用的情况下，比如分支决策。 此外，考虑太高维状态也是学习的统计问题，因为它可能会显着增加所需的样本数量、降低学习速度或完全失败。 因此，在尝试数据的不同表示时，有必要牢记这些方面。

5.3 Exactness and approximation

在我们调查的不同例子中，机器学习被用于精确和启发式框架，例如Baltean Lugojan等人（2018年）和Larsen等人（2018年）。让机器学习模型的输出尊从其高级类型约束是一项艰巨的任务。为了用机器学习组件构建精确的算法，有必要在所有可能的决策都有效的情况下应用机器学习。仅使用第3.2.1节中所述的机器学习不能提供任何优化保证，只能提供较弱的可行性保证（见第6.1节）。然而，如果机器学习区分的所有可能选择都导致完整的算法，那么应用机器学习来选择或参数化第3.2.2节中的组合优化算法将保持精确性。最后，在第3.2.3节调查的机器学习和组合优化之间的重复交互情况下，所有可能的决策都必须有效。例如，在混合整数线性规划的情况下，这包括线性规划松弛的分数变量之间的分支，在开放分支节点中选择要探索的节点（He等人，2014），决定在分支和绑定节点上运行启发式的频率（Khalil等人，2017b），在有效不等式中选择切割平面（Baltean-Lugojan等人，2018），删除之前的切割平面（如果它们不是原始约束或分支决策），等等。第3.1.1节中介绍的Hottung等人（2017）的工作中可以找到一个反例。在他们的分支定界框架中，定界是由一个近似的机器学习模型执行的，该模型可能高估下限，从而导致无效的修剪。因此，生成的算法不是一个精确的算法。

6 挑战

在本节中，我们将从相关挑战的角度回顾之前介绍的一些算法概念。

6.1 Feasibility

在第 3.2.1 节中，我们指出了如何使用机器学习直接输出优化问题的解决方案。 与其学习解决方案，不如说该算法正在学习启发式算法。 正如已经反复提到的，学习算法在最优性方面没有给出任何保证，但更关键的是，可行性也没有得到保证。 事实上，我们不知道启发式的输出与最优解的距离有多远，或者它是否尊重问题的约束。 这可能是每个启发式的情况，并且可以通过在精确的优化算法（例如分支定界）中使用启发式来缓解问题。 找到可行的解决方案并不是一个简单的问题（理论上对于混合整数线性规划来说是 NP-hard），但在机器学习中更具挑战性，尤其是通过使用神经网络。 事实上，通过梯度下降训练，必须仔细设计神经架构，以免破坏可微性。 例如，指针网络 (Vinyals et al., 2015) 和 Sinkhorn 层 (Emami & Ranka, 2018) 都是复杂的架构，用于使网络输出排列，这是在编写经典组合优化启发式时容易满足的约束。

6.2 Modelling

一般来说，在机器学习中，特别是在深度学习中，对于某些给定的问题，我们知道一些好的先验知识。 例如，我们知道卷积神经网络是一种在图像数据上比其他网络更容易学习和泛化的架构。 组合优化中研究的问题与机器学习中目前正在解决的问题不同，其中大多数成功的应用程序都针对自然信号。 用于在组合优化中学习良好策略的架构可能与当前用于深度学习的架构大不相同。 这也可能以更微妙或意想不到的方式成为现实：可以想象，反过来，当深度学习应用于组合优化上下文时，深度学习算法的优化组件（例如，对随机梯度下降的修改）可能会有所不同。 当前的深度学习已经提供了许多技术和架构来解决组合优化中感兴趣的问题。 正如第 2.2 节所指出的，参数共享等技术使神经网络可以使用循环神经网络处理可变长度的序列，或者最近通过图神经网络处理图结构化数据。 处理图数据在组合优化中至关重要，因为许多问题都是在图上制定（表示）的。 举一个非常普遍的例子，Selsam 等人（2018）使用关于变量和子句的二分图表示可满足性问题。 这可以推广到混合整数线性规划，其中约束矩阵可以表示为变量和约束的二部图的邻接矩阵，如 Gasse 等人（2019）所做的那样。

6.3 Scaling

扩展到更大的问题可能是一个挑战。如果在某个规模的实例上训练的模型，例如最大 50 个节点的旅行商问题，在更大的实例上进行评估，例如规模为 100、500 个节点等的旅行商问题，则存在泛化方面的挑战，如第 4.3 节所述。事实上，所有通过机器学习解决旅行商问题并试图解决更大实例的论文都认为，随着规模的增加远远超过训练期间看到的规模，性能会下降（Bello et al., 2017; Khalil et al., 2017a; Kool & Welling ，2018 年；Vinyals 等人，2015 年）。为了解决这个问题，人们可能会尝试在更大的实例上学习，但这可能会变成一个计算和泛化问题。除了非常简单的机器学习模型和对数据分布的强假设之外，不可能知道计算复杂度和样本复杂度，即学习所需的观察次数，因为人们不知道自己试图解决的确切问题，即真实数据生成分布。

6.4 Data generation

收集数据（例如优化问题的实例）是一项微妙的任务。 拉森等人 (2018) 声称“在尝试模仿此类数据中反映的行为时，从历史数据中采样是合适的”。 换句话说，给定一个我们观察优化问题实例的外部过程，我们可以收集数据来训练优化所需的一些策略，并期望该策略能够推广到该应用程序的未来实例。 一个实际的例子是经常遇到与其活动相关的优化问题的企业，例如介绍中使用的蒙特利尔快递公司示例。 在其他情况下，即**当我们不针对我们将拥有历史数据的特定应用程序时，我们如何主动训练针对我们还不知道的问题的策略？ 正如第 4.3 节中部分讨论的那样，我们首先需要定义我们想要泛化到哪个实例族**。 例如，我们可能决定学习欧几里得旅行商问题的切割平面选择策略。 即便如此，产生捕捉实际应用本质的问题仍然是一项复杂的工作。 此外，组合优化问题是高维、高度结构化且难以可视化的。 生成图形的唯一训练已经很复杂了！ 尽管如此，这个话题还是引起了一些兴趣。 Smith-Miles 和 Bowly (2015) 声称我们对算法的信心“取决于我们选择测试实例的仔细程度”，但请注意，一种新算法经常被声称“通过证明它优于以前在一组经过充分研究的实例上的方法”。 作者提出了一种问题实例生成方法，包括：定义实例特征空间，在二维中对其进行可视化（使用主成分分析等降维技术），以及使用进化算法将实例生成推向预定义 子空间。 作者认为，如果简单实例和困难实例可以在减少的实例空间中轻松分离，则该方法是成功的。 然后，该方法有效地应用于基于图的问题，但需要重新定义进化原语才能应用于其他类型的问题。 相反，Malitsky、Merschformann、O’Sullivan 和 Tierney (2016) 提出了一种从相同概率分布生成问题实例的方法，在这种情况下，是“工业”布尔可满足性问题实例。 作者使用大型邻域搜索，使用破坏和修复原语来搜索新实例。 计算一些实例特征来分类新实例是否与目标实例属于同一集群。

决定如何表示数据也不是一件容易的事，但会对学习产生巨大的影响。 例如，如何正确地表示一个分支定界节点，甚至是整个分支定界树？ 这些表示需要足够表达以进行学习，但同时又要足够简洁，可以在不进行过多计算的情况下频繁使用。

---

7 总结

本文调查并强调了如何使用机器学习来构建部分学习的组合优化算法。 本文建议，如果学习的策略的计算速度明显快于专家提供的原始策略（在这种情况下是组合优化算法），那么仅模仿学习就很有价值。 相反，如果有足够的训练和有监督的初始化，用奖励信号训练的模型有可能超越当前的策略。 训练一个推广到看不见的问题的策略是一个挑战，这就是为什么我们认为学习应该发生在一个足够小的分布上，这样策略可以充分利用问题的结构并给出更好的结果。 我们相信，通过将机器学习与当前的组合优化算法结合使用，可以改进用于组合优化的端到端机器学习方法，从而受益于现有的理论保证和最先进的算法。

除了绩效激励之外，人们还对使用机器学习作为离散优化的建模工具感兴趣，尽管我们在本文中讨论的大多数方法仍处于探索性部署水平，至少就它们在通用（商业）求解器中的使用而言，我们坚信这只是组合算法新时代的开始 优化算法。