Pytorch 基于经典模型LeNet-5训练MNIST数据集手写数字

LeNet-5简介

LeNet-5官网链接
卷积神经网络是一种特殊的多层神经网络。与几乎所有其他神经网络一样，它们使用反向传播算法版本进行训练。它们的不同之处在于架构。
卷积神经网络旨在通过最少的预处理直接从像素图像中识别视觉模式。
他们可以识别具有极大可变性的模式（例如手写字符），并且对扭曲和简单的几何变换具有鲁棒性。
LeNet-5专为手写和机器打印的字符识别而设计。

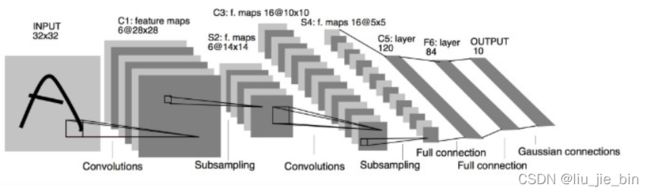
C1层是一个卷积层，有6个卷积核（提取6种局部特征），核大小为5 * 5
S2层是pooling层，下采样（区域:2 * 2 ）降低网络训练参数及模型的过拟合程度。
C3层是第二个卷积层，使用16个卷积核，核大小:5 * 5 提取特征
S4层也是一个pooling层，区域:2*2
C5层是最后一个卷积层，卷积核大小:5 * 5 卷积核种类:120
最后使用全连接层，将C5的120个特征进行分类，最后输出0-9的概率

LeNet-5之所以强大就是因为在当时的环境下将MNIST数据的识别率提高到了99%。以下用MNIST数据进行测试。

准备数据集

Pytorch里面包含了MNIST的数据集，所以我们这里直接使用即可。直接使用DataLoader来对数据进行读取。
训练数据集

train_loader = torch.utils.data.DataLoader(
        datasets.MNIST('data', train=True, download=True, 
                       transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=BATCH_SIZE, shuffle=True)

测试数据集

test_loader = torch.utils.data.DataLoader(
        datasets.MNIST('data', train=False, transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=BATCH_SIZE, shuffle=True)

定义网络

注意：官方教程定义的网络需要32X32大小的出入图片。因为MNIST数据的图像大小为28X28，在这里不改变图像的大小，改变了第一个线性层输入特征的大小。

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 4 * 4, 120)  # 4*4 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square, you can specify with a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        # x = F.relu(self.conv2(x))

        x = torch.flatten(x, 1) # flatten all dimensions except the batch dimension
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        x = F.log_softmax(x, dim=1) # 计算log(softmax(x))
        return x

训练与测试

这里采用的是cpu训练，有gpu的速度会更快。

#定义超参数
BATCH_SIZE=512 
EPOCHS=20 # 总共训练批次
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu") # 让torch判断是否使用GPU，建议使用GPU环境

#声明一个网络
model = Net()
#采用Adam优化器
optimizer = optim.Adam(model.parameters())


#开始训练
for epoch in range(1, EPOCHS + 1):
    # 训练
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if(batch_idx+1)%30 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

    # 测试
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item() # 将一批的损失相加
            pred = output.max(1, keepdim=True)[1] # 找到概率最大的下标
            correct += pred.eq(target.view_as(pred)).sum().item()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

训练结果
Train Epoch: 1 [14848/60000 (25%)] Loss: 0.796161
Train Epoch: 1 [30208/60000 (50%)] Loss: 0.382039
Train Epoch: 1 [45568/60000 (75%)] Loss: 0.258347

Test set: Average loss: 0.2065, Accuracy: 9400/10000 (94%)

Train Epoch: 2 [14848/60000 (25%)] Loss: 0.203479
Train Epoch: 2 [30208/60000 (50%)] Loss: 0.107671
Train Epoch: 2 [45568/60000 (75%)] Loss: 0.143290

Test set: Average loss: 0.1203, Accuracy: 9635/10000 (96%)

Train Epoch: 3 [14848/60000 (25%)] Loss: 0.130832
Train Epoch: 3 [30208/60000 (50%)] Loss: 0.093064
Train Epoch: 3 [45568/60000 (75%)] Loss: 0.097940

Test set: Average loss: 0.0878, Accuracy: 9731/10000 (97%)

Train Epoch: 4 [14848/60000 (25%)] Loss: 0.079764
Train Epoch: 4 [30208/60000 (50%)] Loss: 0.092091
Train Epoch: 4 [45568/60000 (75%)] Loss: 0.083679

Test set: Average loss: 0.0798, Accuracy: 9744/10000 (97%)

Train Epoch: 5 [14848/60000 (25%)] Loss: 0.081892
Train Epoch: 5 [30208/60000 (50%)] Loss: 0.083289
Train Epoch: 5 [45568/60000 (75%)] Loss: 0.068377

Test set: Average loss: 0.0642, Accuracy: 9789/10000 (98%)

Train Epoch: 6 [14848/60000 (25%)] Loss: 0.066107
Train Epoch: 6 [30208/60000 (50%)] Loss: 0.089498
Train Epoch: 6 [45568/60000 (75%)] Loss: 0.042199

Test set: Average loss: 0.0565, Accuracy: 9812/10000 (98%)

Train Epoch: 7 [14848/60000 (25%)] Loss: 0.043734
Train Epoch: 7 [30208/60000 (50%)] Loss: 0.078332
Train Epoch: 7 [45568/60000 (75%)] Loss: 0.054749

Test set: Average loss: 0.0545, Accuracy: 9827/10000 (98%)

Train Epoch: 8 [14848/60000 (25%)] Loss: 0.039079
Train Epoch: 8 [30208/60000 (50%)] Loss: 0.057117
Train Epoch: 8 [45568/60000 (75%)] Loss: 0.062051

Test set: Average loss: 0.0497, Accuracy: 9841/10000 (98%)

Train Epoch: 9 [14848/60000 (25%)] Loss: 0.087467
Train Epoch: 9 [30208/60000 (50%)] Loss: 0.055735
Train Epoch: 9 [45568/60000 (75%)] Loss: 0.030613

Test set: Average loss: 0.0450, Accuracy: 9853/10000 (99%)

Train Epoch: 10 [14848/60000 (25%)] Loss: 0.053619
Train Epoch: 10 [30208/60000 (50%)] Loss: 0.048457
Train Epoch: 10 [45568/60000 (75%)] Loss: 0.050112

Test set: Average loss: 0.0461, Accuracy: 9851/10000 (99%)

Train Epoch: 11 [14848/60000 (25%)] Loss: 0.026218
Train Epoch: 11 [30208/60000 (50%)] Loss: 0.044744
Train Epoch: 11 [45568/60000 (75%)] Loss: 0.044205

Test set: Average loss: 0.0429, Accuracy: 9860/10000 (99%)

Train Epoch: 12 [14848/60000 (25%)] Loss: 0.038024
Train Epoch: 12 [30208/60000 (50%)] Loss: 0.032498
Train Epoch: 12 [45568/60000 (75%)] Loss: 0.047964

Test set: Average loss: 0.0445, Accuracy: 9848/10000 (98%)

Train Epoch: 13 [14848/60000 (25%)] Loss: 0.027184
Train Epoch: 13 [30208/60000 (50%)] Loss: 0.015675
Train Epoch: 13 [45568/60000 (75%)] Loss: 0.021164

Test set: Average loss: 0.0434, Accuracy: 9858/10000 (99%)

Train Epoch: 14 [14848/60000 (25%)] Loss: 0.010554
Train Epoch: 14 [30208/60000 (50%)] Loss: 0.050443
Train Epoch: 14 [45568/60000 (75%)] Loss: 0.018514

Test set: Average loss: 0.0406, Accuracy: 9868/10000 (99%)

Train Epoch: 15 [14848/60000 (25%)] Loss: 0.019876
Train Epoch: 15 [30208/60000 (50%)] Loss: 0.028926
Train Epoch: 15 [45568/60000 (75%)] Loss: 0.062516

Test set: Average loss: 0.0361, Accuracy: 9882/10000 (99%)

Train Epoch: 16 [14848/60000 (25%)] Loss: 0.009616
Train Epoch: 16 [30208/60000 (50%)] Loss: 0.017137
Train Epoch: 16 [45568/60000 (75%)] Loss: 0.034604

Test set: Average loss: 0.0346, Accuracy: 9881/10000 (99%)

Train Epoch: 17 [14848/60000 (25%)] Loss: 0.014641
Train Epoch: 17 [30208/60000 (50%)] Loss: 0.034391
Train Epoch: 17 [45568/60000 (75%)] Loss: 0.006974

Test set: Average loss: 0.0362, Accuracy: 9873/10000 (99%)

Train Epoch: 18 [14848/60000 (25%)] Loss: 0.014653
Train Epoch: 18 [30208/60000 (50%)] Loss: 0.023054
Train Epoch: 18 [45568/60000 (75%)] Loss: 0.008639

Test set: Average loss: 0.0369, Accuracy: 9880/10000 (99%)

Train Epoch: 19 [14848/60000 (25%)] Loss: 0.026135
Train Epoch: 19 [30208/60000 (50%)] Loss: 0.028519
Train Epoch: 19 [45568/60000 (75%)] Loss: 0.023374

Test set: Average loss: 0.0428, Accuracy: 9867/10000 (99%)

Train Epoch: 20 [14848/60000 (25%)] Loss: 0.012330
Train Epoch: 20 [30208/60000 (50%)] Loss: 0.023574
Train Epoch: 20 [45568/60000 (75%)] Loss: 0.030578

Test set: Average loss: 0.0480, Accuracy: 9852/10000 (99%)

准确率达到99%