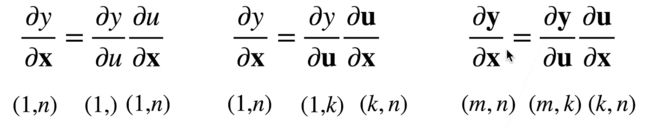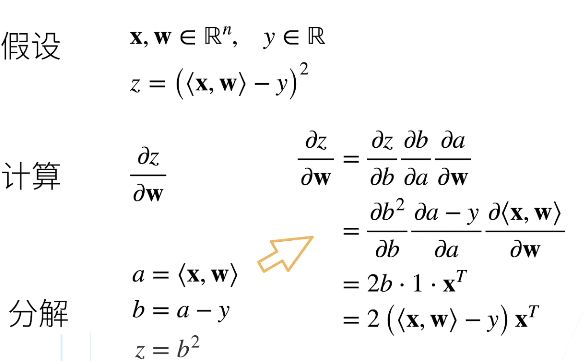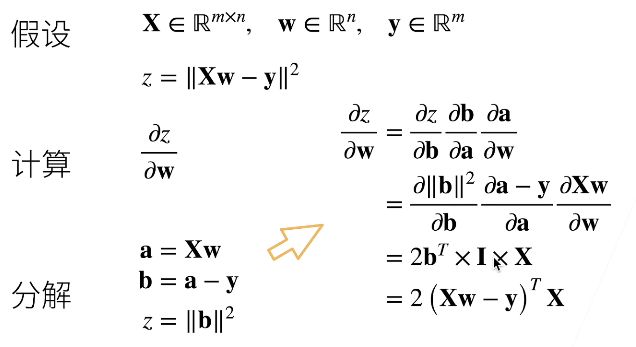深度学习入门之自动求导(Pytorch)
自动求导
-
- 自动求导
-
- 链式法则和自动求导
-
- 向量链式法则
- 例子1
- 例子2
- 自动求导
-
- 计算图
- 自动求导的两种模式
-
- 反向累积
- 反向累积总结
- 复杂度
- 自动求导实现
-
- 自动求导
- QA
自动求导
链式法则和自动求导
向量链式法则
-
标量链式法则
y = f ( u ) , u = g ( x ) ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x y=f(u),u=g(x) \quad\ {\partial y \over \partial x}={\partial y \over \partial u}{\partial u \over \partial x} y=f(u),u=g(x) ∂x∂y=∂u∂y∂x∂u
例子1
例子2
自动求导
- 自动求导计算一个函数在指定值上的导数
- 它有别于
- 符号求导
l n [ 1 ] : = D [ 4 x 3 + x 2 + 3 , x ] ln[1]:= D[4x^3+x^2+3, x] ln[1]:=D[4x3+x2+3,x]
O u t [ 1 ] = 2 x + 12 x 2 Out[1]= 2x+12x^2 Out[1]=2x+12x2 - 数值求导
∂ f ( x ) ∂ x = l i m h − > 0 f ( x + h ) − f ( x ) h {\partial f(x) \over \partial x }= lim_{h->0}{f(x+h) - f(x) \over h} ∂x∂f(x)=limh−>0hf(x+h)−f(x)
- 符号求导
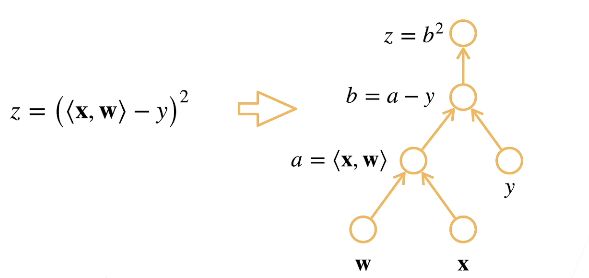
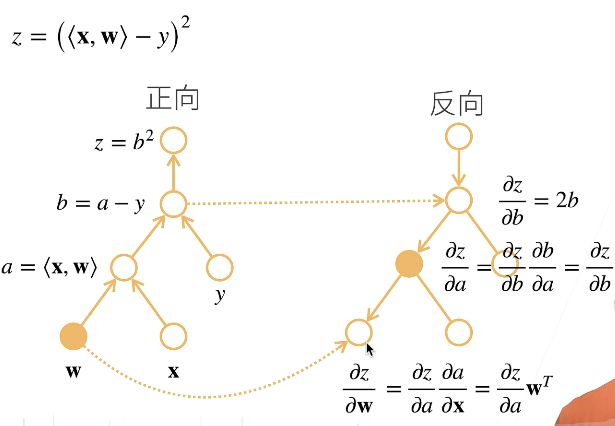
计算图
from mxnet import sym
a = sym.var()
b = sym.var()
c = 2 * a + b
# bind data into a and b later
先定义好公式,再将数值带入
- 隐式构造
- Pytorch/MXNet
from mxnet import autograd, nd
with autograd.record():
a = nd.ones((2, 1))
b = nd.ones((2, 1))
c = 2 * a + b
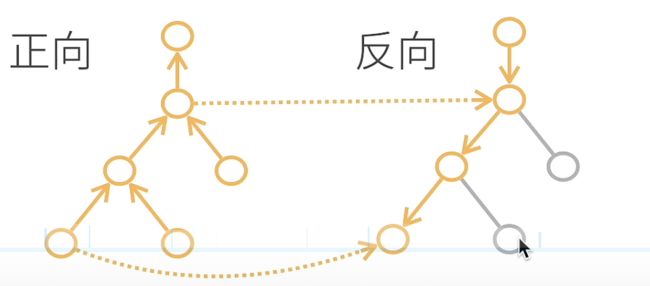
自动求导的两种模式
反向累积
反向累积总结
复杂度
- 计算复杂度:O(n),n是操作子个数
- 通常正向和方向的代价类似
- 内存复杂度:O(n),因为需要存储正向的所有中间结果
因为要存储所有中间结果,所以特别耗GPU资源
- 跟正向累积对比:
- O(n)计算复杂度用来计算一个变量的梯度
- O(1)内存复杂度
自动求导实现
自动求导
假设我们想对函数 y = 2 x T x y = 2x^Tx y=2xTx 关于列向量 x 求导
import torch
x = torch.arange(4.0)
x
tensor([0., 1., 2., 3.])
在我们计算 y 关于 x 的梯度之前,我们需要一个地方来存储梯度。
x.requires_grad(True) # 等价于 `x = torch.arange(4.0, requires_grad=True)`
x.grad # 默认值是None
现在让我们计算y。
y = 2 * torch.dot(x, x)
y
tensor(28.)
通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward()
x.grad
tensor([ 0., 4., 8., 12.])
算出来的值应该是 4x,可以验证一下
x.grad == 4 * x
tensor([True, True, True, True])
现在让我们计算x的另一个函数
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
tensor([1., 1., 1., 1.])
深度学习中,我们的目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
# 对非标量用`backword`需要传入一个`gradient`参数,该参数指定微分参数
x.grad.zero_()
y = x * x
# 等价于y.backword(torch.ones(len(x))
y.sum().backward()
x.grad
tensor([0., 2., 4., 6.])
为什么求导的时候要进行这个sum操作?
梯度只能为标量(即一个数)输出隐式地创建。
将某些计算移动到记录的计算图之外
x.grad.zero_()
y = x * x
u = y.detach() # 将参数常数化
z = u * x
z.sum().backward()
x.grad == u
tensor([True, True, True, True])
后期再将一些网络参数固定住的时候,很有用
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
tensor([True, True, True, True])
即使构建函数的计算图需要通过 Python 控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
a.grad == d / a
tensor(True)
QA
-
显示构造和隐式构造的区别?
显示计算:先给公式再给值
隐式计算:先给值再给公式 -
为什么深度学习一般对标量求导?
因为 Loss 大多时候就是标量。