opencv图像处理学习（二十一）——灰度变换技术

1.Gamma校正

Gamma校正是一种重要的非线性变换，其是对输入图像灰度值进行指数变换，进而校正亮度偏差，通常应用于扩展暗调的细节。一般情况下，当Gamma校正的值大于1时，图像的高光部分被压缩而暗调部分被扩展；当Gamma矫正小于1时，图像的高光部分被扩展而暗调部分被压缩。在最简单的情况下，Gamma矫正通过以下的幂律表达式来定义：,其中A是常数，输入及输出均为非负值，当A=1时，输入与输出的取值范围为0到1，直线变换；当A<1时，低灰度值区域动态范围扩大，进而图像对比度增强，高灰度值区域动态范围缩小，图像对比度降低，图像整体灰度值变大；当A<1时，低灰度值区域的动态范围缩小，进而图像对比度降低，高灰度值区域动态范围扩大，图像对比度增加，图像整体灰度值变小。Gamma校正主要应用在图像增强、目标检测及图像分析等领域。
e.g:

#include 

#include 

#include 

#include 



using namespace cv;

using namespace std;



Mat gammaTramsform(Mat &srcImage,float kFactor)

{

   //建立查表文件LUT

  unsigned char LUT[256];

  for(int i = 0;i<256;i++)

 {

       LUT[i]  =  saturate_cast ( pow( (float) (i/255.0),kFactor) * 255.0f  ;  

 }

Mat resulutImage = srcImage.clone();

if(srcImage.channels() == 1)

{

   MatIterator_ iterator = resultImage.begin();

   MatIterator_  iteratorEnd = resultImage.end();

   for(;iterator ! = iteratorEnd;iterator++)

   {

        *iterator = LUT[(*iterator)];

   }

   else

  {

          MatIterator_ iterator =  resultImage.begin();

          MatIterator_  iteratorEnd = resultImage.end();

  }

for(;iterator ! = iteratorEnd;iterator++)

｛

     (*iterator)[0]  = LUT[(((*iterator)[0] ))];

     (*iterator)[1]  = LUT[(((*iterator)[1] ))];

     (*iterator)[2]  = LUT[(((*iterator)[2] ))];

｝

return resultIamge;

}

int main(void)

{

  Mat srcImage = imread("");//图片路径

  if(!srcImage.data)

  {

     return -1;

  }

 float kFactor1 = 0.3

 float kFactor2 = 3.0;

 Mat result1 = gammaTransform(srcImage,kFactor1);

 Mat result2 = gammaTransform(srcImage,kFactor2);

 imshow("srcImage",srcIamge);

 imshow("result1",result1);

 imshow("result2",result2);

waitkey(0);

return 0;

}

2.线性变换

灰度线性变换是图像处理的基本运算，通常应用在调整图像的画面质量方面，如图像对比度、亮度及反转等操作。对于输入图像f（x，y），输出图像g（x，y），其线性变换其表达式为：g（x,y）=a*f(x,y)+b,其中参数a表示图像对比度变化，b表示图像亮度变化。当a<0时，图像变换代表反转操作，如a=-1、b=255，这是常见的8位灰度图像的反转操作设置参数；当|a|>1时，图像变换代表对比度增加操作；当|a|<1时，图像变换代表对比度减少操作。当b>0时，表示图像变换操作是亮度增加操作；b<0时，表示图像变换操作是亮度减少操作。

e.g:

#include

#include

#include

#include 



using namespace cv;

Mat linearTransform(Mat srcImage,float a,int b)

{

  if(srcImage.empty())

 {

   std::cout<<"No data!"<(i,j)[c] = saturate_cast(a*(srcImage.at(i,j)[c])+b);

  }

 }

}

return resultImage;

}

int main(void)

{

   Mat srcImage = imread("");//图片路径

   if(!srcImage.data)

   {

      returne -1;  

   }

   imshow("srcImage",srcImage);

   waitkey(0);

   float a = 1.2;

   int b = 50;

   Mat new_image = linearTransform(srcImage,a,b);

   imshow("dst",new_image);

   waitKey(0);

   return 0;

}

3.对数变换

图像对数变换是将图像输入中范围较窄的低灰度值映射成输出中较宽范围的灰度值，常用于扩展图像中被压缩的灰度值较高区域的低像素值。对数曲线在像素值比较低的区域斜率大，像素值高的区域斜率比较低，也就是说，图像在较暗的区域对比度得到了提升，因而能增强显示出暗部的细节。对数变换的公式为：s = clog（1+r），其中c为常数，r≥0。图像对数变换的实现可以直接通过对图像中每个元素运算上述公式来完成，也可以通过矩阵整体操作来完成。

PS:convertScaleAbs(Mat Input,Mat Output);

convertScaleAbs()用于实现对整个图像数组中的每一个元素，进行如下操作：

该操作可实现图像增强等相关操作的快速运算，具体用法如下：

e.g:

#include 

#include 

#include 

#include 



using namespace cv;

//对数变换方法1

Mat logTransform1(Mat srcImage,int c)

{

  if(srcImage.empty())

 {

   std::cout<<"No data!"<(i,j);

     gray = c*log((double)(1+gray));

     resultImage.at(i,j)=saturate_cast(gray);

 } 

}

cv::normalize(resultImage,resultImage,0,255,cv::NORM_MINMAX);

cv::convertScaleAbs(resultImage,resultImage);

return resultImage;

}

//对数变换方法3

Mat logTransfom3(Mat srcImage,float c)

{

  if(srcImage.empty())

 {

   std::cout<<"No data!"<

4.对比度拉伸

图像对比度拉伸技术是通过扩展图像灰度级动态范围来实现的，可以扩展对应的全部灰度范围。图像的低对比度一般是由于图像成像亮度不够、成像元器件参数限制或设置不当造成的。提高图像的对比度可以增强图像各个区域的对比效果，对图像中感兴趣的区域进行增强，而对图像中不感兴趣的区域进行相应抑制。常见的三段式分段线性变换函数的公式如下：

分段的灰度拉伸技术可同时结合直方图处理技术，更加灵活地控制输出图像的直方图分布，对特定感兴趣的区域进行对比度调整，增强图像画质。对于集中在较暗的区域，可以采用斜率k>0来进行灰度拉伸扩展，对于图像中较亮的区域，可以采用斜率k<0来进行灰度拉伸压缩。

e.g:

#include core

#include 

#include 

#include 

Mat contrastStretch(Mat srcImage)

{

  Mat resultImage = srcImage.clone();

  int nRows =  resultImage.rows;

  int nCols = resultImage.Cols;

  if(resultImage.isContinuous())

 {

   nCols = nCols * nRows ; 

   nRows =1;

 }

uchar*  pDataMat；

int pixMax = 0 , pixMin = 255;

for(int j = 0;j < nRows; j++)

{

   pDataMat = resultImage.ptr(j);

  for(int i =0;i pixMax)

   {

      pixMax = pDataMat[i];

   }

   if(pDataMat[i] < pixMin)

  {

   pixMin = pDataMat[i];

  }  

 }

return resultImage;

}#include core

#include 

#include 

#include 

Mat contrastStretch(Mat srcImage)

{

  Mat resultImage = srcImage.clone();

  int nRows =  resultImage.rows;

  int nCols = resultImage.Cols;

  if(resultImage.isContinuous())

 {

   nCols = nCols * nRows ; 

   nRows =1;

 }

uchar*  pDataMat；

int pixMax = 0 , pixMin = 255;

for(int j = 0;j < nRows; j++)

{

   pDataMat = resultImage.ptr(j);

  for(int i =0;i pixMax)

   {

      pixMax = pDataMat[i];

   }

   if(pDataMat[i] < pixMin)

  {

   pixMin = pDataMat[i];

  }  

 }

return resultImage;

}

5.灰度级分层

灰度级分层理论是为了更好地提取图像某些区域灰度的亮度特征，常应用于修复某些场景下造成的质量缺陷。（1）将待提取的感兴趣区域的灰度值映射为同一值（最大值），其他不感兴趣的灰度值映射成另一值（最小值），最终输出图像为二值图像。（2）将待提取的感兴趣区域的灰度值映射变大或变小，其他不感兴趣的灰度值保持原有值不变，最终输出图像仍为灰度图像。

6.灰度比特平面

图像像素点是由比特平面构成的，比特平面分层可以更好地描述各个比特平面对图像外观的贡献。在8位灰度图像中，可看作8个1比特的平面构成，其中有4个高阶平面和4个低阶平面，图像高阶数据层主要是视觉感知层及轮廓的相关数据，图像低阶数据层主要是对图像细节部分进行刻画。将一副图像分解为比特平面，对于分析图像中每个比特的相对重要性是十分有用的，该技术常用于数据压缩领域。比特平面编码是一种通过单独处理图像位平面来减少像素间冗余的技术，可将一幅多位图像分解成一系列二值图像并进行相应地编码。一副n比特位图像的灰度级可以用下面的多项式来表示：其中，是平面层的系数，大小取决于该位平面每个像素的取值。

7.最大熵阈值分割

对于图像f(x,y),其分辨率为WxH，灰度级为L，图像中x、y点nxn的邻域平均平均灰度值为：

其中纵坐标必须为证书，即[n/2]是n/2取整，邻域大小通常取3x3，以点灰度及nxn邻域平均灰度建立映射图像F（x,y），用二维阈值｛s，t｝分割图像F（x，y）。令为点灰度与区域灰度均值在（i，j）点发生的概率，根据直方图的定义可以得到的点灰度与区域灰度均值的二维直方图：,图像中边缘及噪声的存在，给提取目标带来了难度，而图像的点灰度与区域灰度均值的二维直方图利用分割阈值矢量，将直方图分成4个区域。根据同态性，目标区域和背景区域所占比例最大，而目标和背景区域内部的像素灰度级比较均匀，像素的灰度值和邻域平均灰度值接近；在目标与背景的分界邻域，像素的灰峰分别对应于目标和背景。因此对分析可知，其会呈现出双峰——谷及极值在对角线附近的特性。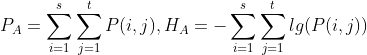设目标区域与背景区域具有不同的概率分布，用目标及背景区域的后验概率对其他区域进行归一化，使目标与背景熵具有可加性，则离散二维熵为：,目标与背景的二维熵的判别函数定义为：,其中,表示（s，t）去最大灰度级时的信息熵，计算方法同。

8.投影峰谷查找

图像的投影特征是分析图像中目标灰度变换规律的重要技术之一，一般通过计算图像的X或Y方向的投影曲线，来分析其波峰波谷分布特征以实现目标分析，该技术常用于图像分割，字符检测及提取及文本分类等领域。对于投影曲线而言，波峰/波谷通常存在于局部最大值点，波谷点是图像的局部最小值点。波峰波谷的计算不能简单通过投影点前后大小比较直接求得，在实际应用中，通常采用差分遍历向量法来实现波峰波谷的查找。

计算步骤如下：（1）计算差分分量（2）判断向量符号（3）遍历差分向量（4）差分遍历判定峰谷