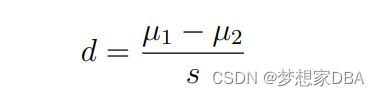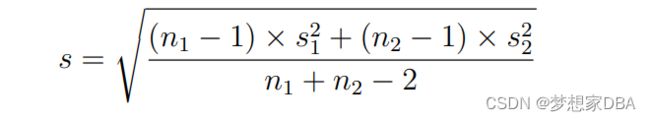About Effect Size
Effect size methods refer to a suite of statistical tools for quantifying the size of an effect in the results of experiments that can be used to complement the results from statistical hypothesis tests.
you will discover effecti size and effect size measures for quantifying the mangnitude of a result.
After completing this tutorial , you will know,
- The importance of calculating and reporting effect size in the results of experiments.
- Effect size measures for quantifying the association between variables, such as Pearson’s correlation coefficient.
- Effect size measures for quantifying the difference between groups, such as Cohen’s d measure.
1.1 Tutorial Overview
- The Need to Report Effect Size
- What Is Effect Size?
- How to Calculate Effect Size
1.2 The Need to Report Effect Size
Once practitioners become versed in statistical methods, it is common to become focused on quantifying the likelihood of a result. This is often seen with the calculation and presentation of the results from statistical hypothesis tests in terms of p-value and the significance level.
The problem with neglecting the presentation of the effect is that it may be calculated using ad hoc measures or even ignored completely and left to the reader to interpret. This is a big problem as quantifying the size of the effect is essential to interpreting results.
1.3 What is Effect Size?
An effect size refers to the size or magnitude of an effect or result as it would be expected to occur in a population. The effect size is estimated from samples of data. Effect size methods refers to a collection of statistical tools used to calculate the effect size. Often the field of effect size measures is referred to as simply effect size, to note the general concern of the field. It is common to organize effect size statistical methods into groups, based on the type of effect that is to be quantified. Two main groups of methods for calculating effect size are:
- Association. Statistical methods for quantifying an association between variables (e.g. correlation).
- Difference. Statistical methods for quantifying the difference between variables (e.g. difference between means).
The result of an effect size calculation must be interpreted, and it depends on the specific statistical method used. A measure must be chosen based on the goals of the interpretation. Three types of calculated result include:
- Standardized Result. The effect size has a standard scale allowing it to be interpreted generally regardless of application (e.g. Cohen’s d calculation).
- Original Units Result. The effect size may use the original units of the variable, which can aid in the interpretation within the domain (e.g. difference between two sample means).
- Unit Free Result. The effect size may not have units such as a count or proportion (e.g. a correlation coefficient).
Thus, effect size can refer to the raw difference between group means, or absolute effect size, as well as standardized measures of effect, which are calculated to transform the effect to an easily understood scale. Absolute effect size is useful when the variables under study have intrinsic meaning (eg, number of hours of sleep).
The effect size does not replace the results of a statistical hypothesis test. Instead, the effect size complements the test. Ideally, the results of both the hypothesis test and the effect size calculation would be presented side-by-side.
- Hypothesis Test: Quantify the likelihood of observing the data given an assumption (null hypothesis).
- Effect Size: Quantify the size of the effect assuming that the effect is present.
1.4 How to Calculate Effect Size
The calculation of an effect size could be the calculation of a mean of a sample or the absolute difference between two means. It could also be a more elaborate statistical calculation. In this section, we will look at some common effect size calculations for both associations and differences. The examples of methods is not complete; there may be 100s of methods that can be used to calculate an effect size.
1.4.1 Calculate Association Effect Size
The association between variables is often referred to as the r family of effect size methods. This name comes from perhaps the most common method for calculating the effect size called Pearson’s correlation coefficient, also called Pearson’s r. The Pearson’s correlation coefficient measures the degree of linear association between two real-valued variables. It is a unit-free effect size measure, that can be interpreted in a standard way, as follows:
- -1.0: Perfect negative relationship.
- -0.7: Strong negative relationship
- -0.5: Moderate negative relationship
- -0.3: Weak negative relationship
- 0.0: No relationship.
- 0.3: Weak positive relationship
- 0.5: Moderate positive relationship
- 0.7: Strong positive relationship
- 1.0: Perfect positive relationship.
The Pearson’s correlation coefficient can be calculated in Python using the pearsonr() SciPy function. Correlation was covered in detail in Chapter 12. The example below demonstrates the calculation of the Pearson’s correlation coefficient to quantify the size of the association between two samples of random Gaussian numbers where one sample has a strong relationship with the second.
# calculate the pearson's correlation between two variables
from numpy.random import randn
from numpy.random import seed
from scipy.stats import pearsonr
# seed random number generator
seed(1)
# prepare data
data1 = 10 * randn(10000) + 50
data2 = data1 + (10 * randn(10000) + 50)
# calculate pearson's correlation
corr,_= pearsonr(data1, data2)
print('Pearsons correlation: %.3f' %corr)Running the example calculates and prints the Pearson’s correlation between the two data samples. We can see that the effect shows a strong positive relationship between the samples.
Pearsons correlation: 0.712
Another very popular method for calculating the association effect size is the r-squared measure, or r 2 , also called the coefficient of determination. It summarizes the proportion of variance in one variable explained by the other.
1.4.2 Calculate Difference Effect Size
The difference between groups is often referred to as the d family of effect size methods. This name comes from perhaps the most common method for calculating the difference between the mean value of groups, called Cohen’s d. Cohen’s d measures the difference between the mean from two Gaussian-distributed variables. It is a standard score that summarizes the difference in terms of the number of standard deviations. Because the score is standardized, there is a table for the interpretation of the result, summarized as:
- Small Effect Size: d=0.20
- Medium Effect Size: d=0.50
- Large Effect Size: d=0.80
The Cohen’s d calculation is not provided in Python; we can calculate it manually. The calculation of the difference between the mean of two samples is as follows:
Where d is the Cohen’s d, µ1 is the mean of the first sample, µ2 is the mean of the second sample, and s is the pooled standard deviation of both samples. The pooled standard deviation for two independent samples can be calculated as follows:
Where s is the pooled standard deviation, n1 and n2 are the size of the first sample and second samples and s 2 1 and s 2 2 is the variance for the first and second samples. The subtractions are the adjustments for the number of degrees of freedom. The function below will calculate the Cohen’s d measure for two samples of real-valued variables. The NumPy functions mean() and var() are used to calculate the sample mean and variance respectively.
# function to calculate Cohen's d for independent samples
def cohend(d1, d2):
# calculate the size of samples
n1, n2 = len(d1), len(d2)
# calculate the variance of the samples
s1, s2 = var(d1, ddof=1), var(d2, ddof=1)
# calculate the pooled standard deviation
s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
# calculate the means of the samples
u1, u2 = mean(d1), mean(d2)
# calculate the effect size
return (u1 - u2) / sThe example below calculates the Cohen’s d measure for two samples of random Gaussian variables with differing means. The example is contrived such that the means are different by one half standard deviation and both samples have the same standard deviation.
# calculate the cohen's d between two sample
from numpy.random import randn
from numpy.random import seed
from numpy import mean
from numpy import var
from math import sqrt
# function to calculate cohen's d for independent samples
def cohend(d1,d2):
# calculate the size of samples
n1, n2 = len(d1),len(d2)
# calculate the variance of the samples
s1, s2 = var(d1, ddof=1), var(d2,ddof=1)
# calculate the pooled standard deviation
s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 -2))
# calculate the means of the samples
u1, u2 = mean(d1), mean(d2)
# calculate the effect size
return (u1 - u2) / s
# seed random number generator
seed(1)
# prepare data
data1 = 10 * randn(10000) + 60
data2 = 10 * randn(10000) + 55
# calculate cohen's d
d = cohend(data1, data2)
print('Cohens d: %.3f' % d)Running the example calculates and prints the Cohen’s d effect size. We can see that as expected, the difference between the means is one half of one standard deviation interpreted as a medium effect size.
Cohens d: 0.500
Two other popular methods for quantifying the difference effect size are:
- Odds Ratio. Measures the odds of an outcome occurring from one treatment compared to another.
- Relative Risk Ratio. Measures the probabilities of an outcome occurring from one treatment compared to another.