一招实时追回逝去的对象——基于当前统计模型(CS模型)的跟踪算法matlab实现
机动目标跟踪——当前统计模型(CS模型)
原创不易,路过的各位大佬请点个赞
针对机动目标跟踪的探讨、技术支持欢迎联系,也可以站内私信
WX: ZB823618313
机动目标跟踪——当前统计模型(CS模型)
- 机动目标跟踪——当前统计模型(CS模型)
-
- 1. 对机动目标跟踪的理解
-
- 1.1. 对机动目标跟踪的理解
- 1.2. 目标模型概述
- 2. "当前"统计CS模型
- 3. "当前"统计CS模型
-
- 3.1. "当前"统计CS模型(连续)
- 3.2. "当前"统计CS模型(离散)
- 3.3. "当前"统计CS模型分析
- 4. "当前"统计CS模型(二维)
-
- 4.1. "当前"统计CS模型(连续)
- 4.2. "当前"统计CS模型(离散)
- 5. 当前统计模型matlab仿真
- 6. 当前统计CS模型三维目标跟踪
- 7. 其它模型
-
- 7.1 匀速转弯CT模型
- 7.2. 匀加速运动CA模型
- 7.3. “当前”统计模型
- 7.4. Singer模型
- 8. 完全代码:联系开头WX
1. 对机动目标跟踪的理解
1.1. 对机动目标跟踪的理解
机动目标跟踪一直是目标跟踪领域研究的难点和重点问题。建立目标运动模型和滤波算法是目标跟踪的两个重要因素。由于目标的机动具有不可预测性,使得我们很难建立精确的目标运动模型。如何建立一种有效的模型来反映目标真实的运动轨迹是高机动目标跟踪系统急需解决的问题。经过近三十年的研究,该领域取得了许多重要成果。
个人理解:机动目标跟踪拥有三要素:
被跟踪目标建模(本博客重点讲:当前统计模型)
传感器测量(另一个博客介绍)
滤波器设计(见目标跟踪专栏)
从算法层面,在目标跟踪系统中,常用的滤波算法是以卡尔曼滤波器为基本框架的估计算法。卡尔曼滤波器是一种线性、无偏、以误差均方差最小为准则的最优估计算法,它有精确的数学形式和优良的使用效能。卡尔曼滤波方法实质上是一种数据处理方法,它采用递推滤波方法,根据获取的量测数据由递推方程递推给出新的状态估计。由于计算量和存储量小,比较容易满足实时计算的要求,在工程实践中得到广泛应用。
除此之外,非线性滤波也广泛应用与机动目标跟踪,比如:
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …
1.2. 目标模型概述
机动目标模型描述了目标状态随着时间变化的过程。一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后,基于状态空间的机动目标建模成为主要研究对象之一。
常用的目标运动模型包括:
匀速运动模型,CV
匀加速运动模型,CA
匀速转弯模型,CT
Singer 模型
“当前”统计模型
Jerk 模型
目标的空间运动基于不同的运动轨迹和坐标系
一维运动
二维运动
三维运动根据不同方向的运动是否相关
坐标间不耦合模型
坐标间耦合模型
2. "当前"统计CS模型
“当前”统计模型是由周宏仁于年提出来的。从本质上讲,该算法模型是一个具有非零均值的加速度的模型。该算法认为当目标正以某一加速度机动时,下一刻的加速度取值是有限的,且只能在“当前”加速度的邻域内。其机动加速度的“当前”统计概率密度采用修正瑞利分布来描述,均值为“当前”加速度的预测值。
Singer 模型所描述的目标的机动建立在两条假设条件之下,即加速度是零均值的
和加速度的概率密度函数是服从均匀分布的。
“当前”统计模型(Current Statistical Model)是针对 Singer 的这两条假设条件提出的修正模型,使其更符合实际的情况,即认为目标在当前时刻以某一加速度机动时,利用机动的当前统计特性可知下一时刻的加速度的取值不是随机的,而是在有限范围内即“当前”加速度的邻域内。
通过这样模型就建立新的两条假设之下,即加速度非零均值且其概率密度服从修正的瑞利分布,实际滤波时用当前时刻的状态估计的预测加速度去代替加速度的均值。
其加速度符合非零均值一阶时间相关马尔科夫过程,即
x ¨ ( t ) = a ˉ ( t ) + a ( t ) a ˙ ( t ) = − α a ( t ) + w ( t ) (1) \ddot{x}(t)=\bar{a}(t) + a(t)\\ \dot{a}(t)=-\alpha a(t) + w(t) \tag{1} x¨(t)=aˉ(t)+a(t)a˙(t)=−αa(t)+w(t)(1)
其中 a ˉ ( t ) \bar{a}(t) aˉ(t) 为加速度均值, a ( t ) a(t) a(t)为零均值的有色噪声, w ( t ) w(t) w(t) 是均值为 0,方差为 2 α σ 2 2\alpha\sigma^2 2ασ2的高斯白噪声。
3. "当前"统计CS模型
3.1. "当前"统计CS模型(连续)
由于“当前”统计模型(Current Statistical Model)是针对 Singer 的这两条假设条件提出的修正模型,
因此 “当前”统计模型的状态方程与 Singer 模型类似,可表示为:
令状态向量为
X = [ x , x ˙ , x ¨ ] T {X}=[x, \dot{x},\ddot{x}]^T X=[x,x˙,x¨]T
则加速度为
a ( t ) = x ¨ ( t ) a(t)=\ddot{x}(t) a(t)=x¨(t)
连续时间Singer模型为
X ˙ ( t ) = [ 0 1 0 0 0 1 0 0 − α ] X ( t ) + [ 0 0 α ] a ˉ ( t ) + [ 0 0 1 ] w ( t ) \dot{X}(t)=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}X(t) + \begin{bmatrix}0\\0\\\alpha\end{bmatrix}\bar{a}(t) + \begin{bmatrix}0\\0\\1\end{bmatrix}w(t) X˙(t)=⎣⎡00010001−α⎦⎤X(t)+⎣⎡00α⎦⎤aˉ(t)+⎣⎡001⎦⎤w(t)
Singer模型也可以表述为
X ˙ ( t ) = A X ( t ) + B u a ˉ ( t ) + B w ( t ) \dot{X}(t)=AX(t) + B_u\bar{a}(t) + Bw(t) X˙(t)=AX(t)+Buaˉ(t)+Bw(t)
其中
A = [ 0 1 0 0 0 1 0 0 − α ] , B u = [ 0 0 α ] , B = [ 0 0 1 ] A=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}, B_u=\begin{bmatrix}0\\0\\\alpha\end{bmatrix}, B= \begin{bmatrix}0\\0\\1\end{bmatrix} A=⎣⎡00010001−α⎦⎤,Bu=⎣⎡00α⎦⎤,B=⎣⎡001⎦⎤
3.2. "当前"统计CS模型(离散)
周期T采样离散化后,转化为离散时间状态方程为:
X k + 1 = F k X k + G k a ˉ k + W k (2) X_{k+1}=F_kX_{k} +G_k\bar{a}_k + W_k \tag{2} Xk+1=FkXk+Gkaˉk+Wk(2)
其中
F k = [ 1 T ( α T − 1 + e − α T ) / α 2 0 1 ( 1 − e − α T ) / α 0 0 − e − α T ] F_k=\begin{bmatrix}1&T&(\alpha T-1+e^{-\alpha T})/\alpha^2\\0&1&(1-e^{-\alpha T})/\alpha\\0&0&-e^{-\alpha T}\end{bmatrix} Fk=⎣⎡100T10(αT−1+e−αT)/α2(1−e−αT)/α−e−αT⎦⎤
G k = [ ( − T + α T 2 2 + 1 − e − α T α ) / α T − ( 1 − e − α T ) / α 1 − e − α T ] G_k=\begin{bmatrix}(-T+\frac{\alpha T^2}{2} + \frac{1-e^{-\alpha T}}{\alpha})/\alpha\\ T - (1-e^{-\alpha T})/\alpha\\ 1-e^{-\alpha T}\end{bmatrix} Gk=⎣⎡(−T+2αT2+α1−e−αT)/αT−(1−e−αT)/α1−e−αT⎦⎤
a ˉ k \bar{a}_k aˉk可用当前时刻的状态估计中的预测加速度来替代:
a ˉ k = x ¨ ^ k ∣ k − 1 \bar{a}_k=\hat{\ddot{x}}_{k|k-1} aˉk=x¨^k∣k−1
噪声 W k W_k Wk的方差为
Q = 2 α σ 2 [ q 11 q 12 q 13 q 21 q 22 q 23 q 31 q 32 q 33 ] Q=2\alpha \sigma^2 \begin{bmatrix}q_{11}&q_{12}&q_{13}\\q_{21}&q_{22}&q_{23}\\q_{31}&q_{32}&q_{33}\end{bmatrix} Q=2ασ2⎣⎡q11q21q31q12q22q32q13q23q33⎦⎤
Q Q Q为对称矩阵
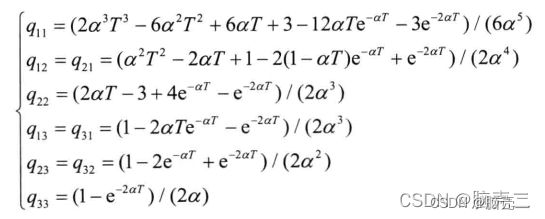
其中但 σ 2 \sigma^2 σ2为:
σ 2 = { 4 − π π [ a m a x − a ˉ k ] 2 , a ˉ k ≥ 0 4 − π π [ a m a x + a ˉ k ] 2 , a ˉ k < 0 (3) \sigma^2= \begin{cases}\frac{4-\pi}{\pi} [a_{max}-\bar{a}_k]^2, \bar{a}_k\geq0 \\ \frac{4-\pi}{\pi} [a_{max}+\bar{a}_k]^2, \bar{a}_k<0\end{cases}\tag{3} σ2={π4−π[amax−aˉk]2,aˉk≥0π4−π[amax+aˉk]2,aˉk<0(3)
对于"当前"统计模型CS,其中矩阵 F k F_k Fk与Singer模型一样
对于"当前"统计模型CS,其中噪声方差 W k W_k Wk均与Singer模型一样,除了 σ 2 \sigma^2 σ2的确定不一样
3.3. "当前"统计CS模型分析
“当前”统计模型利用加速度的预测值来实时地自适应地调整过程参数 σ 2 \sigma^2 σ2 ,有了极强的自适应性。因此,“当前”统计模型比 Singer 模型能反映更真实的目标机动加速度的变化。同时,“当前”统计模型在滤波的每一个时刻都在修正模型的加速度,可以对速度突变的运动的目标进行很好的跟踪。而且就算法而言,“当前”统计模型和 Singer 模型几乎一模一样,唯一的不同只是利用在滤波过程中就求得的当前加速度的预测值改变了运动状态方程。
“当前”加速度在目标机动强烈的情况下,具有比 Singer模型更好的机动描述能力,即基于该模型的相应滤波器具有更好的估计精度。
其具有如下两个特点:
-
当目标无机动时,即理论加速度趋于0时,相应加速度估计值 a ^ k − 1 \hat{a}_{k-1} a^k−1,应趋于0,此时采用式(3)计算的 σ 2 \sigma^2 σ2趋于 ( 4 − π ) a m a x 2 π \frac{(4-\pi)a_{max}^2}{\pi} π(4−π)amax2。该方差是所有可能方差的最大值,表明当目标无机动时,加速度具有最大的变化可能性。这会导致基于该模型的状态估计值在无机动时具有相应较大的方差。
-
当目标机动最大或最小,即理论加速度为 ± a m a x ±a_{max} ±amax时,相应的加速度估计值 a ^ k − 1 \hat{a}_{k-1} a^k−1也应趋于 ± a m a x ±a_{max} ±amax,此时 σ 2 \sigma^2 σ2的计算值趋于0。该方差为所有可能方差的最小值,表明当目标进行最强机动运动时,加速度变化的可能性最小。这与实际中加速度在任何时候均可能有一定变化的现象不符,从而导致相应的估计值在机动加速度绝对值较大且发生突变时具有较大的估计误差。
4. "当前"统计CS模型(二维)
二维的当前统计模型和一维类似,只需要矩阵对角堆叠就可以了
类似的,三维的当前统计模型也类似。
4.1. "当前"统计CS模型(连续)
令状态向量为
X = [ x , x ˙ , x ¨ , y , y ˙ , y ¨ ] T {X}=[x, \dot{x},\ddot{x},y, \dot{y},\ddot{y}]^T X=[x,x˙,x¨,y,y˙,y¨]T
则加速度为
a ( t ) = [ x ¨ ( t ) , y ¨ ( t ) ] T a(t)=[\ddot{x}(t), \ddot{y}(t)]^T a(t)=[x¨(t),y¨(t)]T
加速度均值为:
a ˉ ( t ) = [ a ˉ x ( t ) , a ˉ y ( t ) ] T \bar{a}(t) =[\bar{a}_x(t) , \bar{a}_y(t) ]^T aˉ(t)=[aˉx(t),aˉy(t)]T
连续时间Singer模型为
X ˙ ( t ) = [ 0 1 0 0 0 0 0 0 1 0 0 0 0 0 − α 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 − α ] X ( t ) + [ 0 0 0 0 α 0 0 0 0 0 0 α ] a ˉ ( t ) + [ 0 0 0 0 1 0 0 0 0 0 0 1 ] w ( t ) \dot{X}(t)=\begin{bmatrix}0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&-\alpha&0&0&0 \\0&0&0&0 &1&0\\0&0&0&0 &0&1 \\0&0&0&0 &0&-\alpha \end{bmatrix} X(t) + \begin{bmatrix}0 &0\\0&0\\\alpha&0 \\ 0&0\\0&0\\0&\alpha\end{bmatrix}\bar{a}(t) +\begin{bmatrix}0&0\\0&0\\1&0\\ 0&0\\0&0\\0&1\end{bmatrix}w(t) X˙(t)=⎣⎢⎢⎢⎢⎢⎢⎡00000010000001−α00000000000010000001−α⎦⎥⎥⎥⎥⎥⎥⎤X(t)+⎣⎢⎢⎢⎢⎢⎢⎡00α00000000α⎦⎥⎥⎥⎥⎥⎥⎤aˉ(t)+⎣⎢⎢⎢⎢⎢⎢⎡001000000001⎦⎥⎥⎥⎥⎥⎥⎤w(t)
为了方便,定义
A = [ 0 1 0 0 0 1 0 0 − α ] , B u = [ 0 0 α ] , B = [ 0 0 1 ] A=\begin{bmatrix}0&1&0\\0&0&1\\0&0&-\alpha\end{bmatrix}, B_u=\begin{bmatrix}0\\0\\\alpha\end{bmatrix}, B= \begin{bmatrix}0\\0\\1\end{bmatrix} A=⎣⎡00010001−α⎦⎤,Bu=⎣⎡00α⎦⎤,B=⎣⎡001⎦⎤
则上式变为
X ˙ ( t ) = [ A 0 0 A ] X ( t ) + [ B u 0 0 B u ] a ˉ ( t ) + [ B 0 0 B ] w ( t ) \dot{X}(t)=\begin{bmatrix}A&0\\0&A \end{bmatrix}X(t) + \begin{bmatrix}B_u&0\\0&B_u\end{bmatrix}\bar{a}(t) + \begin{bmatrix}B&0\\0&B\end{bmatrix}w(t) X˙(t)=[A00A]X(t)+[Bu00Bu]aˉ(t)+[B00B]w(t)
4.2. "当前"统计CS模型(离散)
周期T采样离散化后,转化为离散时间状态方程为:
X k + 1 = F k X k + G k a ˉ k + W k X_{k+1}=F_kX_{k} +G_k\bar{a}_k + W_k Xk+1=FkXk+Gkaˉk+Wk
其中
F k = [ F 0 0 F ] F_k=\begin{bmatrix}F&0\\0&F \end{bmatrix} Fk=[F00F]
F = [ 1 T ( α T − 1 + e − α T ) / α 2 0 1 ( 1 − e − α T ) / α 0 0 − e − α T ] F=\begin{bmatrix}1&T&(\alpha T-1+e^{-\alpha T})/\alpha^2\\0&1&(1-e^{-\alpha T})/\alpha\\0&0&-e^{-\alpha T}\end{bmatrix} F=⎣⎡100T10(αT−1+e−αT)/α2(1−e−αT)/α−e−αT⎦⎤
其中
G k = [ G 0 0 G ] G_k=\begin{bmatrix}G&0\\0&G \end{bmatrix} Gk=[G00G]
G = [ ( − T + α T 2 2 + 1 − e − α T α ) / α T − ( 1 − e − α T ) / α 1 − e − α T ] G_=\begin{bmatrix}(-T+\frac{\alpha T^2}{2} + \frac{1-e^{-\alpha T}}{\alpha})/\alpha\\ T - (1-e^{-\alpha T})/\alpha\\ 1-e^{-\alpha T}\end{bmatrix} G=⎣⎡(−T+2αT2+α1−e−αT)/αT−(1−e−αT)/α1−e−αT⎦⎤
噪声 W k W_k Wk的方差为
Q k = [ Q 0 0 Q ] Q_k=\begin{bmatrix}Q&0\\0&Q \end{bmatrix} Qk=[Q00Q]
Q = 2 α σ 2 [ q 11 q 12 q 13 q 21 q 22 q 23 q 31 q 32 q 33 ] Q=2\alpha \sigma^2 \begin{bmatrix}q_{11}&q_{12}&q_{13}\\q_{21}&q_{22}&q_{23}\\q_{31}&q_{32}&q_{33}\end{bmatrix} Q=2ασ2⎣⎡q11q21q31q12q22q32q13q23q33⎦⎤
Q Q Q为对称矩阵,且
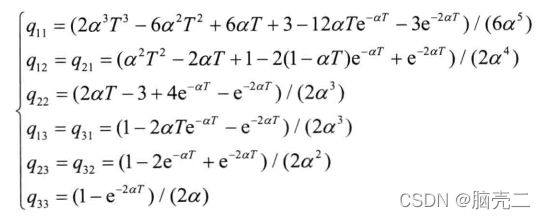
其中但 σ 2 \sigma^2 σ2为:
σ 2 = { 4 − π π [ a m a x − a ˉ k ] 2 , a ˉ k ≥ 0 4 − π π [ a m a x + a ˉ k ] 2 , a ˉ k < 0 (3) \sigma^2= \begin{cases}\frac{4-\pi}{\pi} [a_{max}-\bar{a}_k]^2, \bar{a}_k\geq0 \\ \frac{4-\pi}{\pi} [a_{max}+\bar{a}_k]^2, \bar{a}_k<0\end{cases}\tag{3} σ2={π4−π[amax−aˉk]2,aˉk≥0π4−π[amax+aˉk]2,aˉk<0(3)
如果对于x 和 y 维的噪声方差不一样,则分别计算Q,其它的类似,这里当作相等计算
5. 当前统计模型matlab仿真
位置轨迹: 图1
速度轨迹: 图2
加速度轨迹: 图3
加速度变化率轨迹: 图4
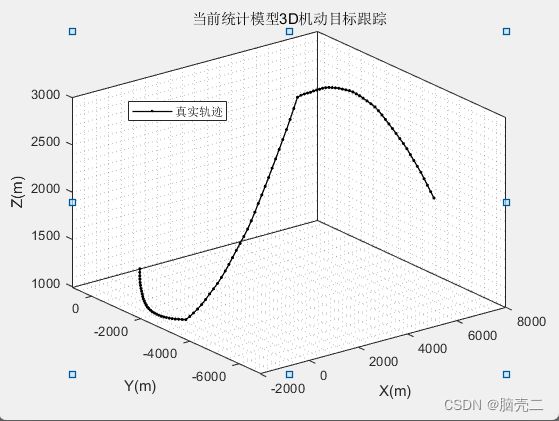
6. 当前统计CS模型三维目标跟踪
算法:卡尔曼滤波
容积卡尔曼滤波
无迹卡尔曼滤波
测量:雷达
跟踪轨迹如下:
7. 其它模型
7.1 匀速转弯CT模型
匀速转弯CT运动模型见另一个博客:包括二维、三维
7.2. 匀加速运动CA模型
匀加速运动CA模型见另一个博客
7.3. “当前”统计模型
当前统计模型见另一个博客
7.4. Singer模型
Singer模型见另一个博客
8. 完全代码:联系开头WX
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%跟踪轨迹
figure
plot3(sV(1,:,1,1),sV(4,:,1,1),sV(7,:,1,1),'.-k',eV(1,:,1,1),eV(4,:,1,1),eV(7,:,1,1),'--r',eV(1,:,1,2),eV(4,:,1,2),eV(7,:,1,2),'-.b','LineWidth',1)
xlabel('X(m)');ylabel('Y(m)');zlabel('Z(m)');
grid minor;
box on;
legend('真实轨迹','无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
title('当前统计模型3D机动目标跟踪')
%%%%%%%%%%各个维度(X Y Z)跟踪轨迹
ii=1:N; % 1 3 5指的是位置,2 4 5 指的是速度
%%%%%%%% X 跟踪轨迹
figure
plot(ii,sV(1,ii,1,1),'.-k',ii,meaV(1,ii,1),'-g',ii,eV(1,ii,1,1),'--r',ii,eV(1,ii,1,2),'-.b','LineWidth',1)
xlabel('时间(s)');
ylabel('m');
legend('真实轨迹','雷达测量','无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
title('跟踪轨迹:X 维')
%%%%%%%% Y 跟踪轨迹
figure
ii=1:N;
plot(ii,sV(4,ii,1,1),'.-K',ii,meaV(2,ii,1),'-g',ii,eV(4,ii,1,1),'--r',ii,eV(4,ii,1,2),'-.b','LineWidth',1)
%plot3(sV(1,:,1,1),sV(3,:,1,1),sV(5,:,1,1),'g',xV(1,:,1,1),xV(3,:,1,1),xV(5,:,1,1),'b')
xlabel('时间(s)');
ylabel('m');
legend('真实轨迹','雷达测量','无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
title('跟踪轨迹:Z 维')
%%%%%%%% Z 跟踪轨迹
figure
ii=1:N;
plot(ii,sV(7,ii,1,1),'.-K',ii,meaV(3,ii,1),'-g',ii,eV(7,ii,1,1),'--r',ii,eV(7,ii,1,2),'-.b','LineWidth',1)
%plot3(sV(1,:,1,1),sV(3,:,1,1),sV(5,:,1,1),'g',xV(1,:,1,1),xV(3,:,1,1),xV(5,:,1,1),'b')
xlabel('时间(s)');
ylabel('m');
legend('真实轨迹','雷达测量','无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
title('跟踪轨迹:Z 维')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% %%%画RMSE
for i=1:MC
sprintf('rate of process:%3.1f%%',(3*MC+i)/(4*MC)*100)
for k=1:N
for c=1:chan
error(:,c)=sV(:,k,i,1)-eV(:,k,i,c);
% RMSE
error2(:,c)=error(:,c).^2;
error2_dis(c)=error2(1,c)+error2(4,c)+error2(7,c);
error2_vel(c)=error2(2,c)+error2(5,c)+error2(8,c);
position(k,i,c)=error2_dis(c);
velocity(k,i,c)=error2_vel(c);
end
end
end
%% RMSE
for c=1:chan
rms_position(:,c)=sqrt(sum(position(:,:,c),2)./MC);
rms_velocity(:,c)=sqrt(sum(velocity(:,:,c),2)./MC);
end
ii=1:N;
figure;%position
plot(ii,rms_position(ii,1),'-*r',ii,rms_position(ii,2),'-cs','LineWidth',1);
% legend('EKF','UF')
legend('无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
xlabel('t/s');ylabel('Position RMSE');
figure;%速度
plot(ii,rms_velocity(ii,1),'-*r',ii,rms_velocity(ii,2),'-cs','LineWidth',1);
legend('无迹卡尔曼滤波 ','容积卡尔曼滤波 ')
xlabel('t/s');ylabel('Velocity RMSE');
==原创不易,路过的各位大佬请点个赞=