时间序列预测——GRU
本文展示了使用GRU进行时间序列预测的全过程,包含详细的注释。整个过程主要包括:数据导入、数据清洗、结构转化、建立GRU模型、训练模型(包括动态调整学习率和earlystopping的设置)、预测、结果展示、误差评估等完整的时间序列预测流程。
本文使用的数据集在本人上传的资源中,链接为mock_kaggle.csv
import pandas as pd
import numpy as np
import math
from matplotlib import pyplot as plt
from matplotlib.pylab import mpl
import tensorflow as tf
from sklearn.preprocessing import MinMaxScaler
from keras import backend as K
from keras.layers import LeakyReLU
from sklearn.metrics import mean_squared_error # 均方误差
from keras.callbacks import LearningRateScheduler
from keras.callbacks import EarlyStopping
from tensorflow.keras import Input, Model,Sequential
mpl.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
mpl.rcParams['axes.unicode_minus']=False #显示负号
取数据
data=pd.read_csv('mock_kaggle.csv',encoding ='gbk',parse_dates=['datetime'])
Date=pd.to_datetime(data.datetime)
data['date'] = Date.map(lambda x: x.strftime('%Y-%m-%d'))
datanew=data.set_index(Date)
series = pd.Series(datanew['股票'].values, index=datanew['date'])
series
date
2014-01-01 4972
2014-01-02 4902
2014-01-03 4843
2014-01-04 4750
2014-01-05 4654
...
2016-07-27 3179
2016-07-28 3071
2016-07-29 4095
2016-07-30 3825
2016-07-31 3642
Length: 937, dtype: int64
滞后扩充数据
dataframe1 = pd.DataFrame()
num_hour = 16
for i in range(num_hour,0,-1):
dataframe1['t-'+str(i)] = series.shift(i)
dataframe1['t'] = series.values
dataframe3=dataframe1.dropna()
dataframe3.index=range(len(dataframe3))
dataframe3
| t-16 | t-15 | t-14 | t-13 | t-12 | t-11 | t-10 | t-9 | t-8 | t-7 | t-6 | t-5 | t-4 | t-3 | t-2 | t-1 | t | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4972.0 | 4902.0 | 4843.0 | 4750.0 | 4654.0 | 4509.0 | 4329.0 | 4104.0 | 4459.0 | 5043.0 | 5239.0 | 5118.0 | 4984.0 | 4904.0 | 4822.0 | 4728.0 | 4464 |
| 1 | 4902.0 | 4843.0 | 4750.0 | 4654.0 | 4509.0 | 4329.0 | 4104.0 | 4459.0 | 5043.0 | 5239.0 | 5118.0 | 4984.0 | 4904.0 | 4822.0 | 4728.0 | 4464.0 | 4265 |
| 2 | 4843.0 | 4750.0 | 4654.0 | 4509.0 | 4329.0 | 4104.0 | 4459.0 | 5043.0 | 5239.0 | 5118.0 | 4984.0 | 4904.0 | 4822.0 | 4728.0 | 4464.0 | 4265.0 | 4161 |
| 3 | 4750.0 | 4654.0 | 4509.0 | 4329.0 | 4104.0 | 4459.0 | 5043.0 | 5239.0 | 5118.0 | 4984.0 | 4904.0 | 4822.0 | 4728.0 | 4464.0 | 4265.0 | 4161.0 | 4091 |
| 4 | 4654.0 | 4509.0 | 4329.0 | 4104.0 | 4459.0 | 5043.0 | 5239.0 | 5118.0 | 4984.0 | 4904.0 | 4822.0 | 4728.0 | 4464.0 | 4265.0 | 4161.0 | 4091.0 | 3964 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 916 | 1939.0 | 1967.0 | 1670.0 | 1532.0 | 1343.0 | 1022.0 | 813.0 | 1420.0 | 1359.0 | 1075.0 | 1015.0 | 917.0 | 1550.0 | 1420.0 | 1358.0 | 2893.0 | 3179 |
| 917 | 1967.0 | 1670.0 | 1532.0 | 1343.0 | 1022.0 | 813.0 | 1420.0 | 1359.0 | 1075.0 | 1015.0 | 917.0 | 1550.0 | 1420.0 | 1358.0 | 2893.0 | 3179.0 | 3071 |
| 918 | 1670.0 | 1532.0 | 1343.0 | 1022.0 | 813.0 | 1420.0 | 1359.0 | 1075.0 | 1015.0 | 917.0 | 1550.0 | 1420.0 | 1358.0 | 2893.0 | 3179.0 | 3071.0 | 4095 |
| 919 | 1532.0 | 1343.0 | 1022.0 | 813.0 | 1420.0 | 1359.0 | 1075.0 | 1015.0 | 917.0 | 1550.0 | 1420.0 | 1358.0 | 2893.0 | 3179.0 | 3071.0 | 4095.0 | 3825 |
| 920 | 1343.0 | 1022.0 | 813.0 | 1420.0 | 1359.0 | 1075.0 | 1015.0 | 917.0 | 1550.0 | 1420.0 | 1358.0 | 2893.0 | 3179.0 | 3071.0 | 4095.0 | 3825.0 | 3642 |
921 rows × 17 columns
二折划分数据并标准化
# pot=int(len(dataframe3)*0.8)
pd.DataFrame(np.random.shuffle(dataframe3.values)) #shuffle
pot=len(dataframe3)-12
train=dataframe3[:pot]
test=dataframe3[pot:]
scaler = MinMaxScaler(feature_range=(0, 1)).fit(train)
#scaler = preprocessing.StandardScaler().fit(train)
train_norm=pd.DataFrame(scaler.fit_transform(train))
test_norm=pd.DataFrame(scaler.transform(test))
test_norm.shape,train_norm.shape
((12, 17), (909, 17))
X_train=train_norm.iloc[:,1:]
X_test=test_norm.iloc[:,1:]
Y_train=train_norm.iloc[:,:1]
Y_test=test_norm.iloc[:,:1]
转换为3维数据 [samples, timesteps, features]
source_x_train=X_train
source_x_test=X_test
X_train=X_train.values.reshape([X_train.shape[0],8,2]) #从(909, 16)-->(909, 8,2)
X_test=X_test.values.reshape([X_test.shape[0],8,2]) #从(12, 16)-->(12, 8,2)
Y_train=Y_train.values
Y_test=Y_test.values
X_train.shape,Y_train.shape
((909, 8, 2), (909, 1))
X_test.shape,Y_test.shape
((12, 8, 2), (12, 1))
动态调整学习率与提前终止函数
def scheduler(epoch):
# 每隔50个epoch,学习率减小为原来的1/10
if epoch % 50 == 0 and epoch != 0:
lr = K.get_value(gru.optimizer.lr)
if lr>1e-5:
K.set_value(gru.optimizer.lr, lr * 0.1)
print("lr changed to {}".format(lr * 0.1))
return K.get_value(gru.optimizer.lr)
reduce_lr = LearningRateScheduler(scheduler)
early_stopping = EarlyStopping(monitor='loss',
patience=20,
min_delta=1e-5,
mode='auto',
restore_best_weights=False,#是否从具有监测数量的最佳值的时期恢复模型权重
verbose=2)
构造GRU模型
# 特征数
input_dim = X_train.shape[2]
# 时间步长:用多少个时间步的数据来预测下一个时刻的值
time_steps = X_train.shape[1]
batch_size = 32
gru = Sequential()
input_layer =Input(batch_shape=(batch_size,time_steps,input_dim))
gru.add(input_layer)
gru.add(tf.keras.layers.GRU(64))
gru.add(tf.keras.layers.Dense(32))
gru.add(tf.keras.layers.LeakyReLU(alpha=0.3))
gru.add(tf.keras.layers.Dense(16))
gru.add(tf.keras.layers.LeakyReLU(alpha=0.3))
gru.add(tf.keras.layers.Dense(1))
gru.add(tf.keras.layers.LeakyReLU(alpha=0.3))
# 定义优化器
nadam = tf.keras.optimizers.Nadam(lr=1e-3)
gru.compile(loss = 'mse',optimizer = nadam,metrics = ['mae'])
gru.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru (GRU) (32, 64) 13056
_________________________________________________________________
dense (Dense) (32, 32) 2080
_________________________________________________________________
leaky_re_lu (LeakyReLU) (32, 32) 0
_________________________________________________________________
dense_1 (Dense) (32, 16) 528
_________________________________________________________________
leaky_re_lu_1 (LeakyReLU) (32, 16) 0
_________________________________________________________________
dense_2 (Dense) (32, 1) 17
_________________________________________________________________
leaky_re_lu_2 (LeakyReLU) (32, 1) 0
=================================================================
Total params: 15,681
Trainable params: 15,681
Non-trainable params: 0
_________________________________________________________________
训练
history=gru.fit(X_train,Y_train,validation_split=0.1,epochs=80,batch_size=32,callbacks=[reduce_lr])
Train on 818 samples, validate on 91 samples
Epoch 1/80
818/818 [==============================] - 7s 9ms/sample - loss: 0.0248 - mae: 0.1090 - val_loss: 0.0531 - val_mae: 0.1838
Epoch 2/80
818/818 [==============================] - 0s 352us/sample - loss: 0.0135 - mae: 0.0831 - val_loss: 0.0456 - val_mae: 0.1769
Epoch 3/80
818/818 [==============================] - 0s 360us/sample - loss: 0.0107 - mae: 0.0744 - val_loss: 0.0352 - val_mae: 0.1586
Epoch 4/80
818/818 [==============================] - 0s 423us/sample - loss: 0.0089 - mae: 0.0661 - val_loss: 0.0312 - val_mae: 0.1527
Epoch 5/80
818/818 [==============================] - 0s 431us/sample - loss: 0.0086 - mae: 0.0630 - val_loss: 0.0259 - val_mae: 0.1328
Epoch 6/80
818/818 [==============================] - 0s 332us/sample - loss: 0.0068 - mae: 0.0561 - val_loss: 0.0265 - val_mae: 0.1202
Epoch 7/80
818/818 [==============================] - 0s 325us/sample - loss: 0.0056 - mae: 0.0514 - val_loss: 0.0219 - val_mae: 0.1227
Epoch 8/80
818/818 [==============================] - 0s 345us/sample - loss: 0.0058 - mae: 0.0524 - val_loss: 0.0203 - val_mae: 0.1073
Epoch 9/80
818/818 [==============================] - 0s 376us/sample - loss: 0.0058 - mae: 0.0508 - val_loss: 0.0234 - val_mae: 0.1070
Epoch 10/80
818/818 [==============================] - 0s 339us/sample - loss: 0.0048 - mae: 0.0467 - val_loss: 0.0192 - val_mae: 0.1073
Epoch 11/80
818/818 [==============================] - 0s 329us/sample - loss: 0.0046 - mae: 0.0456 - val_loss: 0.0174 - val_mae: 0.1115
Epoch 12/80
818/818 [==============================] - 0s 355us/sample - loss: 0.0049 - mae: 0.0457 - val_loss: 0.0203 - val_mae: 0.1009
Epoch 13/80
818/818 [==============================] - 0s 331us/sample - loss: 0.0044 - mae: 0.0441 - val_loss: 0.0169 - val_mae: 0.0912
Epoch 14/80
818/818 [==============================] - 0s 329us/sample - loss: 0.0043 - mae: 0.0427 - val_loss: 0.0174 - val_mae: 0.0909
Epoch 15/80
818/818 [==============================] - 0s 343us/sample - loss: 0.0042 - mae: 0.0435 - val_loss: 0.0145 - val_mae: 0.0940
Epoch 16/80
818/818 [==============================] - 0s 363us/sample - loss: 0.0044 - mae: 0.0424 - val_loss: 0.0184 - val_mae: 0.0915
Epoch 17/80
818/818 [==============================] - 0s 339us/sample - loss: 0.0037 - mae: 0.0392 - val_loss: 0.0137 - val_mae: 0.0787
Epoch 18/80
818/818 [==============================] - 0s 328us/sample - loss: 0.0039 - mae: 0.0395 - val_loss: 0.0134 - val_mae: 0.0974
Epoch 19/80
818/818 [==============================] - 0s 362us/sample - loss: 0.0040 - mae: 0.0417 - val_loss: 0.0122 - val_mae: 0.0784
Epoch 20/80
818/818 [==============================] - 0s 363us/sample - loss: 0.0034 - mae: 0.0375 - val_loss: 0.0155 - val_mae: 0.0823
Epoch 21/80
818/818 [==============================] - 0s 434us/sample - loss: 0.0034 - mae: 0.0369 - val_loss: 0.0152 - val_mae: 0.0836
Epoch 22/80
818/818 [==============================] - 0s 392us/sample - loss: 0.0032 - mae: 0.0358 - val_loss: 0.0309 - val_mae: 0.1415
Epoch 23/80
818/818 [==============================] - 0s 355us/sample - loss: 0.0055 - mae: 0.0444 - val_loss: 0.0123 - val_mae: 0.0828
Epoch 24/80
818/818 [==============================] - 0s 375us/sample - loss: 0.0037 - mae: 0.0407 - val_loss: 0.0124 - val_mae: 0.0752
Epoch 25/80
818/818 [==============================] - 0s 344us/sample - loss: 0.0032 - mae: 0.0364 - val_loss: 0.0133 - val_mae: 0.0686
Epoch 26/80
818/818 [==============================] - 0s 331us/sample - loss: 0.0040 - mae: 0.0403 - val_loss: 0.0126 - val_mae: 0.0735
Epoch 27/80
818/818 [==============================] - 0s 330us/sample - loss: 0.0028 - mae: 0.0331 - val_loss: 0.0110 - val_mae: 0.0667
Epoch 28/80
818/818 [==============================] - 0s 343us/sample - loss: 0.0028 - mae: 0.0321 - val_loss: 0.0108 - val_mae: 0.0605
Epoch 29/80
818/818 [==============================] - 0s 344us/sample - loss: 0.0036 - mae: 0.0371 - val_loss: 0.0115 - val_mae: 0.0675
Epoch 30/80
818/818 [==============================] - 0s 352us/sample - loss: 0.0035 - mae: 0.0394 - val_loss: 0.0147 - val_mae: 0.0685
Epoch 31/80
818/818 [==============================] - 0s 400us/sample - loss: 0.0028 - mae: 0.0319 - val_loss: 0.0118 - val_mae: 0.0668
Epoch 32/80
818/818 [==============================] - 0s 332us/sample - loss: 0.0032 - mae: 0.0347 - val_loss: 0.0118 - val_mae: 0.0659
Epoch 33/80
818/818 [==============================] - 0s 352us/sample - loss: 0.0031 - mae: 0.0355 - val_loss: 0.0130 - val_mae: 0.0689
Epoch 34/80
818/818 [==============================] - 0s 344us/sample - loss: 0.0029 - mae: 0.0330 - val_loss: 0.0104 - val_mae: 0.0700
Epoch 35/80
818/818 [==============================] - 0s 333us/sample - loss: 0.0026 - mae: 0.0305 - val_loss: 0.0133 - val_mae: 0.0660
Epoch 36/80
818/818 [==============================] - 0s 332us/sample - loss: 0.0028 - mae: 0.0327 - val_loss: 0.0107 - val_mae: 0.0604
Epoch 37/80
818/818 [==============================] - 0s 358us/sample - loss: 0.0031 - mae: 0.0342 - val_loss: 0.0121 - val_mae: 0.0608
Epoch 38/80
818/818 [==============================] - 0s 453us/sample - loss: 0.0030 - mae: 0.0329 - val_loss: 0.0100 - val_mae: 0.0702
Epoch 39/80
818/818 [==============================] - 0s 595us/sample - loss: 0.0030 - mae: 0.0321 - val_loss: 0.0112 - val_mae: 0.0720
Epoch 40/80
818/818 [==============================] - 0s 582us/sample - loss: 0.0034 - mae: 0.0359 - val_loss: 0.0104 - val_mae: 0.0688
Epoch 41/80
818/818 [==============================] - 0s 426us/sample - loss: 0.0029 - mae: 0.0317 - val_loss: 0.0109 - val_mae: 0.0691
Epoch 42/80
818/818 [==============================] - 0s 536us/sample - loss: 0.0028 - mae: 0.0311 - val_loss: 0.0108 - val_mae: 0.0632
Epoch 43/80
818/818 [==============================] - 0s 482us/sample - loss: 0.0026 - mae: 0.0302 - val_loss: 0.0102 - val_mae: 0.0668
Epoch 44/80
818/818 [==============================] - 0s 499us/sample - loss: 0.0028 - mae: 0.0323 - val_loss: 0.0106 - val_mae: 0.0569
Epoch 45/80
818/818 [==============================] - 0s 466us/sample - loss: 0.0027 - mae: 0.0308 - val_loss: 0.0119 - val_mae: 0.0662
Epoch 46/80
818/818 [==============================] - 0s 351us/sample - loss: 0.0027 - mae: 0.0329 - val_loss: 0.0113 - val_mae: 0.0777
Epoch 47/80
818/818 [==============================] - 0s 497us/sample - loss: 0.0026 - mae: 0.0303 - val_loss: 0.0110 - val_mae: 0.0631
Epoch 48/80
818/818 [==============================] - 0s 363us/sample - loss: 0.0028 - mae: 0.0315 - val_loss: 0.0113 - val_mae: 0.0696
Epoch 49/80
818/818 [==============================] - 0s 363us/sample - loss: 0.0024 - mae: 0.0287 - val_loss: 0.0108 - val_mae: 0.0680
Epoch 50/80
818/818 [==============================] - 0s 343us/sample - loss: 0.0028 - mae: 0.0313 - val_loss: 0.0100 - val_mae: 0.0600
lr changed to 0.00010000000474974513
Epoch 51/80
818/818 [==============================] - 0s 338us/sample - loss: 0.0022 - mae: 0.0260 - val_loss: 0.0099 - val_mae: 0.0646
Epoch 52/80
818/818 [==============================] - 0s 338us/sample - loss: 0.0022 - mae: 0.0269 - val_loss: 0.0103 - val_mae: 0.0600
Epoch 53/80
818/818 [==============================] - 0s 337us/sample - loss: 0.0022 - mae: 0.0255 - val_loss: 0.0101 - val_mae: 0.0620
Epoch 54/80
818/818 [==============================] - 0s 346us/sample - loss: 0.0021 - mae: 0.0256 - val_loss: 0.0103 - val_mae: 0.0628
Epoch 55/80
818/818 [==============================] - 0s 346us/sample - loss: 0.0021 - mae: 0.0254 - val_loss: 0.0103 - val_mae: 0.0624
Epoch 56/80
818/818 [==============================] - 0s 338us/sample - loss: 0.0021 - mae: 0.0256 - val_loss: 0.0102 - val_mae: 0.0620
Epoch 57/80
818/818 [==============================] - 0s 338us/sample - loss: 0.0021 - mae: 0.0255 - val_loss: 0.0103 - val_mae: 0.0627
Epoch 58/80
818/818 [==============================] - 0s 333us/sample - loss: 0.0021 - mae: 0.0252 - val_loss: 0.0100 - val_mae: 0.0644
Epoch 59/80
818/818 [==============================] - 0s 345us/sample - loss: 0.0021 - mae: 0.0260 - val_loss: 0.0099 - val_mae: 0.0624
Epoch 60/80
818/818 [==============================] - 0s 337us/sample - loss: 0.0021 - mae: 0.0255 - val_loss: 0.0103 - val_mae: 0.0627
Epoch 61/80
818/818 [==============================] - 0s 323us/sample - loss: 0.0021 - mae: 0.0256 - val_loss: 0.0100 - val_mae: 0.0617
Epoch 62/80
818/818 [==============================] - 0s 344us/sample - loss: 0.0021 - mae: 0.0251 - val_loss: 0.0098 - val_mae: 0.0638
Epoch 63/80
818/818 [==============================] - 0s 311us/sample - loss: 0.0021 - mae: 0.0257 - val_loss: 0.0102 - val_mae: 0.0634
Epoch 64/80
818/818 [==============================] - 0s 332us/sample - loss: 0.0021 - mae: 0.0257 - val_loss: 0.0099 - val_mae: 0.0595
Epoch 65/80
818/818 [==============================] - 0s 315us/sample - loss: 0.0021 - mae: 0.0254 - val_loss: 0.0100 - val_mae: 0.0607
Epoch 66/80
818/818 [==============================] - 0s 384us/sample - loss: 0.0021 - mae: 0.0253 - val_loss: 0.0101 - val_mae: 0.0611
Epoch 67/80
818/818 [==============================] - 0s 365us/sample - loss: 0.0021 - mae: 0.0254 - val_loss: 0.0098 - val_mae: 0.0613
Epoch 68/80
818/818 [==============================] - 0s 409us/sample - loss: 0.0021 - mae: 0.0254 - val_loss: 0.0102 - val_mae: 0.0610
Epoch 69/80
818/818 [==============================] - 0s 386us/sample - loss: 0.0021 - mae: 0.0256 - val_loss: 0.0103 - val_mae: 0.0600
Epoch 70/80
818/818 [==============================] - 0s 346us/sample - loss: 0.0021 - mae: 0.0249 - val_loss: 0.0099 - val_mae: 0.0603
Epoch 71/80
818/818 [==============================] - 0s 367us/sample - loss: 0.0021 - mae: 0.0255 - val_loss: 0.0100 - val_mae: 0.0610
Epoch 72/80
818/818 [==============================] - 0s 366us/sample - loss: 0.0021 - mae: 0.0251 - val_loss: 0.0101 - val_mae: 0.0620
Epoch 73/80
818/818 [==============================] - 0s 327us/sample - loss: 0.0021 - mae: 0.0253 - val_loss: 0.0099 - val_mae: 0.0613
Epoch 74/80
818/818 [==============================] - 0s 321us/sample - loss: 0.0021 - mae: 0.0251 - val_loss: 0.0099 - val_mae: 0.0635
Epoch 75/80
818/818 [==============================] - 0s 328us/sample - loss: 0.0021 - mae: 0.0251 - val_loss: 0.0098 - val_mae: 0.0616
Epoch 76/80
818/818 [==============================] - 0s 328us/sample - loss: 0.0021 - mae: 0.0252 - val_loss: 0.0097 - val_mae: 0.0603
Epoch 77/80
818/818 [==============================] - 0s 318us/sample - loss: 0.0021 - mae: 0.0254 - val_loss: 0.0098 - val_mae: 0.0602
Epoch 78/80
818/818 [==============================] - 0s 320us/sample - loss: 0.0021 - mae: 0.0255 - val_loss: 0.0101 - val_mae: 0.0599
Epoch 79/80
818/818 [==============================] - 0s 341us/sample - loss: 0.0021 - mae: 0.0250 - val_loss: 0.0098 - val_mae: 0.0617
Epoch 80/80
818/818 [==============================] - 0s 335us/sample - loss: 0.0021 - mae: 0.0251 - val_loss: 0.0098 - val_mae: 0.0616
history.history.keys() #查看history中存储了哪些参数
plt.plot(history.epoch,history.history.get('loss')) #画出随着epoch增大loss的变化图
预测
predict = gru.predict(X_test)
real_predict=scaler.inverse_transform(np.concatenate((source_x_test,predict),axis=1))
real_y=scaler.inverse_transform(np.concatenate((source_x_test,Y_test),axis=1))
real_predict=real_predict[:,-1]
real_y=real_y[:,-1]
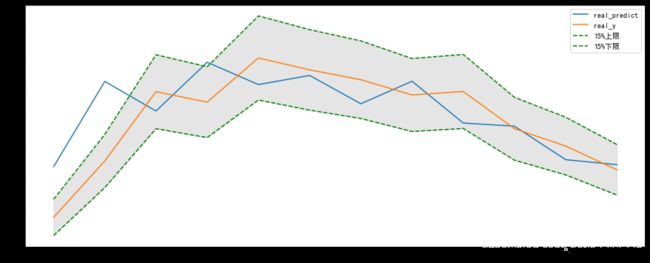
误差评估
plt.figure(figsize=(15,6))
bwith = 0.75 #边框宽度设置为2
ax = plt.gca()#获取边框
ax.spines['bottom'].set_linewidth(bwith)
ax.spines['left'].set_linewidth(bwith)
ax.spines['top'].set_linewidth(bwith)
ax.spines['right'].set_linewidth(bwith)
plt.plot(real_predict,label='real_predict')
plt.plot(real_y,label='real_y')
plt.plot(real_y*(1+0.15),label='15%上限',linestyle='--',color='green')
# plt.plot(real_y*(1+0.1),label='10%上限',linestyle='--')
# plt.plot(real_y*(1-0.1),label='10%下限',linestyle='--')
plt.plot(real_y*(1-0.15),label='15%下限',linestyle='--',color='green')
plt.fill_between(range(0,12),real_y*(1+0.15),real_y*(1-0.15),color='gray',alpha=0.2)
plt.legend()
plt.show()
round(mean_squared_error(Y_test,predict),4)
0.0014
from sklearn.metrics import r2_score
round(r2_score(real_y,real_predict),4)
0.4542
per_real_loss=(real_y-real_predict)/real_y
avg_per_real_loss=sum(abs(per_real_loss))/len(per_real_loss)
print(avg_per_real_loss)
0.13512234237078294
#计算指定置信水平下的预测准确率
#level为小数
def comput_acc(real,predict,level):
num_error=0
for i in range(len(real)):
if abs(real[i]-predict[i])/real[i]>level:
num_error+=1
return 1-num_error/len(real)
comput_acc(real_y,real_predict,0.2),comput_acc(real_y,real_predict,0.15),comput_acc(real_y,real_predict,0.1)
(0.8333333333333334, 0.75, 0.6666666666666667)