西瓜书第六章笔记及答案——支持向量机

第6章 支持向量机

6.1间隔与支持向量

支持向量（support vector）：距离超平面最近的且满足一定条件的几个训练样本点
间隔（margin）：两个不同类别的支持向量到超平面的距离之和

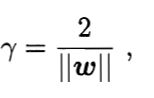
支持向量机（support vector machine）：最大化间隔

6.2对偶问题

对偶问题（dual problem）：实质相同但从不同角度提出不同提法的一对问题。
支持向量机本身是一个凸二次规划问题（convex quadratic programming），可直接用现成的优化计算包求解，但是利用拉格朗日乘子法可得到并进一步求解其对偶问题更加高效。


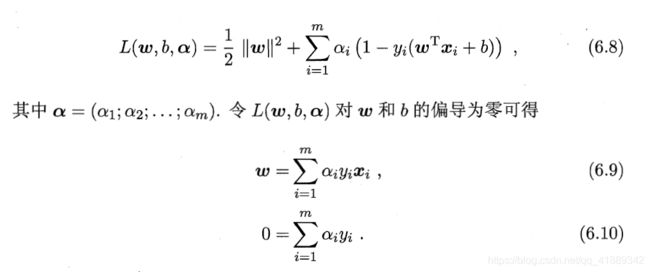
参考链接：拉格朗日乘子法和KKT条件

训练完成后，大部分的训练样本都不会保留，最终模型只与支持向量有关，模型复杂度与支持向量的数目有关。

（6.11）是一个二次规划问题，可使用通用的二次规划算法来求解，然而该问题的规模正比于训练样本数，这会在实际任务中造成很大的开销。为了避开这个障碍，人们利用问题本身的特性，提出了很多高效算法，例如SMO。SMO算法参考

6.3核函数

对于在原始空间中线性不可分的问题，可以将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分，

如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使得样本可分。

原始空间内划超平面所对应的模型为

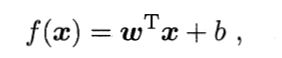
特征空间内划超平面所对应的模型为

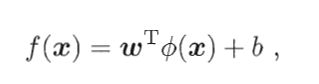
其对偶问题为

核函数（kernel function）为

对偶问题可重写成

求解得到支持向量展式（support vector expansion）

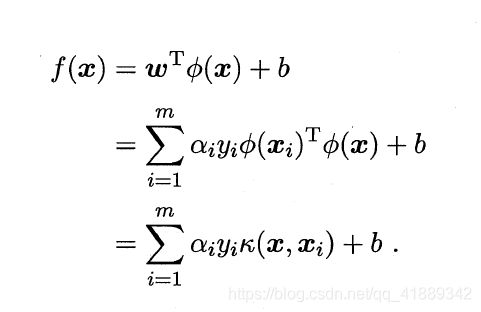
如何寻找核函数呢？

一个半正定核矩阵，总能找到一个与之对应的映射，换言之，任何一个核函数都隐式定义了一个称为“再生核希尔伯特空间”（Reproducing Kernel Hi了Bert Space）。

核函数的选择决定了支持向量机的性能。

文本数据经常采用线性核，情况不明时可先尝试高斯核。

核函数还可以通过函数组合得到。
（1）线性组合

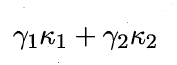
（2）核函数直积

（3）

6.4软间隔与正则化

在现实任务中，往往很难确定合适的核函数使得训练样本在特征空间中线性可分，即使恰好找到了某个核函数使得训练集在特种空间中线性可分，也很难断定这个可分的结果是不是由于过拟合造成的。

为了缓解上述问题的一个办法是允许支持向量机在一些样本上出错，为此引入软间隔（soft margin）

硬间隔（hard margin）：所有样本都必须分类正确

在最大化间隔的同时，不满足约束的样本应尽量少，优化目标可写为

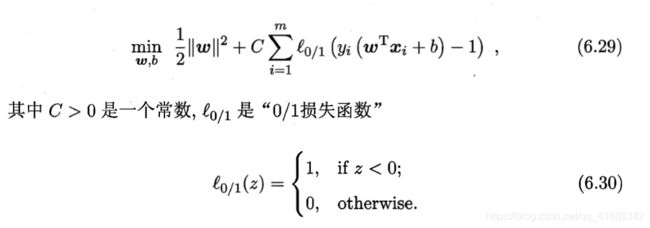
由于“0/1损失函数”的非凸、不连续，数学性质不太好，通常用其他函数来代替，称为替代损失（surrogate loss），替代函数一般具有很好的数学性质。

软间隔下的对偶问题

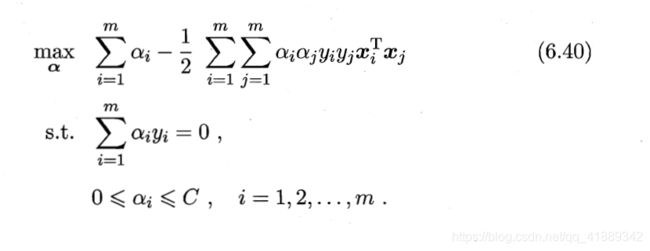
由KKT条件知，软间隔支持向量机的最终模型仅与支持向量有关（软间隔的支持向量或在间隔超平面上，或在间隔超平面之间，或在分类超平面的误分类一侧）

正则化问题（regularization）

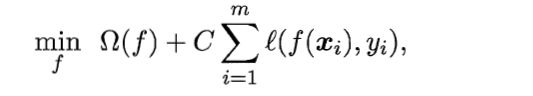
第一项是结构风险（structure risk），用于面熟模型$f$的某些性质；第二项是经验风险（empirical risk），用于描述模型与训练集的契合程度。$\Omega (f)$是正则化项，$C$是正则化常数。
L2范数是常用的正则化项。L2范数倾向于取值更加平衡，L0范数和L1范数倾向于更加稀疏。
正则化可以理解为一种罚函数法，对不希望得到的结果施以惩罚，从而使得优化过程趋向于希望目标，从贝叶斯估计的角度看，正则化可以认为是提供了模型的先验概率。

6.5支持向量回归

支持向量回归和传统回归的区别：传统回归模型当且仅当预测值和实际值相同时，损失才为零；支持向量回归（support vector regression，SVR）可以容忍一定的偏差，当预测值和实际值的偏差大于一定阈值时，才计算误差。


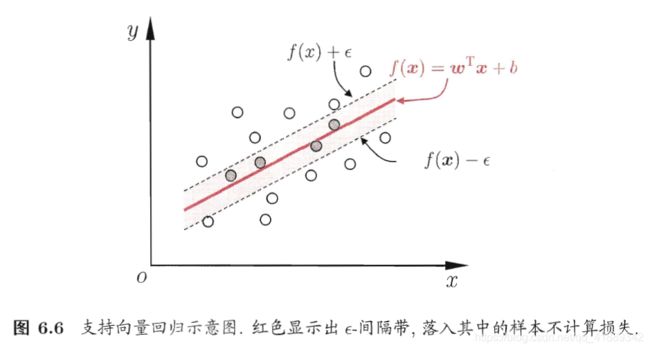
SVR的解形如：

SVR模型的支持向量是在隔离带之外的样本，SVR最终模型只与支持向量有关，其解仍具有稀疏性。

6.6核方法

若不考虑偏置项$b$，无论是SVM还是SVR都能表示成核函数的线性组合。

核方法（kernel methods）：基于核函数的学习方法，最常见的是通过“核化”（引入核函数）来将线性学习器拓展为非线性学习器

核函数直接决定了SVM和核方法的最终性能，但遗憾的是，核函数的选择是一个未决问题。

习题

6.1试证明样本空间中任意点$x$到超平面$(w,b)$的距离为式（6.2）

证明：
$$\begin{gathered} 设超平面为w^{T}x+b=0，则其法向量为w，空间中一点为x_1, \\ 设超平面上存在一点x_2，使得(x2-x1)与超平面垂直， \\ 则有(x_2-x_1)=\eta w(其中\eta \in R);(1) \\ 点x_1到超平面的距离为 \\ r=[(x_2-x_1{)}^T(x_2-x_1){]}^{\frac{1}{2}}=|\eta |\ast ||w|{|}_2;(2) \\ 根据点x_2在超平面上，有w^T{x}_2+b=0;(3) \\ 将(1)带入(3)，消掉x_2，得 \\ {w}^T{x}_1+b=-\eta ||w|{|}_2^2 \\ 两边取绝对值，得 \\ |w^T{x}_1+b|=|\eta |\ast ||w|{|}_2^2;(4) \\ 将(4)带入(2)得， \\ r=\frac{|w^T{x}_1+b|}{||w|{|}_2},原命题得证 \end{gathered}$$

6.2试使用LIBSVM，在西瓜数据集3.0$\alpha$上分别使用线性核和高斯核训练一个SVM，并比较其支持向量的差别

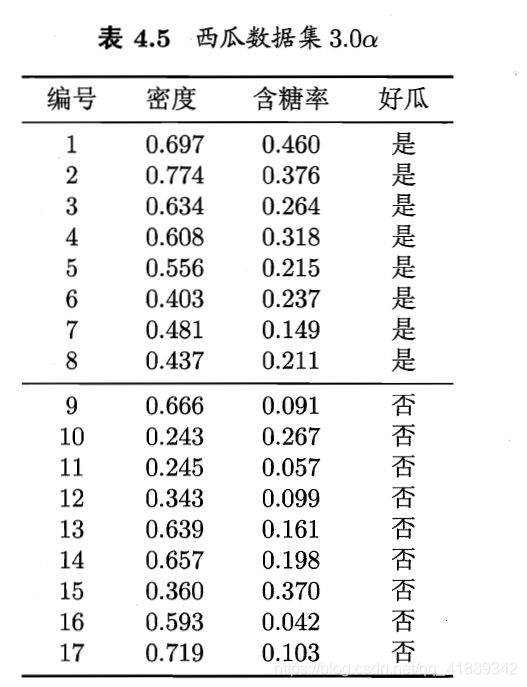
我使用的是sklearn的svm模块，也是基于libsvm的

from sklearn import svm
from sklearn.model_selection import cross_val_score

X=[
    [1.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.697, 0.46 ],
    [2.   , 2.   , 0.   , 0.   , 2.   , 1.   , 0.774, 0.376],
    [2.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.634, 0.264],
    [1.   , 2.   , 0.   , 0.   , 2.   , 1.   , 0.608, 0.318],
    [0.   , 2.   , 1.   , 0.   , 2.   , 1.   , 0.556, 0.215],
    [1.   , 1.   , 1.   , 0.   , 1.   , 0.   , 0.403, 0.237],
    [2.   , 1.   , 1.   , 1.   , 1.   , 0.   , 0.481, 0.149],
    [2.   , 1.   , 1.   , 0.   , 1.   , 1.   , 0.437, 0.211],
    [2.   , 1.   , 0.   , 1.   , 1.   , 1.   , 0.666, 0.091],
    [1.   , 0.   , 2.   , 0.   , 0.   , 0.   , 0.243, 0.267],
    [0.   , 0.   , 2.   , 2.   , 0.   , 1.   , 0.245, 0.057],
    [0.   , 2.   , 1.   , 2.   , 0.   , 0.   , 0.343, 0.099],
    [1.   , 1.   , 1.   , 1.   , 2.   , 1.   , 0.639, 0.161],
    [0.   , 1.   , 0.   , 1.   , 2.   , 1.   , 0.657, 0.198],
    [2.   , 1.   , 1.   , 0.   , 1.   , 0.   , 0.36 , 0.37 ],
    [0.   , 2.   , 1.   , 2.   , 0.   , 1.   , 0.593, 0.042],
    [1.   , 2.   , 0.   , 1.   , 1.   , 1.   , 0.719, 0.103]
]
y=[1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]

print("-"*20+"线性核"+"-"*20)
clf1=svm.SVC(C=1,kernel='linear')
print("交叉验证评分",cross_val_score(clf1,X,y,cv=5,scoring='accuracy').mean())
clf1.fit(X,y)
print("支持向量数目",clf1.n_support_.sum())
print("支持向量",clf1.support_vectors_)

print("-"*20+"高斯核"+"-"*20)
clf2=svm.SVC(C=1,kernel='rbf')
print("交叉验证评分",cross_val_score(clf2,X,y,cv=5,scoring='accuracy').mean())
clf2.fit(X,y)
print("支持向量数目",clf2.n_support_.sum())
print("支持向量",clf2.support_vectors_)

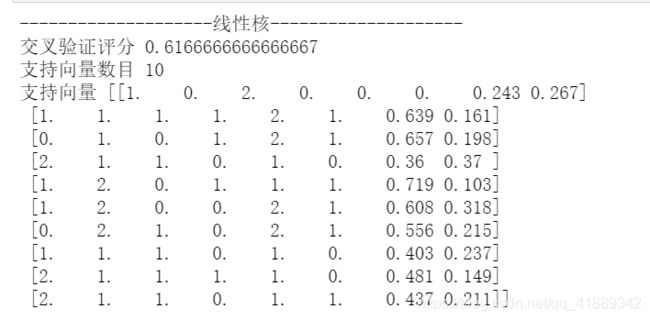
简单分析：在其他参数相同的情况下，在交叉验证评分上，高斯核svm要高于线性核svm；在模型复杂度上，高斯核svm的支持向量的数目要多于线性核svm，因此高斯核svm更加复杂

6.3选择两个UCI数据集，分别用线性核和高斯核训练一个SVM，并与BP神经网络和C4.5决策树进行比较

6.4试讨论线性判别分析与线性核支持向量机在何种条件下等价

1. LDA和线性SVM都希望能最大化异类样例间距，但LDA是异类中心间距最大化，而线性SVM考虑的是支持向量间距最大
2. LDA的目标函数考虑了同类样例的协方差，希望同类样例在投影空间尽可能靠近，而线性SVM却没有考虑这一点。
3. 关于数据是否线性可分的问题，如果使用软间隔的线性SVM，线性可分这个条件是不必要的，如果是硬间隔线性SVM，那么线性可分是必要条件。但是LDA不管数据是否线性可分，都可以进行处理
4. 假如当前样本线性可分，且SVM与LDA求出的结果相互垂直。则当SVM的支持向量固定时，再加入新的非支持向量样本，并不会改变SVM中求出的w。但是新加入的样本会改变原类型数据的协方差和均值，从而导致LDA求出的结果发生改变。这个时候两者的w就不再垂直，但是数据依然是可分的。所以， 线性可分 和 LDA求出的wl与线性核支持向量机求出的ws垂直，这两个条件是不等价的。
5. 所以，该题的答案严格上来讲，应该是当线性SVM和LDA求出的w互相垂直时，两者是等价的。因为一般LDA是不带偏置项的（因为LDA的思想是投影，投影过程和偏置是没有任何关系的），所以SVM这个时候比LDA仅仅多了个偏移b。
   参考：https://blog.csdn.net/qq_37691909/article/details/85630937

6.5试述高斯核SVM和RBF神经网络之间的联系

若将隐层神经元的数目设置为训练样本数，且每个训练样本对应一个神经元中心，则RBF网络的预测函数与高斯核SVM的预测函数相同。但是，这也只是形式相同而已，两种方法还是存在着本质区别的，比如RBF的样本中心是通过聚类等方法获得的，而高斯核RBF直接定义成每条样本；RBF函数的参数是通过学习得到的，而高斯核的参数是手动设置的。

6.6试分析SVM对噪声敏感的原因

SVM 的特性就是 “支持向量” . 即线性超平面只由少数 “支持向量” 所决定. 若噪声成为了某个 “支持向量” —— 这是非常有可能的. 那么对整个分类的影响是巨大的. 反观对率回归, 其线性超平面由所有数据共同决定, 因此一点噪声并无法对决策平面造成太大影响.
参考：https://www.cnblogs.com/cloud–/p/12304663.html