西瓜书《机器学习》读书笔记-第6章 支持向量机(Support Vector Machine)

写在前面
开始挖新坑学习一下《机器学习》. 主要是看浙江大学胡浩基老师的网课，结合周志华老师的西瓜书来学. 为了理清思路和推公式就敲了这样一个读书笔记. 初次学习难免会有错漏，欢迎批评指正. 这份笔记主要用途还是用来自己复习回顾. 当然如果对大家有帮助那就更好了hhh

第6章 支持向量机(Support Vector Machine)

· 提出者：$\text{Vladimir N. Vapnik}$.
· 在样本数量较小时，效果较好. 其背后具有有力的数学原理支撑.
· 相关书籍：《支持向量机导论》.

概念

1. 线性可分(Linear Separable)
2. 非线性可分（Non-linear Separable）

线性可分样本集可以用无线条直线将两种类别的样本划分开，那么哪条直线划分效果最好？

3. 定义“性能指标”，性能指标越高，则划分效果越好. 如下图所示，性能指标定义为间隔$\gamma$.
   

数学描述

1. $d$：间隔(margin)

支持向量机是使得$d$最大的方法（$\text{SVM}$是最大化间隔的分类算法）

2. 支持向量(support vector)：平行线“插”到的向量

一、 概念与定义

1. 训练数据及标签：$({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_n,y_n)$
   其中${\mathbf{x}}_i$为向量，$y_i\in \left\{-1,+1\right\}$为标签.
2. 线性模型：

需要找到一个模型，在二维情形为直线，三维情形为平面，多维情形为超平面. 其参数为$(\mathbf{w},b)$

考虑超平面(Hyperplane):
$${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$$其中
$$\mathbf{w}={\left[\begin{array}{cccc}{w}_1& w_2& \cdots & w_N\end{array}\right]}^{\mathrm{T}}$$是超平面的法向量.

3. 一个训练集线性可分：
   $$\begin{gathered} \exists \left(\mathbf{w},b\right),\text{使}\forall i=1,\cdots ,N,\text{有}\{\begin{array}{c}\left(a\right)\text{若}{y}_i=+1,\text{则}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾0\\ \left(b\right)\text{若}{y}_i=-1,\text{则}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b<0\end{array} \\ \left(\text{或}{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾0\right) \end{gathered}$$

二、支持向量机的基本型

由上述推导可知，$\text{SVM}$是要解决以下的优化问题:
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\min }{\Vert \mathbf{w}\Vert }^2\\ & \mathrm{s}.\mathrm{t}.y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\cdots ,N.\end{array}$$

一些事实：
事实1：${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$与$a{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+ab=0$表示同一个平面. （$a\in {\mathbb{R}}^{+}$）
该事实蕴含：
若$\left(\mathbf{w},b\right)$满足公式1，则$\left(a\mathbf{w},ab\right)$也满足公式1.
事实2：点${\mathbf{x}}_0$到超平面${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$距离
$$r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right|}{\Vert \mathbf{w}\Vert }$$

1. 关于最小化目标函数的解释

我们可以用$a(a>0)$去缩放$\left(\mathbf{w},b\right)\to \left(a\mathbf{w},ab\right)$，最终使在支持向量${\mathbf{x}}_0$上，有
$$\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right|=1$$

具体地说，通过平移超平面${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$，可以得到一系列与其平行的平面${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=m$. 不妨设当平面穿过支持向量${\mathbf{x}}_0$时，有${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b=m_0$. 为了便于计算，将等式右边化为$1$，即
$$\frac{1}{m_0}\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right)=1$$那么此时由于
$${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b=0\iff \frac{1}{m_0}\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right)=0$$
这两个方程表示同一个超平面，因此可作变换$\left({\mathbf{w}}^{\mathrm{T}},b\right):=\frac{1}{m_0}\left({\mathbf{w}}^{\mathrm{T}},b\right).$

此时，支持向量与平面距离
$$r=\frac{1}{\Vert \mathbf{w}\Vert }$$我们需要最大化$r$，也即最小化${\Vert \mathbf{w}\Vert }^2$.

2. 关于限制条件的解释

对于支持向量以外的向量，其与平面距离不小于$r$，即
$$\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right|}{\Vert \mathbf{w}\Vert }⩾r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right|}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert }$$即
$$\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right|⩾1$$具体来说，对于在平面上、下方的向量，有
$$\{\begin{array}{c}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾1,{\mathbf{x}}_i\text{在平面上方}\\ -{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾1,{\mathbf{x}}_i\text{在平面下方}\end{array}\iff y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1$$

3. 目标函数的写法

$\underset{\mathbf{w},b}{\min }{\Vert \mathbf{w}\Vert }^2$ 也可以写作$\underset{\mathbf{w},b}{\min }\frac{1}{2}{\Vert \mathbf{w}\Vert }^2$，其中的$\frac{1}{2}$是为了方便求导.

4. 这是一个凸二次规划(convex quadratic programming) 问题

附：二次规划问题(Quadratic Programming)
（1）目标函数(objective function)：二次项
（2）限制条件：一次项

显然目标函数全为二次项，限制条件为一次项，属于二次规划问题.
事实：二次规划中，要么无解，要么只有一个极值. 因此，支持向量机的理论将寻找超平面的问题转化为了能够求得全局最优解的二次规划问题.
至于如何求解这个二次规划问题，需要凸优化理论，在此处不涉及.

三、支持向量机的非线性模型

目的：使得训练样本是非线性可分时也有解.

（一）改写优化目标函数和限制条件

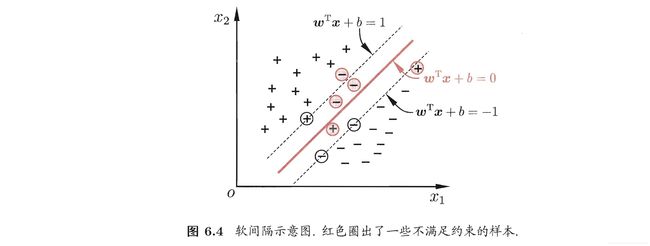
1. 软间隔(soft margin)

引入软间隔，从而允许支持向量机在部分样本上出错.

2. 优化问题的改写

$$\underset{\mathbf{w},b}{\min }\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^N{l}_{0/1}\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)$$其中常数$C>0$，$0/1$损失函数
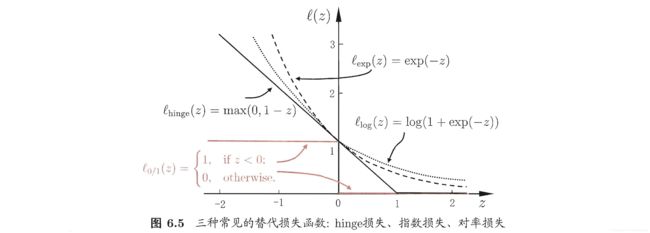
$$l_{0/1}\left(z\right)=\{\begin{array}{l}1,\mathrm{i}\mathrm{f}z<0；\\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}$$

3. 替代损失函数(surrogate loss)

$0/1$损失函数$l_{0/1}$性质不好，用其他函数替代.

4. 软间隔支持向量机

采用$\text{hinge}$损失，有
$$\sum _{i=1}^N{l}_{0/1}\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)=\sum _{i=1}^N\max \left(0,1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\right)$$引入松弛变量${\xi }_i$. 令
$$\max \left(0,1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\right)={\xi }_i$$显然有${\xi }_i⩾0$. 并且当$1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)>0$时，有
$$1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)={\xi }_i$$当$1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩽0$时
$${\xi }_i=0$$因此
$$1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩽{\xi }_i\Rightarrow y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i$$从而将问题转化为
$$\begin{array}{rl}& \underset{\mathbf{w},b,{\xi }_i}{\min }\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^N{\xi }_i\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{l}{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ {\xi }_i⩾0\end{array}\end{array}$$

关于松弛变量(slack variables)的说明
(1) 当${\xi }_i$非常大的时候，虽然限制条件1容易被满足，但优化问题得到的解并不理想. 因此，在目标函数中增加一项$C{\sum }_{i=1}^N{\xi }_i$，使得${\xi }_i$不至于太大.
(2) 其中$C{\sum }_{i=1}^N{\xi }_i$称作正则项(regularization term)（或称作惩罚系数）. $C$为事先设定好的参数，其选取方法为在一定的区间内尝试不同的$C$，选择效果较好的那个$C$. （这也是$\text{SVM}$算法表现较好的原因，因为需要调整的参数少）

（二）低维到高维的映射

1.【引入】异或问题

在较低维度下，训练样本非线性可分. 考虑将训练样本映射到更高维的空间中，再进行划分. 即
$$\mathbf{x}\mapsto \varphi \left(\mathbf{x}\right)$$将低维的$\mathbf{x}$映射到高维$\phi \left( \boldsymbol{x} \right) $，再用平面进行划分.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gMdFYc98-1626697939749)(2021-07-18-16-34-13.png)]
考虑一个具体问题：平面上有四点
$$x_1=\left[\begin{array}{c}0\\ 0\end{array}\right]\in C_1,x_2=\left[\begin{array}{c}1\\ 1\end{array}\right]\in C_1,x_3=\left[\begin{array}{c}1\\ 0\end{array}\right]\in C_2,x_4=\left[\begin{array}{c}0\\ 1\end{array}\right]\in C_2.$$定义$\varphi (x)$：
$$x=\left[\begin{array}{c}a\\ b\end{array}\right]\stackrel{\varphi }{}\varphi \left(x\right)=\left[\begin{array}{c}{a}^2\\ b^2\\ a\\ b\\ ab\end{array}\right]$$那么
$$\begin{gathered} \varphi \left(x_1\right)={\left[\begin{array}{ccccc}0& 0& 0& 0& 0\end{array}\right]}^{\mathrm{T}}\in C_1,\varphi \left(x_2\right)={\left[\begin{array}{ccccc}1& 1& 1& 1& 1\end{array}\right]}^{\mathrm{T}}\in C_1, \\ \varphi \left(x_3\right)={\left[\begin{array}{ccccc}1& 0& 1& 0& 0\end{array}\right]}^{\mathrm{T}}\in C_2,\varphi \left(x_4\right)={\left[\begin{array}{ccccc}0& 1& 0& 1& 0\end{array}\right]}^{\mathrm{T}}\in C_2. \end{gathered}$$取
$$\mathbf{w}={\left[\begin{array}{ccccc}-1& -1& -1& -1& 6\end{array}\right]}^{\mathrm{T}}（不唯一）$$有
$$\{\begin{array}{l}\begin{array}{r}{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_1\right)+b=1\\ {\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_2\right)+b=3\end{array}\}\in C_1\\ \begin{array}{r}{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_3\right)+b=-1\\ {\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_4\right)+b=-1\end{array}\}\in C_2\end{array}$$

那么$\varphi (\mathbf{x})$应如何选取？关于$\varphi (\mathbf{x})$，有以下事实：
① 我们认为选定的$\varphi (\mathbf{x})$是无限维的.
② 我们可以不知道无限维映射$\varphi (\mathbf{x})$的显式表达，而只需知道一个核函数（kernel function）
$$\kappa ({\mathbf{x}}_1,{\mathbf{x}}_2)=\varphi ({\mathbf{x}}_1{)}^{\mathrm{T}}\varphi ({\mathbf{x}}_2)=⟨\varphi \left({\mathbf{x}}_1\right),\varphi \left({\mathbf{x}}_2\right)⟩$$则该优化问题仍然可解.

2. 常用核函数

注：
1.多项式核的幂次$d$越高，其对应的$\varphi$维数也越高. 且多项式核可反解出$\varphi$.
2. 参数选择：不断尝试.

3. $\kappa ({\mathbf{x}}_1,{\mathbf{x}}_2)$ 能写成 $\varphi ({\mathbf{x}}_1{)}^{\mathrm{T}}\varphi ({\mathbf{x}}_2)$的充要条件：Merce’s Theorem

（1）交换性

$$\kappa \left({\mathbf{x}}_1,{\mathbf{x}}_2\right)=\kappa \left({\mathbf{x}}_2,{\mathbf{x}}_1\right)$$

（2）半正定性

$$\forall c_i,{\mathbf{x}}_i\left(i=1,2,\cdots ,N\right),\text{有}\sum _{i=1}^N\sum _{i=1}^N{c}_i{c}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)⩾0$$

注：以上两条也可写作：$\kappa$是核函数，当且仅当对任意数据$D=\left\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_m\right\}$，“核矩阵”$\mathbf{K}$总是半正定的. 其中

附：半正定性表达式的推导
半正定即
$$\begin{gathered} \forall C=\left[\begin{array}{c}{c}_1\\ ⋮\\ c_n\end{array}\right]\ne 0,C_{1\times n}^{\mathrm{T}}{\mathbf{K}}_{n\times n}{C}_{n\times 1}⩾0\iff \\ {\left({\mathbf{K}}_{n\times n}{C}_{n\times 1}\right)}_i=\sum _{j=1}^n{c}_j\kappa \left(i,j\right) \\ {C}_{1\times n}^{\mathrm{T}}{\mathbf{K}}_{n\times n}{C}_{n\times 1}=c_1\sum _{j=1}^n{c}_j\kappa \left(1,j\right)+\cdots +c_n\sum _{j=1}^n{c}_j\kappa \left(n,j\right) \\ =\sum _{i=1}^n\sum _{j=1}^n{c}_i{c}_j\kappa \left(i,j\right) \end{gathered}$$

4. 核函数的选取

P128 “核函数选择”成为支持向量机的最大变数. 这方面有一些基本的经验，例如对文本数据通常采用线性核，情况不明时可先尝试高斯核.

核函数还可通过函数组合得到，详见西瓜书P128.

那么，如何用核函数$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$来替换目标函数中的$\varphi ({\mathbf{x}}_i)$，使得优化问题可解？

（三）【补充】优化理论相关知识——原问题和对偶问题

优化理论相关书籍：① Convex Optimization；② Nonlinear Programming

1. 原问题（Primal Problem）

$$\begin{array}{rl}& \min f\left(\mathbf{w}\right)\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{c}{g}_i\left(\mathbf{w}\right)⩽0\left(i=1,\cdots ,K\right)\\ h_i\left(\mathbf{w}\right)=0\left(i=1,\cdots ,M\right)\end{array}\end{array}$$

2. 对偶问题(Dual Problem)

定义$$\begin{array}{rl}L\left(\mathbf{w},\mathbf{\alpha },\mathbf{\beta }\right)& =f\left(\mathbf{w}\right)+\sum _{i=1}^K{\alpha }_i{g}_i\left(\mathbf{w}\right)+\sum _{i=1}^M{\beta }_i{h}_i\left(\mathbf{w}\right)\\ & =f\left(\mathbf{w}\right)+{\mathbf{\alpha }}^{\mathrm{T}}g\left(\mathbf{w}\right)+{\mathbf{\beta }}^{\mathrm{T}}h\left(\mathbf{w}\right)\end{array}$$

原问题的对偶问题为
$$\begin{array}{rl}& \max \Theta \left(\mathbf{\alpha },\mathbf{\beta }\right)=\underset{\text{所有}\mathbf{w}}{\inf }\left(L\left(\mathbf{w},\mathbf{\alpha },\mathbf{\beta }\right)\right)\\ & \mathrm{s}.\mathrm{t}.{\alpha }_i⩾0\left(i=1,\cdots ,K\right)\left(\text{或写作}\mathbf{\alpha }\succcurlyeq 0\right)\end{array}$$

3. 原问题和对偶问题的关系

定理：如果${\mathbf{w}}^{\ast }$是原问题的解，${\mathbf{\alpha }}^{\ast }$,${\mathbf{\beta }}^{\ast }$是对偶问题的解，则有$$f\left({\mathbf{w}}^{\ast }\right)⩾\Theta \left({\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right).$$

证明：
$$\begin{array}{rl}\Theta \left({\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)& =\mathrm{i}\mathrm{n}\mathrm{f}\left(L\left(\mathbf{w},{\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)\right)\\ & ⩽L\left({\mathbf{w}}^{\ast },{\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)\\ & =f\left({\mathbf{w}}^{\ast }\right)+\sum _{i=1}^K{\alpha }_i^{\ast }{g}_i\left({\mathbf{w}}^{\ast }\right)+\sum _{i=1}^M{\beta }_i^{\ast }{h}_i\left({\mathbf{w}}^{\ast }\right)\\ & ⩽f\left({\mathbf{w}}^{\ast }\right)\left(\text{注意到}{\alpha }_i^{\ast }⩾0,g_i\left({\mathbf{w}}^{\ast }\right)⩽0,h_i\left({\mathbf{w}}^{\ast }\right)=0\right)\end{array}$$

4. 定义：原问题与对偶问题的间距(duality gap)s

$G=f\left({\mathbf{w}}^{\ast }\right)-\Theta \left({\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)⩾0$，$G$叫作原问题与对偶问题的间距(duality gap). 对于某些特定的优化问题，可以证明$G=0$.

5. 强对偶定理

若$f(\mathbf{w})$是凸函数，且$g(\mathbf{w})=A\mathbf{w}+b$, $h(\mathbf{w})=C\mathbf{w}+d$，则此优化问题的原问题与对偶问题的间距$G=0$，即
$$f\left({\mathbf{w}}^{\ast }\right)=\Theta \left({\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right).$$

$f\left({\mathbf{w}}^{\ast }\right)=\Theta \left({\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)$蕴含：
① 原问题的解${\mathbf{w}}^{\ast }$是${\mathbf{\alpha }}^{\ast }$和${\mathbf{\beta }}^{\ast }$一定时，使得$L\left(\mathbf{w},{\mathbf{\alpha }}^{\ast },{\mathbf{\beta }}^{\ast }\right)$最小的那个$\mathbf{w}$.
② KKT条件：对于$\forall i=1,2,\cdots ,K$，或者${\alpha }_i^{\ast }=0$，或者$g_i\left({\mathbf{w}}^{\ast }\right)=0$.

（四）将支持向量机原问题转化为对偶问题

1. 问题的转换

原问题：

$$\begin{array}{rl}& \min \frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^N{\xi }_i（容易知道，这是一个凸函数）\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{l}{y}_i\left({\mathbf{w}}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b\right)⩾1-{\xi }_i\\ {\xi }_i⩾0\end{array}\end{array}$$

原问题的标准型：

$$\begin{array}{rl}& \min \frac{1}{2}{\Vert \mathbf{w}\Vert }^2-C\sum _{i=1}^N{\xi }_i\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{l}1+{\xi }_i-y_i\left({\mathbf{w}}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b\right)⩽0\\ {\xi }_i⩽0\end{array}\end{array}$$

凸函数定义：
$$\forall {\mathbf{w}}_1,{\mathbf{w}}_2,\forall \lambda \in \left[0,1\right],f\left(\lambda {\mathbf{w}}_1+\left(1-\lambda \right){\mathbf{w}}_2\right)⩽\lambda f\left({\mathbf{w}}_1\right)+\left(1-\lambda \right)f\left({\mathbf{w}}_2\right)$$

对偶问题:

$$\begin{array}{rl}& \max \Theta \left(\mathbf{\alpha },\mathbf{\beta }\right)=\mathrm{i}\mathrm{n}\mathrm{f}\left(\frac{1}{2}{\Vert \mathbf{w}\Vert }^2-C\sum _{i=1}^N{\xi }_i+\sum _{i=1}^N{\beta }_i{\xi }_i+\sum _{i=1}^N{\alpha }_i\left(1+{\xi }_i-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b\right)\right)\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{c}{\alpha }_i⩾0\\ {\beta }_i⩾0\end{array}\left(i=1,2,\cdots ,N\right)\end{array}$$

附：矩阵求导法则
$$\begin{array}{rl}& ①\mathbf{w}=\left[\begin{array}{c}{w}_1\\ ⋮\\ w_n\end{array}\right],\text{则}\frac{\partial f}{\partial \mathbf{w}}=\left[\begin{array}{c}\frac{\partial f}{\partial w_1}\\ ⋮\\ \frac{\partial f}{\partial w_n}\end{array}\right].\\ & ②f\left(\mathbf{w}\right)=\frac{1}{2}{\Vert \mathbf{w}\Vert }^2=\frac{1}{2}\sum _{i=1}^n{w}_i^2,\text{则}\frac{\partial f}{\partial \mathbf{w}}=\left[\begin{array}{c}\frac{\partial f}{\partial w_1}\\ ⋮\\ \frac{\partial f}{\partial w_n}\end{array}\right]=\left[\begin{array}{c}{w}_1\\ ⋮\\ w_n\end{array}\right]=\mathbf{w}\\ & ③f\left(\mathbf{w}\right)={\mathbf{w}}^{\mathrm{T}}\mathbf{x}=\sum _{i=1}^n{w}_i{x}_i,\text{则}\frac{\partial f}{\partial \mathbf{w}}=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right]=\mathbf{x}\end{array}$$

利用$\text{Lagrange}$乘子法，先求得$\frac{1}{2}{\Vert \mathbf{w}\Vert }^2-C{\sum }_{i=1}^N{\xi }_i+{\sum }_{i=1}^N{\beta }_i{\xi }_i+{\sum }_{i=1}^N{\alpha }_i\left(1+{\xi }_i-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b\right)$取得最小值时各参数应满足的条件.
$$\{\begin{array}{l}\frac{\partial L}{\partial \mathbf{w}}=0\Rightarrow \mathbf{w}={\sum }_{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)\\ \frac{\partial L}{\partial {\xi }_i}=0\Rightarrow {\alpha }_i+{\beta }_i=C\\ \frac{\partial L}{\partial b}=0\Rightarrow {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}$$然后将上述三个条件代入$\Theta \left(\mathbf{\alpha },\mathbf{\beta }\right)$.

具体推导步骤如下
$$\begin{array}{rl}& \Theta \left(\mathbf{\alpha },\mathbf{\beta }\right)=\frac{1}{2}{\Vert \mathbf{w}\Vert }^2-C\sum _{i=1}^N{\xi }_i+\sum _{i=1}^N{\beta }_i{\xi }_i+\sum _{i=1}^N{\alpha }_i\left(1+{\xi }_i-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b\right)\\ & \stackrel{{\alpha }_i+{\beta }_i=C}{}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+\sum _{i=1}^N{\alpha }_i\left(1-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b\right)\\ & \stackrel{{\sum }_{i=1}^N{\alpha }_i{y}_i=0}{}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & \stackrel{\mathbf{w}={\sum }_{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)}{}\frac{1}{2}{\left(\sum _{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)\right)}^{\mathrm{T}}\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi \left({\mathbf{x}}_j\right)\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & \stackrel{{\left({\sum }_{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)\right)}^{\mathrm{T}}={\sum }_{i=1}^N{\alpha }_i{y}_i\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}}{}\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & \stackrel{\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)}{}\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & \stackrel{\mathbf{w}={\sum }_{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)}{}\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\left(\sum _{j=1}^N{\alpha }_j{y}_j\varphi \left({\mathbf{x}}_j\right)\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi {\left({\mathbf{x}}_j\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)\\ & \stackrel{\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\kappa \left({\mathbf{x}}_j,{\mathbf{x}}_i\right)=\varphi {\left({\mathbf{x}}_j\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)}{}\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\\ & =\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\end{array}$$

问题转化为
$$\begin{array}{rl}& \max \Theta \left(\mathbf{\alpha }\right)=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{l}0⩽{\alpha }_i⩽C\left(\text{由}{\alpha }_i+{\beta }_i=C\wedge {\alpha }_i⩾0\wedge {\beta }_i⩾0\right)\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}\end{array}$$
可使用SMO(Sequential Minimal Optimization)算法求解.

附：SMO的基本思路（西瓜书P124）



至此，我们求得了$\mathbf{\alpha }$.

在最开始的问题中，我们需要求得$\mathbf{w}$和$b$. 但事实上，我们并不需要求得$\mathbf{w}$，具体说明如下：

2. $\mathbf{w}$如何求解？

先看以下的训练集测试流程.

输入测试样本$\mathbf{x}$：
$$\{\begin{array}{c}\mathrm{i}\mathrm{f}{\mathbf{w}}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b⩾0:y=+1\\ \mathrm{i}\mathrm{f}{\mathbf{w}}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b<0:y=-1\end{array}$$

注意到
$${\mathbf{w}}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b={\left(\sum _{i=1}^N{\alpha }_i{y}_i\varphi \left({\mathbf{x}}_i\right)\right)}^{\mathrm{T}}\varphi \left(\mathbf{x}\right)+b=\sum _{i=1}^N{\alpha }_i{y}_i\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)+b$$

因此无需知道$\mathbf{w}$和$\varphi$的显式表达式，即可完成训练样本的分类.

3. $b$ 如何求解？

根据KKT条件
$$\{\begin{array}{l}\text{要么}{\beta }_i=0,\text{要么}{\xi }_i=0\\ \text{要么}{\alpha }_i=0,\text{要么}1+{\xi }_i-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b=0\end{array}$$故有
$${\beta }_i=C-{\alpha }_i>0\Rightarrow {\beta }_i\ne 0\Rightarrow {\xi }_i=0$$又${\alpha }_i\ne 0$，有
$$\begin{array}{rl}1+{\xi }_i-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)-y_{i}b& =0\\ \Rightarrow b=\frac{1-y_i{\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)}{y_i}& =\frac{1-y_i{\sum }_{j=1}^N{\alpha }_j{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)}{y_i}\end{array}$$可以使用所有支持向量求解$b$的平均值.

至此，完成了$\text{SVM}$非线性模型的求解.

（五）$\text{SVM}$的非线性模型总结

1. 训练流程

$Step1:$输入$\left({\mathbf{x}}_i,y_i\right)\left(i=1,2,\cdots ,N\right)$.

$Step2:$解优化问题.
$$\begin{array}{rl}& \max \Theta \left(\mathbf{\alpha }\right)=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\\ & \mathrm{s}.\mathrm{t}.\{\begin{array}{l}0⩽{\alpha }_i⩽C\left(\text{由}{\alpha }_i+{\beta }_i=C\wedge {\alpha }_i⩾0\wedge {\beta }_i⩾0\right)\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}\end{array}$$
$Step3:$计算$b$.
找一个$0<{\alpha }_i<C$，则
$$b=\frac{1-y_i{\sum }_{j=1}^N{\alpha }_j{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)}{y_i}$$

2. 测试流程

输入测试样本$\mathbf{x}$：
$$\{\begin{array}{l}\mathrm{i}\mathrm{f}{\sum }_{i=1}^N{\alpha }_{i}y\end{array}$$