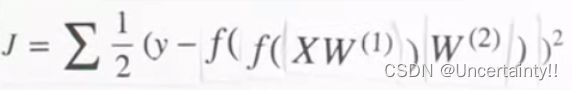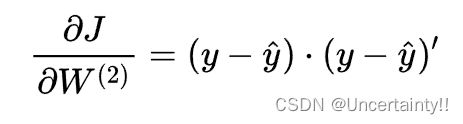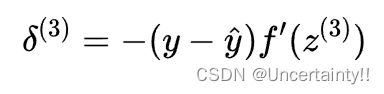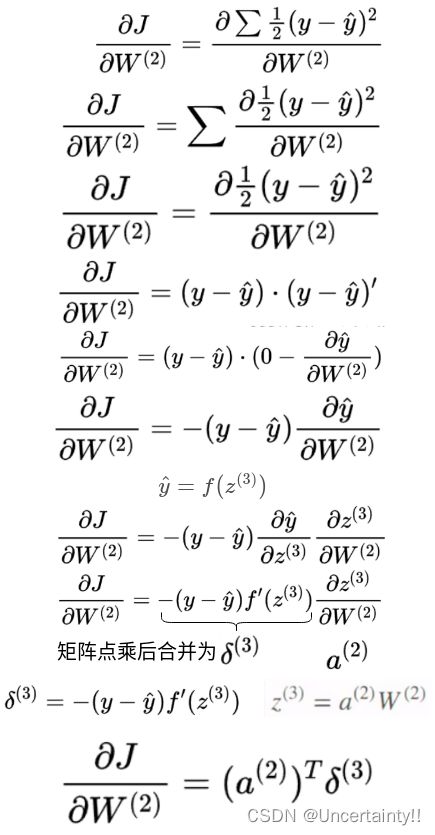神经网络入门(上)
神经网络入门
- 神经网络入门(上)
-
- 1.1 构建神经网络
-
- 1.1.1 前向传播(Forward Propagation)
- 1.1.2 梯度下降(Gradient Descent) and 反向传播(Back Propagation)
- 1.1.3 数值梯度检验(Numerical Gradient Checking)
- 1.2 训练神经网络
- 1.3 测试神经网络
神经网络入门(上)
笔记来源:Neural Networks Demystified
声明:本人为小白,第一次学习有关知识,本篇为学习笔记,如有错误,请各位大佬匹配指正!
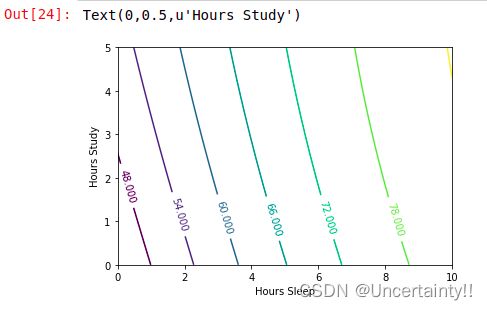
我们现在做个简单预测,由考前睡眠时间(Hours sleep)和考前学习时间(Hours study)来预测考试分数(Score on test)
只是演示,仅仅给出了三组样本值
考前睡眠时间(Hours sleep)和考前学习时间(Hours study)构成矩阵 X X X
考试分数(Score on test)构成矩阵 Y Y Y
1.1 构建神经网络
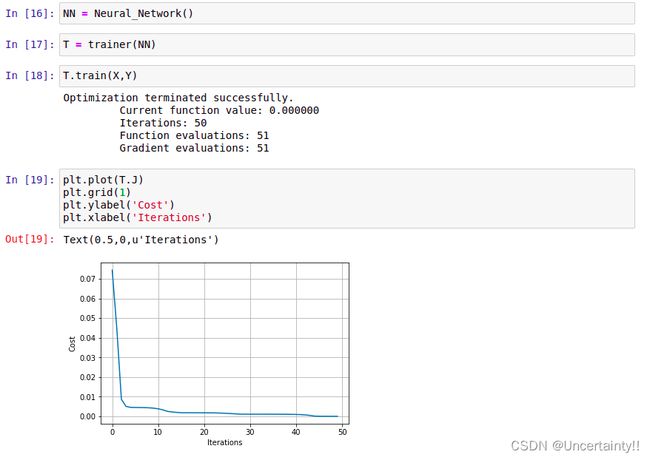
导入库
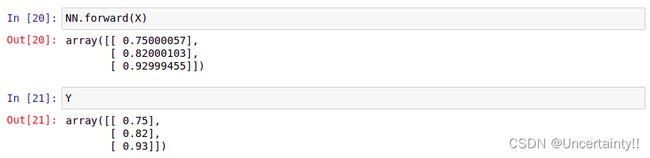
 导入样本数据
导入样本数据

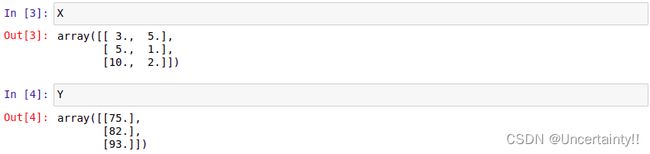 我们将输入样本数据缩放到0到1之间
我们将输入样本数据缩放到0到1之间
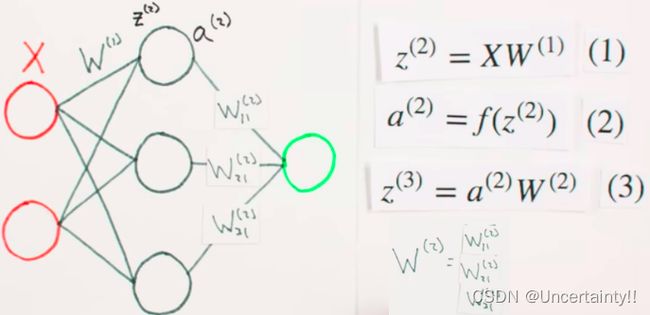
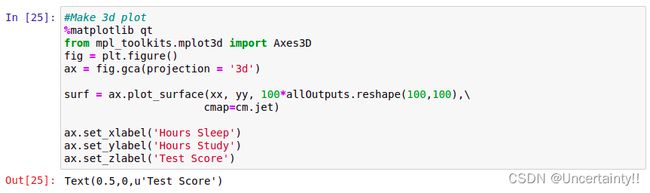
 神经网络大致形态
神经网络大致形态
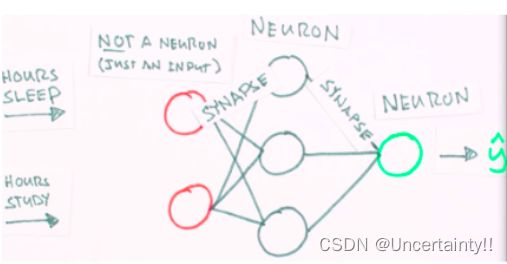

输入层神经元个数:2
输出层神经元个数:1
隐藏层神经元个数:3
输入层与隐藏层间的权值矩阵W1(由随机数生成,可能用到正态分布)
隐藏层与输出层间的权值矩阵W2(由随机数生成,可能用到正态分布)
1.1.1 前向传播(Forward Propagation)
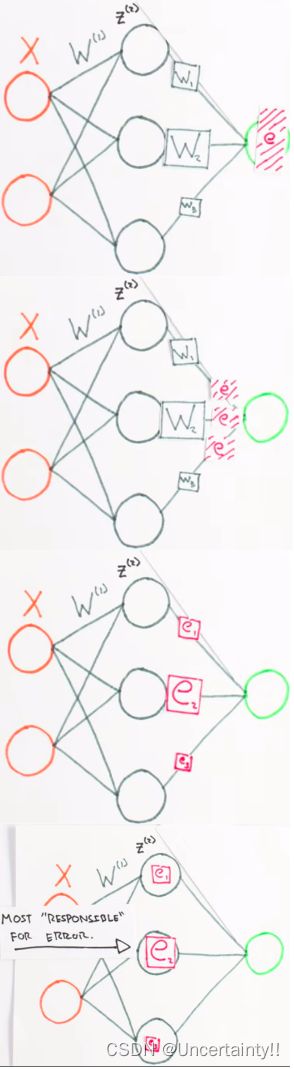
先将样本数据一行一行依次放入输入层,如下图,先将样本数据第一行第一个数3放入输入层上面的神经元,然后将3分别乘上3个权值,将三个结果放入隐藏层,然后将样本数据第一行第二个数5放入输入层下面的神经元,然后将5分别乘上3个权值,将三个结果放入隐藏层,将此结果与前面的结果进行加和
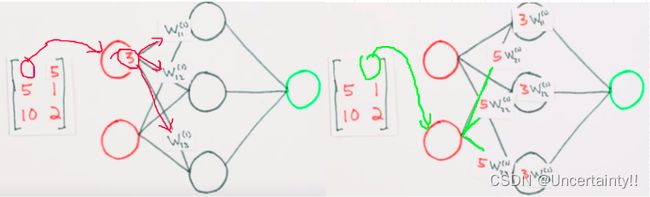
上面描述的过程,其实就是将样本数据组成的矩阵 X X X与权值组成的矩阵 W ( 1 ) W^{(1)} W(1) (代表第一层权值构成的矩阵)点乘的结果
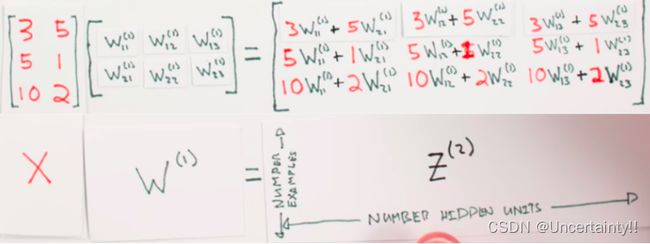
将上述矩阵 Z ( 2 ) Z^{(2)} Z(2)中每一行作为Sigmoid函数的输入,也就是隐藏层的输入,经过Sigmoid计算得出的结果作为隐藏层的输出


将隐藏层中各个神经元的输出再与各权值相乘,随后相加作为输出层的输入,同时也是输出层的输出
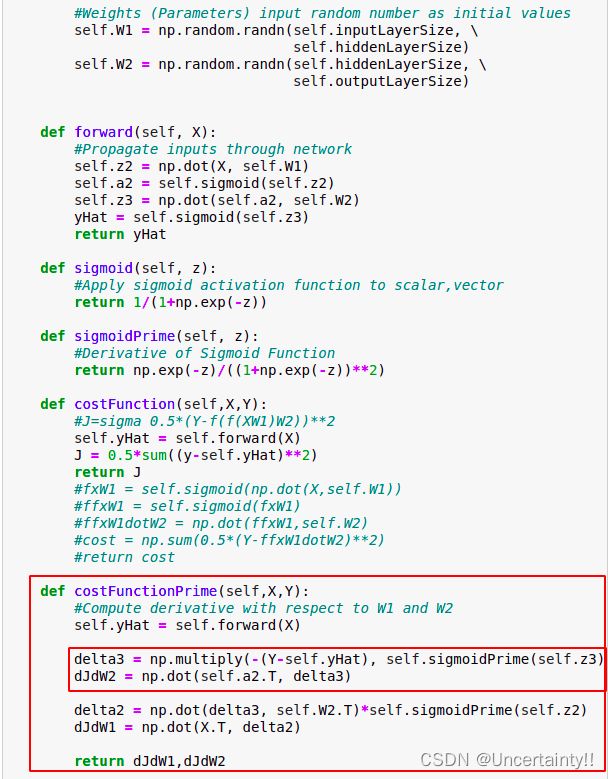
前向传播:
输入值矩阵X与权值矩阵W1点乘
将点乘结果送入Sigmoid处理,处理结果作为隐藏层的输出
将隐藏层的输出与权值矩阵W2点乘,处理结果作为输出层的输入,亦即输出层的输出
将输出层的输出赋值给 y ^ \hat{y} y^ 作为估计值的初始值
将此估计值送入最小二乘,通过计算得到最小值,也就是最小误差,我们也就完成了训练神经网络的目的
| 参数 | 含义 |
|---|---|
| X | 输入向量 |
| W ( 1 ) W^{(1)} W(1) | 输入层与隐藏层间的权值矩阵W1 |
| Z ( 2 ) Z^{(2)} Z(2) | 隐藏层的输入 |
| f | Sigmoid激活函数 |
| a ( 2 ) a^{(2)} a(2) | 隐藏层的输出向量 |
| W ( 2 ) W^{(2)} W(2) | 隐藏层与输出层间的权值矩阵W2 |
| y ^ \hat{y} y^ | 估计值或预测值 |
上面得到 y ^ \hat{y} y^ 只是将随机数送入神经网络后得出来的一个初始预测值,接下来我们为了使得预测能够更加准确,需要对神经网络进行训练

1.1.2 梯度下降(Gradient Descent) and 反向传播(Back Propagation)
Backpropagation and Gradient Descent are two different methods that form a powerful combination in the learning process of neural networks.Backpropagation and gradient descent work together to help a neural network learn.
训练神经网络的本质:Minimizing a Cost Function
真实值与预测值之间一定存在误差,我们通过计算真实值与预测值的均方差来构建一个函数,随后利用梯度下降法,找到函数最小值,已达到对已知样本的最优拟合
接着我们来看一看此例中该如何训练神经网络,也就是如何最小化代价函数
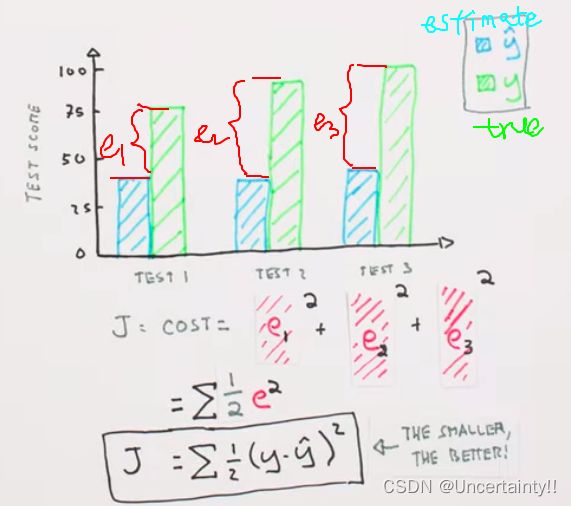
我们的目的是通过训练不断调节各个权值,从中找到的一组权值使得总体误差最小
我们先对其中一个权重矩阵W1进行尝试,对矩阵W1赋予各种值,看看代价函数costs最终会不会有个最小值
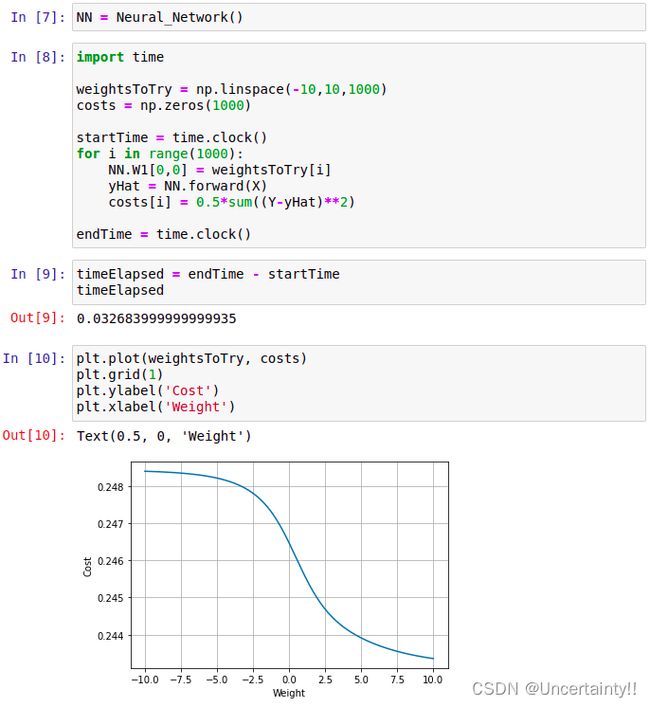
显然上述方式属于蛮力,如果对3个权重矩阵进行尝试,那么运行时间会大到可怕! 我们开始审视代价函数,从代价函数入手进行处理,通过对代价函数进行求导来找到使得代价函数减小的方式


如果代价函数是下图中的非凸函数,我们该如何防止陷入局部最优?这个问题以后再来学习,但要清楚我们需要的是全局最优,而非局部最优

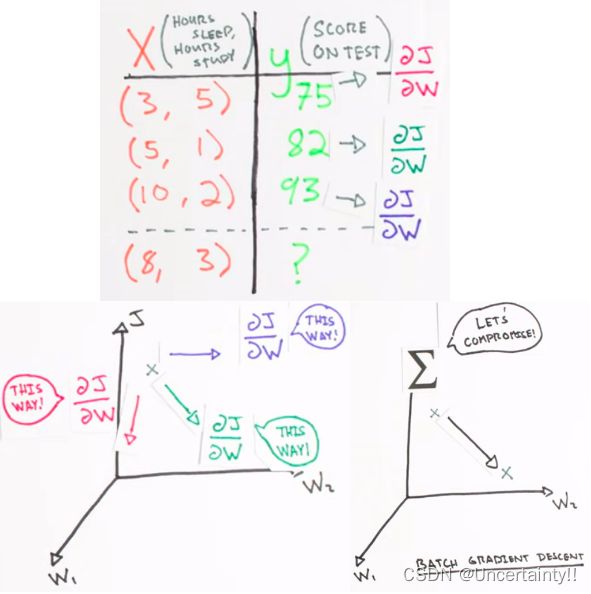


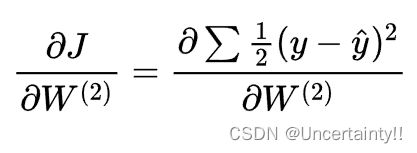 由导数法则,将加和提出,先求导后求加不影响结果
由导数法则,将加和提出,先求导后求加不影响结果
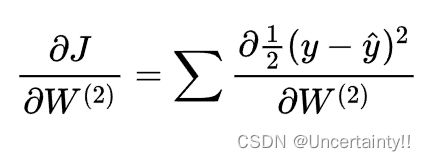
由于求和的导数等于导数的和,所以我们先暂时不考虑加和,应用链式法则求导
反向传播的一个更好名称可能是:永远不要停止执行链式法则
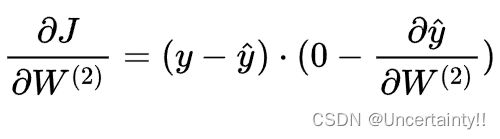
 将 y ^ = f ( z ( 3 ) ) \hat{y}=f(z^{(3)}) y^=f(z(3)) 代入上式
将 y ^ = f ( z ( 3 ) ) \hat{y}=f(z^{(3)}) y^=f(z(3)) 代入上式
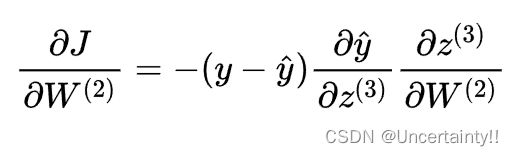 因为这里的 f 为Sigmoid,所以我们需要对Sigmoid求导
因为这里的 f 为Sigmoid,所以我们需要对Sigmoid求导
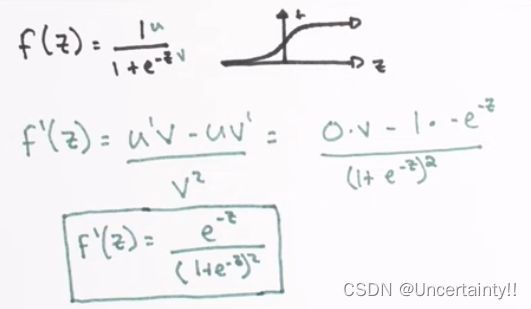
定义Sigmoid的导函数(Sigmoid Prime)

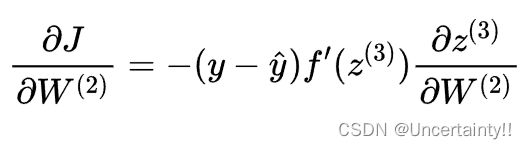



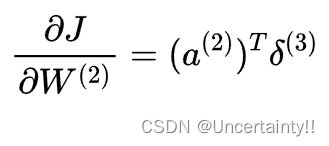 δ ( 3 ) \delta^{(3)} δ(3)是反向传播误差
δ ( 3 ) \delta^{(3)} δ(3)是反向传播误差
关于 J J J对权值矩阵W1的偏导,处理方法类似


运行后求出
∂ J ∂ W ( 1 ) and ∂ J ∂ W ( 2 ) \frac{\partial J}{\partial W^{(1)}}\ \text{and}\ \frac{\partial J}{\partial W^{(2)}} ∂W(1)∂J and ∂W(2)∂J
 如果将W1加上一个标量乘以dJW1,我们就会发现我们的代价会增加
如果将W1加上一个标量乘以dJW1,我们就会发现我们的代价会增加
(W1加上一个标量乘以dJW1似乎是在原来基础上升几个梯度的意思)
 如果将W1减去一个标量乘以dJW1,我们就会发现我们的代价会减少
如果将W1减去一个标量乘以dJW1,我们就会发现我们的代价会减少
(W1减去一个标量乘以dJW1似乎是在原来基础下降几个梯度的意思)
![]() 这也是梯度下降的核心!
这也是梯度下降的核心!
反向传播(Back Propagation Checking)
In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually
The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule
Backpropagation is an algorithm used in machine learning that works by calculating the gradient of the loss function, which points us in the direction of the value that minimizes the loss function. It relies on the chain rule of calculus to calculate the gradient backward through the layers of a neural network. Using gradient descent, we can iteratively move closer to the minimum value by taking small steps in the direction given by the gradient.
1.1.3 数值梯度检验(Numerical Gradient Checking)
神经网络没有一个好的方法来发现自己出现了问题,所以我们需要进行检验,以便神经网络的性能随着时间推移而逐步下降
如果检验的结果与神经网络得出的结果相差不大,那证明该神经网络性能良好
举个例子来简单了解一下检验的基本原理
一个是通过求导公式计算
一个是通过导数定义的公式,自己确定一个 ϵ \epsilon ϵ代入导数定义的公式进行计算
通过导数定义公式计算出的结果来验证通过求导公式计算出的结果
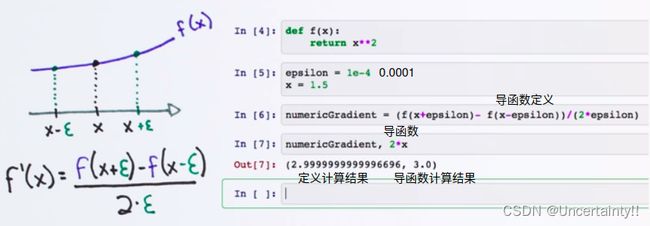 对每个权重加上一个扰动项e(perturb) ,并计算加上扰动项后的代价函数的值
对每个权重加上一个扰动项e(perturb) ,并计算加上扰动项后的代价函数的值
对每个权重减去一个扰动项e(perturb) ,并计算减去扰动项后的代价函数的值
然后计算上述两个值之间的斜率,对所有权重值重复此过程,完成后,我们得到一个数值梯度向量,此向量中的各个值,与各个对应的权重相同

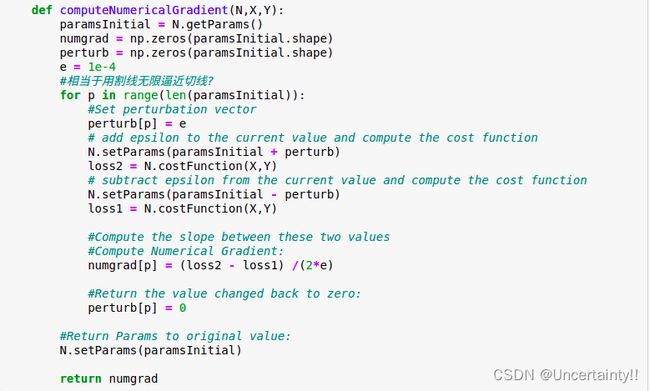
NumericalGradient是通过添加扰动项计算的结果
computerGradient是通过求导公式直接计算的结果
发现二者差别并不大,我们最后通过范数来量化一下这两个结果的相似程度

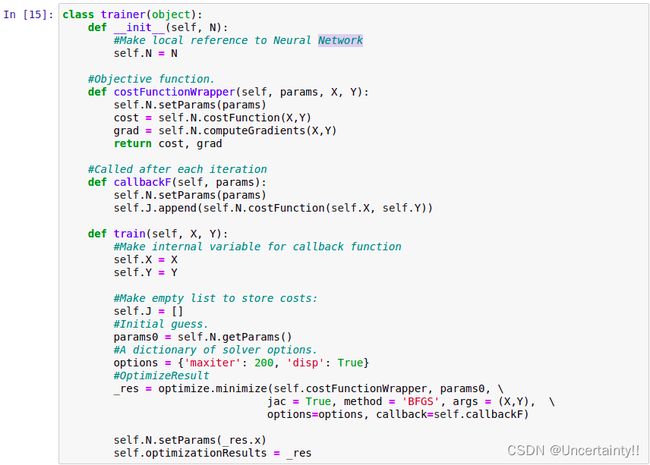
1.2 训练神经网络
我们使用梯度下降来训练神经网络
梯度下降会遇到的问题:陷入局部最优、无法找到最优值、接近最优值的速度太慢、跳过最优值等.实际问题大多数是高维情况